Понятие простых и многомерных систем, используемое в теории управления кратко

Привет, Вы узнаете о том , что такое многомерная система, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое многомерная система , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

В теории управления техническими системами часто бывает удобно систему разделить на набор звеньев, соединенных в сетевые структуры. В простейшем случае система содержит одно звено, на вход которого подается входной воздействие (вход), на входе получается отклик системы (выход).

В теории Управления Техническими Системам используют 2 основных способа представления звеньев систем управления:

— в переменных “вход-выход”;

— в переменных состояния (более подробно см. разделы 6…7).

Представление в переменных “вход-выход” обычно используется для описания относительно простых систем, имеющих один “вход” (одно управляющее воздействие) и один “выход” (одна регулируемая величина, см. рисунок 1.2.1).

Рис. 1.2.1 – Схематическое представление простой системы управления

Обычно такое описание используется для технически несложных САУ (систем автоматического управления).

В последнее время широкое распространение имеет представление в переменных состояния, особенно для технически сложных систем, в том числе и для многомерных САУ. На рис. 1.2.2 приведено схематичное представление многомерной системы автоматического управления, где u1(t)…um(t) — управляющие воздействия (вектор управления), y1(t)…yp(t) — регулируемые параметры САУ (вектор выхода).

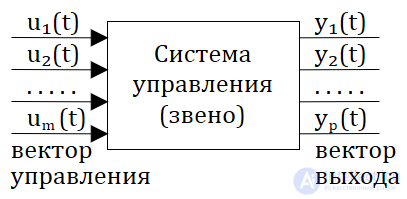
Рис. 1.2.2 — Схематическое представление многомерной системы управленияя

Рассмотрим более детально структуру САУ, представленную в переменных “вход-выход” и имеющую один вход (входное или задающее, или управляющее воздействие) и один выход (выходное воздействие или управляемая (или регулируемая) переменная).

Предположим, что структурная схема такой САУ состоит из некоторого числа элементов (звеньев). Группируя звенья по функциональному принципу (что звенья делают), структурную схему САУ можно привести к следующему типовому виду:

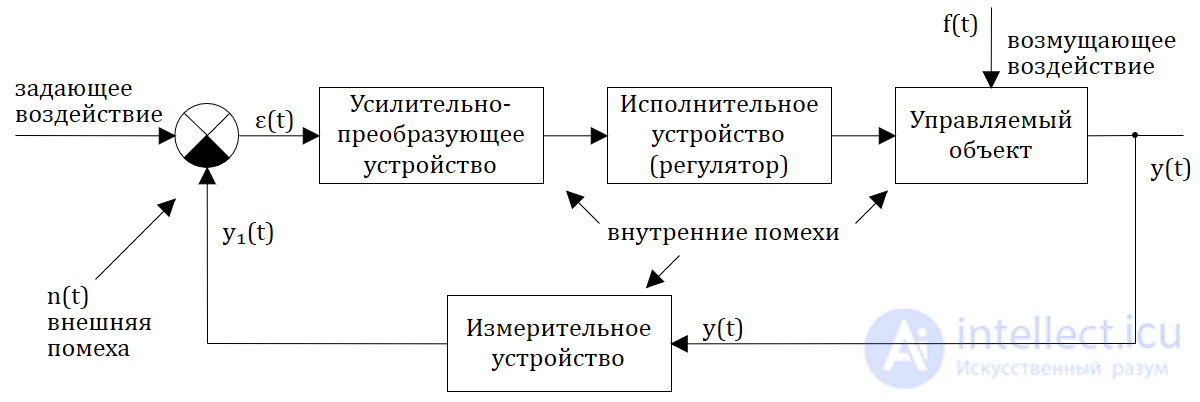
Рис. 1.2.3 — Структурная схема системы автоматического управления

Символом ε(t) или переменной ε(t) обозначается рассогласование (ошибка) на выходе сравнивающего устройства, которое может “работать” в режиме как простых сравнительных арифметических операций (чаще всего вычитание, реже сложение), так и более сложных сравнительных операций (процедур).

Так как y1(t) = y(t)*k1, где k1 — коэффициент усиления, то ==>
ε(t) = x(t) — y1(t) = x(t) — k1*y(t)

Задача системы управления состоит в том (если она устойчива), чтобы “работать” на уничтожение рассогласования (ошибки) ε(t), т.е. ==> ε(t) → 0.

Следует отметить, что на систему управления действуют как внешние воздействия (управляющее, возмущающее, помехи), так и внутренние помехи. Помеха отличается от воздействия стохастичностью (случайностью) своего существования, тогда как воздействие почти всегда детерминировано.

Для обозначения управляющего (задающего воздействие) будем использовать либо x(t), либо u(t).

Рассмотрим определение многомерной системы, используемое в теории управления.

Многомерными системами называют системы управления, в которых имеются несколько, больше одной, управляемых переменных величин.

Одномерная система характеризуется тем, что контролируется (измеряется, регулируется) лишь одна переменная величина объекта управления. Об этом говорит сайт https://intellect.icu . Рассмотрим структуру типичной одномерной системы управления на примере управления скоростью вращения электродвигателя.

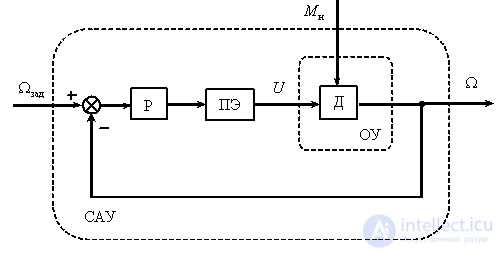
Рис. 1

В системе, показанной на рис. 1 объектом управления (ОУ) является электродвигатель (Д). На двигатель воздействует преобразователь энергии (ПЭ), приводящий двигатель в движение и изменяющий скорость посредством величины напряжения (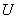), подводимого к двигателю. На двигатель так же воздействует рабочая нагрузка, создающая на валу двигателя момент (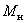), приводящий к изменению скорости (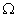) в отличие от заданной скорости (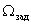). В процессе работы двигателя, при изменении нагрузки будет меняться и скорость, что является недопустимым с точки зрения требований к качеству выпускаемой продукции, на пример, скорость подачи металлорежущего станка. В функции отклонения скорости от задания регулятор (Р) воздействует на преобразователь энергии таким образом, чтобы снизить отклонение скорости.

В этом случае, как система управления в целом, так и объект управления, представляются в виде математической модели, имеющей скалярные вход, выход и возмущающее воздействие.

Для анализа и синтеза в таких системах используют математические модели в виде дифференциальных уравнений, передаточных функций, структурной схемы, частотных и временных характеристик, которые были рассмотрены в нашем курсе ранее.

Общая тенденция развития промышленных устройств состоит в повышении качества и снижении затрат. При повышении качества управления приходится учитывать большее число возмущающих факторов и требуется управлять несколькими переменными объекта. Это должно обеспечивать требования к точности, динамичности, стабильности и экономичности процесса движения вала двигателя. Тогда и объект управления (двигатель) и система управления рассматривается как многомерные.

Структура системы управления скоростью двигателя принимает вид, показанный на рис. 2.

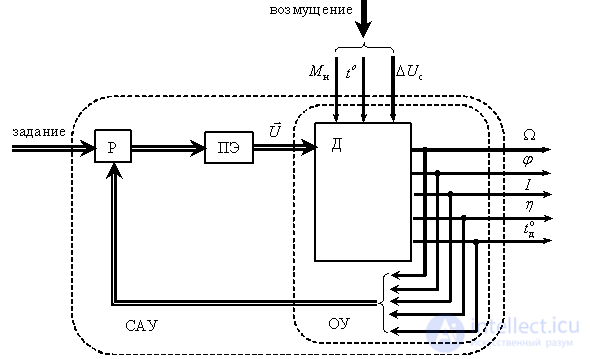
Рис. 2

Как мы видим здесь в качестве контролируемых переменных двигателя не только скорость, но и угол поворота вала 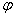, что часто требуется при точном останове вала. Также контролируют нагрузку двигателя по потребляемому току 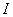, экономичность по коэффициенту полезного действия 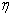, нагрев двигателя по температуре двигателя 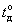. На систему действует возмущение, имеющее так же несколько компонент: момент нагрузки, температура окружающей среды 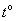, что важно для установок, работающих на открытом воздухе, и отклонение параметров питающего преобразователь энергии источника энергии, что важно для автономных установок. В этом случае управляющее воздействие на двигатель так же является векторной величиной 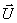. И таким образом обстоит дело не только в системах электропривода, но и в целом, при разработке систем автоматизации промышленных установок.

Во многих случаях разработки промышленных установок решается задача обеспечения заданного качества технологического процесса при минимизации энергетических и экономических затрат. При этом необходимо не только учитывать многочисленные возмущающие объект управления факторы, но и использовать несколько точек приложения управляющих воздействий.

Рассмотрим наиболее характерные примеры многомерных систем в различных отраслях промышленности.

На рис. 3 показана примерная структура установки, которая реализует процесс обработки гибких материалов. Такая структура является характерной для обработки таких материалов, как нить, проволока, ткань, тонколистовой металл, пленки, многослойные материалы.

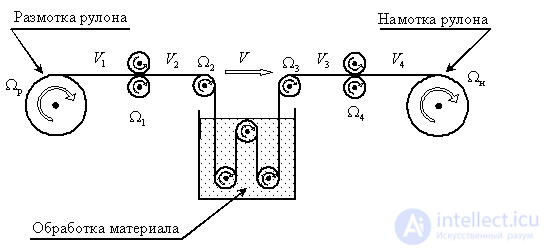
Рис. 3

Основная задача таких систем – это стабилизация скорости обработки материала 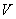с обеспечением отсутствия деформации материала. Для этого максимальное количество вращающихся роликов оснащают регулируемыми приводами, чтобы с помощью управляющих воздействий – соотношений скоростей 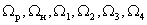, воздействовать на линейные скорости 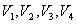, а тем самым и на другие параметры обрабатываемого материала, особенно это важно в тех случаях, когда материал является легко деформируемым, на пример, обработка марли или бинтов в текстильной промышленности.

На рис. 4 показана типичная кинематическая схема промышленного робота для манипулирования и транспортирования предметов.

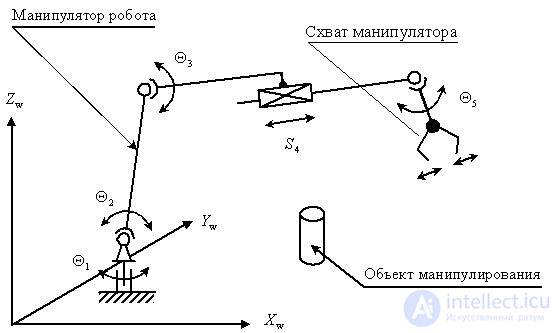
Рис. 4

Основная задача таких систем перемещение схвата манипулятора в заданную точку пространства рабочей зоны робота (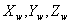 ). Эту задачу можно реализовать, воздействуя на величины углов поворота и перемещения в сочленениях манипулятора (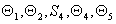), с помощью электромеханических, пневматических или гидравлических приводов.

Таким образом, здесь также мы имеем объект и систему с большим числом входных воздействий, то есть многомерную систему.

Обобщенная структура таких многомерных систем будет иметь вид, показанный на рис. 5.

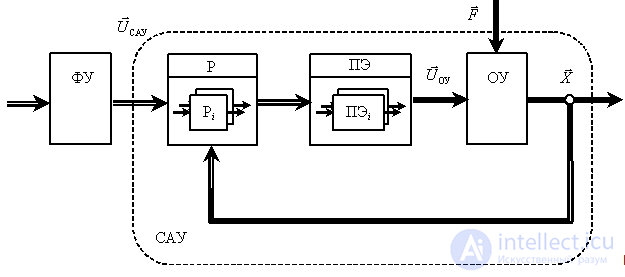
Рис. 5

Блок формирования управления (ФУ) преобразует задания оператора в вектор управления системой 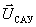. Блок регуляторов (Р), действующий в функции отклонений измеренных регулируемых величин 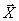от заданных, управляет преобразователями энергии (ПЭ), которые осуществляют управляющие воздействия 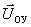на объект управления (ОУ). На объект управления действуют возмущающие воздействия .

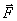Мы видим, что в этом случае многомерная система имеет векторный характер входов, выходов и возмущающих воздействий, что хорошо иллюстрирует рис. 6.

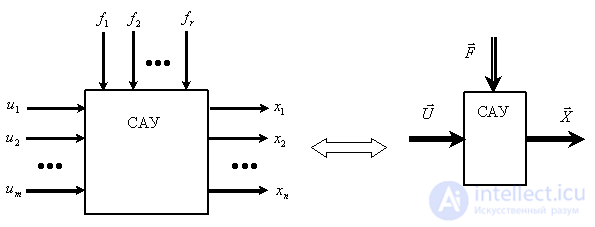
Рис. 6

На рис. 6 показаны векторы –

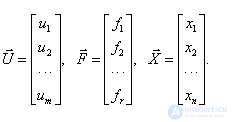
Как и в случае с одномерными (скалярными) системами ограничимся рассмотрением линейных систем управления.

Многомерные системы и объекты управления называют линейными и стационарными, если они описываются системой линейных дифференциальных уравнений с постоянными коэффициентами.

В настоящее время в практике анализа и синтеза многомерных систем сложились два подхода к проблеме получения математической модели таких систем.

Первый подход

Многомерная система рассматривается, как многосвязная совокупность динамических звеньев и представляется в виде структурной схемы или ориентированного графа.

Второй подход

Учитывая векторный характер связей между функциональными элементами САУ, при построении математических моделей используют векторно-матричное представление уравнений и структурных схем, описывающих объект управления или систему в целом.

В рамках этого подхода существует деление математических моделей на две группы.

Математические модели в частотной области

Они базируются на операторной форме представления уравнений и использовании преобразования Лапласа. Это таки модели как

• матричные структурные схемы,

• передаточные матрицы, которые иногда называют эквивалентными матрицами или матрицы "вход-выход".

Математические модели во временной области

Они базируются на векторно-матричной форме представления систем линейных дифференциальных уравнений первого порядка, широком использовании понятий и методов теории пространства состояний.

Контрольные вопросы и задачи

1. Какую систему автоматического управления или объект управления называют многомерными?

2. Какие многомерные системы называют линейными стационарными?

3. Какова размерность вектора регулируемых переменных манипулятора промышленного робота, показанного на рис. 4, с точки зрения обобщенной структуры многомерных систем, показанной на рис. 5?

4. Какие модели многомерных объектов или систем управления относят к моделям во временной области?

5. Какие модели многомерных объектов или систем управления относят к моделям в частотной области?

Вау!! 😲 Ты еще не читал? Это зря!

• Система
• Основные законы управления

Прочтение данной статьи про многомерная система позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое многомерная система и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.