4.3 Принципы управления, модели регуляторов и замкнутых систем

Привет, Вы узнаете о том , что такое принципы управления модели регуляторов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое принципы управления модели регуляторов, замкнутых систем , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Напомним, что система управления состоит из двух основных блоков, (см. введение и рис. 4.7): объекта управления (представленного управляемым процессом, измерительными и исполнительными устройствами, см. например п. 4.1) и устройством управления, которое выполняет вычислительные функции, т.е. по определенным правилам (алгоритмам) осуществляет обработку текущей информации об объекте и определяет управляющее воздействие u(t). Алгоритмы работы этого устройства зависят от динамических свойств ОУ и конкретных задач, решаемых системой. Работа системы управления происходит во взаимодействии с внешней средой, которая оказывает возмущающее влияние на движение ОУ (сигнал f (t )), а также может выступать в роли внешнего задающего блока (см. п. 4.2).

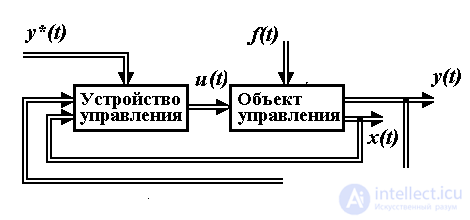
Рис. 4.7. Структура системы автоматического управления

Системы управления локального уровня обеспечивают решение задач стабилизации, слежения, терминального управления и т.д. (см. п. 1.4.1), что предусматривает поддержание заданных законов изменения регулируемых переменных y(t ) или переменных состояния x_i(t ). Управление, обеспечивающее решение локальных задач, осуществляется с помощью регулятора и задающего блока. Регулятор производит расчет управляющих сигналов САУ на основании анализа текущих значений выходных переменных y(t ) и/или переменных состояния x_i(t ), а также соответствующих задающих воздействий y*(t ) и/или x_i*(t ), поступающих от внешней среды или генерируемых задающим блоком (см. п. 4.2).

4.3.1. Принципы управления. С помощью регуляторов в систему управления вводятся контуры прямых и обратных связей. В зависимости от структуры связей имеет место классификация принципов управления, приведенная на рис. 4.8.

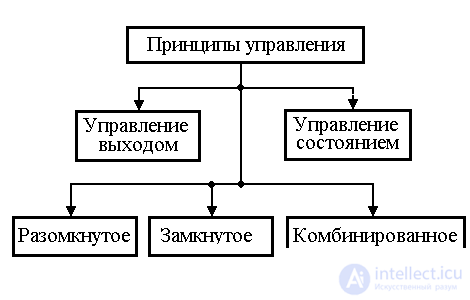
Рис. 4.8. Принципы управления

Попытка непосредственного решения локальных задач приводит к управлению по выходу ОУ и простейшей (классической) структуре САУ, содержащей контуры прямых связей по задающему воздействию у* и обратных связей по выходу у. При этом различают разомкнутое, замкнутое и комбинированное управления. Последнии два типа предусматривают наличие обратных связей по отклонению.

Разомкнутое управление вводит в состав системы контур прямой связи по задающему воздействию:

(4.68)                     u= U ( y*),

где U(·) - функциональный оператор. Управляющее воздействие рассчитывается из условия получения заданного закона изменения выхода (задающего воздействия y*(t)), а текущее поведение ОУ не контролируется. Отличие свойств реального объекта от его математической модели, используемой при построении алгоритма (4.68), возможная неустойчивость ОУ и влияние возмущений , обычно приводят к неидентичности выхода y(t ) и задающего воздействия y*(t), т.е. ошибкам разомкнутых систем управления ( см. п. 2.3.2 ).

Управление по отклонению вводит в структуру системы контур обратных связей:

(4.69)                     u = K ( ),

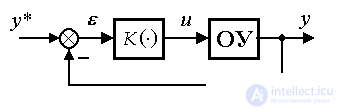
где рассогласование (отклонение)  рассчитывается по формуле:

(4.70)                     = y*- y,

а оператор K (·) выбирается из условия уменьшения отклонения  (t) в процессе работы системы. Так как в данном случае поведение ОУ корректируется в зависимости от текущего значения  , то управление по отклонению обеспечивает устойчивость системы и уменьшение влияния возмущений (см. п. 2.3.2 ).

Абсолютная точность решения задачи управления может быть достигнута с помощью комбинированного управления, предусматривающего использование как прямых, так и обратных связей :

(4.71)                     u = U(y*)+K(  ).

В ряде случаев структура системы дополняется также контурами управления по возмущающему воздействию f, что обеспечивает компенсацию возмущающего влияния внешней среды.

Системы управления одноканальными объектами, построенные по классическим принципам управления по выходной переменной, содержат не более одного контура обратной связи и поэтому условно относятся к одноконтурным системам .

Подключение дополнительных контуров обратной связи в многоконтурных системах обеспечивает повышение качества управления. Наиболее полная информация об управляемом процессе содержится в переменных состояния (см. п. 3.1.1), и поэтому управление по состоянию позволяет достичь наилучших качественных показателей системы управления.

При управлении по состоянию, также как и управлении по выходу, различают разомкнутые алгоритмы вида

(4.72)                     u= U ( x*),

представляющие контуры прямых связей по задающему воздействию x*(t), замкнутые алгоритмы управления (контуры обратных связей по отклонению):

(4.73)                     u = K (e),

где вектор рассогласований (отклонений ) e рассчитывается по формуле:

(4.74)                     e = x*- x,

и алгоритмы комбинированного типа :

(4.75)                    u = U (x*)+ K (e).

Основным функциональным элементом устройства управления является регулятор. В соответствии с рассмотренными принципами управления (см. рис. 4.8) различают регуляторы выхода и состояния, разомкнутые регуляторы и регуляторы комбинированного типа. В зависимости от функциональных операторов U ( )и K ( ), встречающихся в алгоритмах (4.68) - (4.71) или (4.72) - (4.75), различают:

• л инейные и нелинейные регуляторы ;
• регуляторы с постоянными и переменными параметрами.

Дальнейшее изложение касается только линейных регуляторов и, соответственно , линейных замкнутых систем управления.

Для описания отдельных блоков системы используются дифференциальные и операторные уравнения. Модели системы в целом находятся как объединение блоков с использованием известных правил преобразования (в том числе методов преобразования передаточных функций, см. п. 2.4.1) и могут быть получены в

• операторном виде, соответствующем описанию вход-выход;
• в виде скалярных или векторно-матричных дифференциальных уравнений - моделей вход-состояние-выход.

4.3.2. Регуляторы выхода и модели одноконтурных систем. Одноконтурная система - простейший и самый распространенный тип систем, обеспечиващих управление выходной переменной одноканального ОУ. В состав устройства управления одноконтурной САУ входит задающий блок ЗБ и регулятор выхода Р (рис. 4.9). Задача системы заключается в минимизации отклонения  = у* - у, чему препятствует возмущение f(t ) и ненулевые начальные рассогласования  (0) = ₀ . Задача решается с помощью регуляторов выхода.

Рис.4.9. Одноконтурная система

Рассмотрим свойства систем управления линейным объектом, описываемым операторным уравнением

(4.76)                      ,

где W _О (p) - передаточная функция ОУ, с различными типами регуляторов выхода.

Регуляторы разомкнутого типа представлены контуром прямой связи по задающему воздействию, т.е. алгоритмом

(4.77)                      ,

где р =d/dt - оператор дифференцирования, 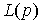 - интегро-дифференциальный оператор (передаточная функция регулятора). После подстановки (4.76) в (4.77) получаем уравнение вида

(4.78)                      ,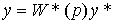

где W*(p) - передаточная функция разомкнутой системы

(4.79)                     .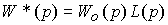

Введем в рассмотрение ошибку слежения (4.70) и подставив (4.70) в (4.78), получим уравнение, связывающее задающее воздействие y* и ошибку " (модель ошибки):

(4.80)                      .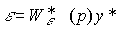

Интегро-дифференциальный оператор

(4.81)                     

называется передаточной функцией (разомкнутой системы) по ошибке слежения. Выбирая передаточную функцию регулятора как

(4.82)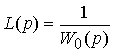                     

получим  =0 и, следовательно,

(4.83)                     y(t)=y*(t).

Таким образом, соответствующий выбор структуры регулятора (4.77) позволяет обеспечить абсолютную точность решения задачи слежения. Недостатки разомкнутых систем указаны в п. 4.3.1 и, кроме того, связаны с трудностями практической реализации оператора (4.82).

Замкнутые регуляторы ( регуляторы отклонения) вводят в состав системы обратную связь по рассогласованию 

(4.84)                      ,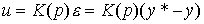

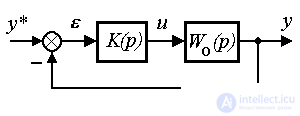
где  - интегро-дифференциальный оператор обратной связи (передаточная функция регулятора). Об этом говорит сайт https://intellect.icu . Подставляя (4.84) в уравнение ОУ (4.76), после простейших преобразований получаем уравнение замкнутой системы

(4.85)                     

или

(4.86)                      ,

где W(p) - передаточная функция разомкнутой части системы

(4.87)                     .

Уравнение (4.87) можно записать в виде (см. п. 2.4.2)

(4.88)                      ,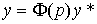

где 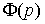 - передаточная функция замкнутой системы

(4.89)                      .

Подставляя (4.86) в уравнение (4.70) нетрудно получить модель ошибки слежения

(4.90)                     

или

(4.91)                      ,

где 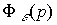 - передаточная функция замкнутой системы по ошибке слежения

(4.92)                      .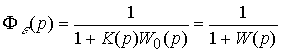

Отметим, (см. также п. 2.4.2) что замыкание системы приводит к изменению ее передаточной функции (ср. выражения (4.76) и (4.92)) и, следовательно, динамических свойств и точностных показателей.

В зависимости от частной реализации оператора  различают пропорциональные (П), пропорционально-дифференциальные (ПД), пропорционально-интегральные (ПИ) и пропорционально-интегрально-дифференциальные (ПИД) регуляторы (см. также п. 1.5.1 ):

П-регуляторы описываются алгебраическим уравнением:

(4.93)                      ,

где К_р - постоянный коэффициент обратной связи. Значение К_р выбирается таким образом, чтобы уменьшить величину отклонения  , вызванного действием возмущения f(t), начальным рассогласованием  ₀, и, возможно, высоким темпом изменения задающего воздействия у* (t). Увеличение К_р обычно обеспечивает снижение ошибки (см. выражения (4.89) и (4.92) при K(p)=K _р ) ), но приводит к ухудшению динамических свойств системы - повышению колебательности. Поэтому задача выбора коэффициента обратной связи решается компромиссным образом.

Для улучшения динамических свойств САУ (снижения колебательности) в закон управления вводят производные от отклонения  . Тем самым формируется алгоритм ПД-регулятора :

(4.94)                     ,

т.е. регулятора с передаточной функцией

(4.95)                      ,

где К_д - коэффициент обратной связи по скорости изменения ошибки  (t). Дифференциальная составляющая алгоритма (4.94) препятствует быстрым движениям ОУ и демпфирует колебания. В то же время значительное увеличение коэффициента замедляет переходные процессы и, следовательно, ухудшает динамику системы управления.

Повышение точности САУ (снижение установившейся ошибки  ) достигается при использовании ПИ-регулятора :

(4.96)                    

с передаточной функцией

(4.97)                     ,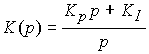

где K_I - коэффициент обратной связи по интегралу от ошибки. Интегральная составляющая алгоритма (4.96) со временем накапливает информацию об отклонении  , вызванным влиянием возмущения f и быстрым изменением задания у* (t ), и тем самым обеспечивает компенсацию возможной установившейся ошибки  _у . Увеличение коэффициента К _I ускоряет процессы накопления и компенсации, но обычно приводит к колебаниям системы.

Одновременное улучшение динамических свойств и точности САУ обеспечивается ПИД-регулятором :

(4.98)                       

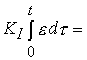
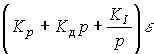
с передаточной функцией

(4.99)                      ,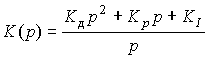

а также более сложными типами линейных регуляторов выхода (4.84).

Применение регуляторов отклонения ограничивается рядом отрицательных факторов. Во-первых, использование операции дифференцирования сопряжено с усилением помех измерения и "зашумлением" канала управления. Во-вторых, компенсация возмущающего влияния внешних воздействий f и у* требует определенных временных затрат. В третьих, для задач терминального управления (см. п. 1.4.1), в которых начальные значения отклонения  велики, управляющие воздействия принимают недопустимо большие значения.

Более эффективный метод повышения точности САУ предлагают линейные регуляторы комбинированного типа, содержащие кроме обратных связей по отклонению прямые связи по задающему воздействию:

(4.100)                      ,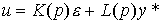

а также связи по возмущающему воздействию (рис. 4.10):

(4.101)                      ,

Рис. 4.10. Система комбинированного управления выходом

где L( р ) и L _f (p ) - интегродифференциальные операторы прямых связей.

Подставляя уравнение регулятора (4.100) в (4.76), находим уравнение замкнутой системы с комбинированным управлением

(4.102)                     

или уравнение (4.88), где передаточная функция 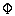 (p ) принимает вид

(4.103)                      .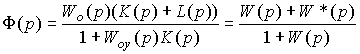

Уравнение ошибки слежения находится как

(4.104)                     

или в форме (4.91), где передаточная функция 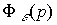 замкнутой системы по ошибке слежения находится как:

(4.105)                      .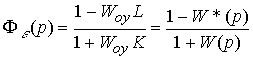

Выбор операторов прямых связей L( р ) ( и L_f (p)) осуществляется из условия компенсации возмущающего влияния задающего воздействия у* ( и при необходимости возмущения f ) . При

(4.106)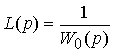                     

как и в случае разомкнутой системы получим  =0 и, следовательно,

                   

y(t)=y*(t).

Таким образом, дополнение системы прямыми связями обеспечивает абсолютную точность ее работы (  = 0), а в функцию обратных связей (составляющей 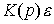 ) входит обеспечение заданных динамических свойств переходного процесса. При этом исчезает необходимость в подключении интегральных составляющих управления и оператор  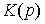выбирается как оператор П- или ПД-регулятора.

Итак, модели одноконтурных систем легко получаются в операторном виде методами преобразования передаточных функций. Для невозмущенных моделей ( f(t) = 0) - это выражения (4.102) или (4.104). Аналогичные модели могут быть получены для систем с возмущением (см. п. 2.1.4).

4.3.3. Регуляторы и модели систем управления состоянием. Системы с регуляторами состояния относятся к многоконтурным системам и, следовательно, обладают лучшими точностными и динамическими свойствами, чем одноконтурные. Они используются для управления как одноканальными, так и многоканальными ОУ. Проанализируем системы с линейными регуляторами состояния в одноканальных задачах стабилизации и слежения (см. п. 1.4.1). В общем случае в состав модели ВСВ входит следующие блоки:

Рис. 4.11. Система управления состоянием

• модель ОУ:

(4.107)                      ,

(4.108)                      ;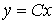

• задающий блок ЗБ (генератор задающего воздействия)

(4.109)                      ,

(4.110)                      ;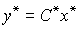

• модель внешней среды ВС (генератор возмущающего воздействия)

(4.111)                      ,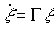

(4.112)                      ;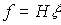

• регулятор Р, представленный одной из общих моделей вида (4.72), (4.73), (4.75).

Рассмотрим системы с наиболее распространненными типами регуляторов состояния.

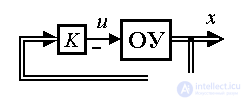
Сначала проанализируем задачу стабилизации ОУ в точке x=x*=0. Простейший регулятор состояния - пропорциональный (П-регулятор состояния, или модальный) регулятор - вводит обратные связи по переменным x_i . Алгоритм его работы описывается алгебраическим уравнением

(4.113)                      ,

где K - матрица-строка коэффициентов обратной связи

                    K= .

Алгоритм (4.113) можно записать в развернутой форме

(4.114)                      .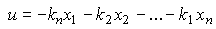

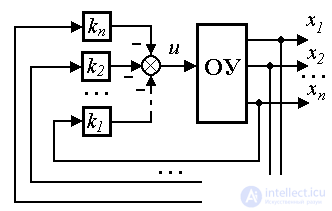
Выбор коэффициентов k_i матрицы обратных связей K обеспечивает получение заданных динамических свойств системы: быстродействия и колебательности.

Замечание 4.2. Для одноканального ОУ в качестве координат х _i вектора х можно выбрать фазовые переменные 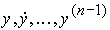 (см. 3.3). Тогда первые члены формулы (4.114) будут соответствовать описанию ПД-регулятора выхода (4.95) при задании y* = 0.

(4.115)                      .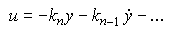

Поэтому регуляторы состояния являются обобщением ПД - регуляторов, хотя и не содержат в явном виде дифференцирующих звеньев.

Рассмотрим простейший случай задачи стабилизации ОУ

(4.116)                      ,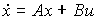

в нулевой точке: 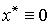 . Воспользуемся пропорциональным регулятором (4.113). Замкнутая система принимает вид

(4.117)                      ,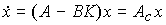

Рис. 4.12. Система с пропорциональным регулятором состояния где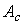
 =A-BK - матрица замкнутой системы, определяющая динамические свойства системы с пропорциональным регулятором состояния.

Отметим, что в рассматриваемом случае (при отсутствия возмущений) регулятор (4.113) обеспечивает абсолютную точность стабилизации системы в заданной точке x*=0.

Пример 4.4. Для объекта второго порядка вида

(4.118)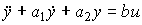                     

(см. пример 3.1) модель (4.116) принимает вид

(4.119)                      ,

(4.120)                      +bu,

(4.121)                      ,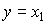

т.е.

Рис. 4.13. Система второго порядка

                    ,  ,  .

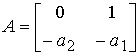Здесь пропорциональный алгоритм управления имеет вид

(4.122)                       ,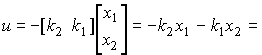

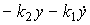т.е.

                    .

Модель замкнутой системы принимает вид

(4.123)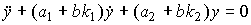                     

или (4.117), где матрица замкнутой системы находится как

                    .

В условиях действия на ОУ внешних возмущений точностные показатели системы с пропорциональным регулятором состояния ограничены. Повышение установившейся точности достигается введением в состав регулятора контуров интегральных обратных связей. ПИ-регулятор состояния реализует алгоритм:

(4.124)                      ,

где К _I - матрица коэффициентов обратной связи по интегралу от вектора состояния. Интегральная составляющая алгоритма (4.124) c течением времени обеспечивает частичную или полную компенсацию возмущения f (t).

Комбинированный регулятор состояния позволяет обеспечить компенсацию возмущения за счет прямых связей по возмущению f (t ). Отметим, что наилучшие результаты могут быть получены при использовании достаточно полной информации о возмущении, что соответствует введению прямых связей по вектору состояния внешней среды  (t):

(4.125)                      ,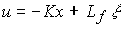

где L_f - матрица прямых связей. Во многих случаях вектор  , составлен из возмущения f и его производных.

Задача слежения рассматривается как задача отработки расширенного вектора задания x*(t ). П-регулятор состояния в подобных следящих системах вырабатывает управляющие сигналы, пропорциональные вектору отклонения е = х*-х, т.е. описывается уравнением

(4.126)                      .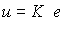

Алгоритм (4.126) можно записать в развернутой форме

(1.27)                     u= ,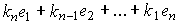

где

(4.128)                      .

Замечание 4.3. В качестве координат х _i вектора х можно выбрать фазовые переменные 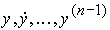 (см. замечание 4.2), а в качестве координат вектора x* - функции  . Тогда

(4.129)                     

и первые члены формулы (4.127) будут соответствовать описанию ПД-регулятора выхода (4.94):

(4.130)                      .

ПИ-регулятор состояния дополняет структуру системы интегральными связями и описывается выражением

(4.131)                      .

Интегральная составляющая алгоритма (4.131) обеспечивает c течением времени частичную или полную компенсацию возмущающего влияния задающих воздействий и возмущений.

Эффективная компенсация отклонений, вызванных возмущением f(t ) и текущими вариациями задания x*(t ), достигается при использовании комбинированного алгоритма управления (рис. 4.14)

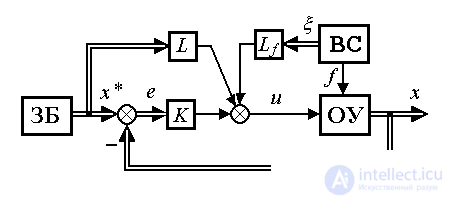
Рис. 4.14. Комбинированная система управления состоянием

(4.132)                      .

Замечание 4.4. В отличие от регуляторов выхода большинство алгоритмов управления состоянием (алгоритмы (4.113), (4.125), (4.126), (4.132)) не используют динамических операторов, что обеспечивает их более простую практическую реализацию.

Рассмотрим задачу стабилизации невозмущенного ОУ (4.116) в произвольной точке: 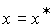 . Задача сводится к задаче слежения, где задающий блок представлен уравнением

(4.133)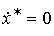                     

с начальным значением x*(0) = x* . Воспользуемся пропорциональным регулятором (4.126). Модель ошибки получается дифференцированием по времени выражения (4.74) и подстановкой уравнений (4.116) и (4.109):

(4.134)                      .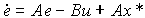

Она имеет структуру возмущенной модели (4.107), где роль возмущения играет компонента Ax* . При использовании пропорционального регулятора

(4.135)                      ,

модель ошибки (4.134) принимает вид

(4.136)                      ,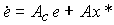

где 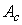 - матрица замкнутой системы. Если det A_c  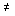0, из условия  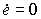получим значение уставившейся ошибки (см. п. 3.2.3)

(4.137)                     

и, следовательно, пропорциональный регулятор не обеспечивает абсолютной точности решения рассматриваемой задачи.

При использовании комбинированного регулятора

(4.138)                      ,

модель ошибки (4.134) принимает вид

(4.139)                      .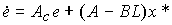

Если матрицу прямых связей L выбрать так, чтобы

(4.140)                      ,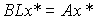

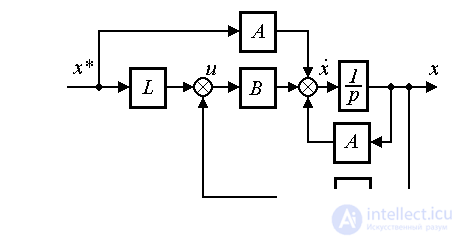
Рис. 4.115. Комбинированная система стабилизации состояния

то уравнение ошибки принимает вид

(4.141)                      .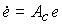

Из последнего уравнения видно, что e _у = 0 и, следовательно введение прямых связей по задающему воздействию обеспечивает в установившемся режиме абсолютную точность стабилизации

                    x=x*.

Итак, модели систем управления состоянием получаются как совокупность динамических моделей объекта управления, задающего блока, внешней среды и регулятора. Простейшие преобразования позволяют получить уравнения замкнутых моделей состояния, а при необходимости, моделей ошибок стабилизации (слежения).

Прочтение данной статьи про принципы управления модели регуляторов позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое принципы управления модели регуляторов, замкнутых систем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления