Лекция
Привет, Вы узнаете о том , что такое взаимосвязь видов ма тических моделей многомерных систем, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое взаимосвязь видов ма тических моделей многомерных систем , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Выше были рассмотрены два вида моделей многомерной системы. Установим связь между этими двумя видами. Так как исходной базой для математических моделей являются дифференциальные уравнения, то логичным будет определить связь уравнений состояния с передаточными матрицами САУ. Для этого применим преобразование Лапласа к уравнениям состояния и выхода
|
|
(1) |
|
|
(2) |
при нулевых начальных условиях, заменим оригиналы переменных изображениями по Лапласу и получим систему векторно-матричных операторных уравнений
|
|
(3) |
Определим связь между вектором входа и векторами состояния и выхода. Из первого уравнения системы (3) имеем –
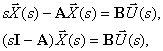
и если матрица 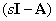 не вырожденная, то есть
не вырожденная, то есть 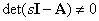 , получим –
, получим –
|
|
(4) |
Откуда следует, что
|
|
(5) |
Подставив (4) в (3), получаем –
 ,
,
В результате получаем –
|
|
(6) |
Вспомним, что компонентами эквивалентных матриц являются передаточные функции системы. Следовательно, выражения (5) и (6) представляют собой универсальные формулы для вычисления всех необходимых для анализа передаточных функций многомерной системы, по которым могут быть получены структурные схемы и частотные характеристики.
Заметим, что каждый элемент эквивалентных матриц (передаточных функций) имеет, по определению обратной матрицы, сомножитель –

То есть полином 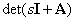 является общим знаменателем для всех передаточных функций, а уравнение –
является общим знаменателем для всех передаточных функций, а уравнение –
|
|
(7) |
является характеристическим уравнением системы.
Таким образом, мы не только получили связь между математическими моделями во временной и частотной областях, но и универсальные выражения для определения передаточных функций и характеристических уравнений любых линейных объектов или систем управления. Исходными параметрами для выражений (5),(6) и (7) являются матрицы параметров уравнений состояния и выхода. Выполнить преобразования (5),(6) и (7) можно с помощью компьютера, имеющего программы символьной математики, на пример, такие, как Mathematica 3.0 (4.0), разработанные Wolfram Research. в системах второго и третьего порядка эти преобразования можно производить и вручную.
Рассмотрим несколько примеров получения и преобразования моделей.
Пример
Рассмотрим объект, принципиальная электрическая схема которого показана на рис. 1.

Рис. 1
Выполним для этого объекта следующие задачи:
Получить уравнение состояния.
Определить характеристическое уравнение объекта.
Определить передаточную матрицу объекта.
Получение уравнения состояния
Запишем дифференциальные уравнения, описывающие процессы в схеме
|
|
(8) |
Зададим векторы состояния и входа:
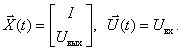
Получаем, что 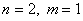 . Об этом говорит сайт https://intellect.icu . Запишем уравнение состояния в развернутой форме для нашего случая:
. Об этом говорит сайт https://intellect.icu . Запишем уравнение состояния в развернутой форме для нашего случая:
|
|
(9) |
Раскроем в (9) матричные скобки:
|
|
(10) |
Приведем систему уравнений (8) к виду (10), используя при отсутствии переменной в правых частях нулевые коэффициенты:
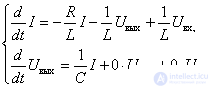
Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния
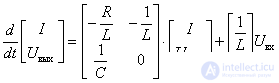 .
.
Следовательно, матрицы параметров имеют следующий вид –
|
|
(11) |
Определение характеристического уравнения объекта
Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (11), используя выражение (7) –
|
|
(12) |
Подставив в (12) выражения для матрицы параметров 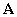 и единичной матрицы
и единичной матрицы 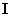 , получим характеристическое уравнение
, получим характеристическое уравнение
|
|
(13) |
Определение передаточной матрицы объекта
Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:
|
|
(14) |
Матрица 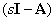 может быть определена из (13)
может быть определена из (13)
 .
.
Определим обратную матрицу, помня о том, 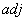 – адъюнкт исходной матрицы представляет собой транспонированную матрицу алгебраических дополнений элементов матрицы, а алгебраические дополнения определяются для каждого элемента исходной матрицы по следующему выражению –
– адъюнкт исходной матрицы представляет собой транспонированную матрицу алгебраических дополнений элементов матрицы, а алгебраические дополнения определяются для каждого элемента исходной матрицы по следующему выражению –
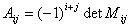 ,
,
где 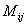 – минор исходной матрицы, полученный вычеркиванием
– минор исходной матрицы, полученный вычеркиванием 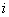 — ой строки и
— ой строки и 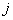 -го столбца.
-го столбца.
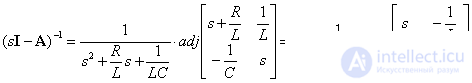 .
.
Окончательно получаем –

Следовательно, получаем передаточные функции объекта
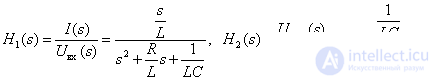 .
.
Пример
Электродвигатель постоянного тока независимого возбуждения (с постоянными магнитами) как объект управления описывается следующей системой дифференциальных уравнений –
|
|
(15) |
где 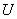 – напряжение, подаваемое на двигатель,
– напряжение, подаваемое на двигатель, 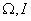 – скорость и ток двигателя,
– скорость и ток двигателя, 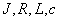 – параметры двигателя, соответственно момент инерции, сопротивление и индуктивность обмотки якоря, конструктивный коэффициент.
– параметры двигателя, соответственно момент инерции, сопротивление и индуктивность обмотки якоря, конструктивный коэффициент.
Получение уравнения состояния
Зададим векторы состояния и входа:
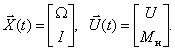
Получаем, что 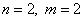 . Запишем уравнение состояния в развернутой форме для нашего случая:
. Запишем уравнение состояния в развернутой форме для нашего случая:
|
|
(16) |
Раскроем в (16) матричные скобки:
|
|
(17) |
Приведем систему уравнений (15) к виду (17), используя при отсутствии переменной в правых частях нулевые коэффициенты:
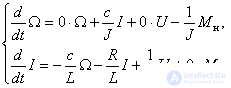
Теперь известны все компоненты матриц параметров, и можно записать уравнение состояния в развернутой форме
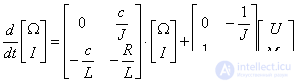 .
.
Следовательно, матрицы параметров имеют следующий вид –
|
|
(18) |
Определение характеристического уравнения объекта
Характеристическое уравнение системы определим по матрицам параметров уравнения состояния (18), используя выражение (7) –
|
|
(19) |
Подставив в (19) выражения для матрицы параметров 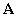 и единичной матрицы
и единичной матрицы 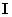 , получим характеристическое уравнение
, получим характеристическое уравнение
|
|
(20) |
Определение передаточной матрицы объекта
Определим эквивалентную матрицу передаточных функций, которая связывает векторы состояния и управления по выражению (5), которое для нашего случая имеет вид:
|
|
(21) |
Матрица 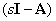 может быть определена из (20)
может быть определена из (20)
 .
.
Определим обратную матрицу –
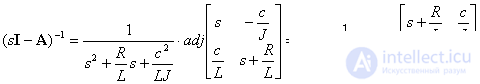 .
.
Окончательно получаем –

Следовательно, получаем передаточные функции объекта
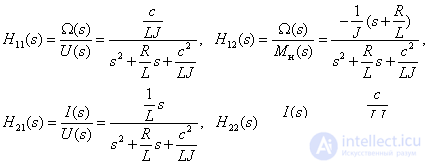
Контрольные вопросы и задачи
Поясните, как связаны между собой модели во временной и частотной области?
Как определить по уравнению состояния характеристическое уравнение?
Как определить по уравнению состояния матрицу передааточных функций системы?
По уравнению состояния
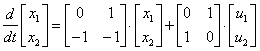 ,
,
описывающему многомерную систему, определить характеристическое уравнение системы.
Ответ:
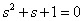 .
.
По уравнению состояния
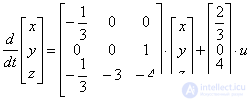 ,
,
описывающему многомерную систему, определить характеристическое уравнение системы.
Ответ:
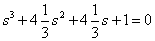 .
.
По уравнению состояния
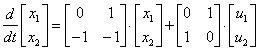 ,
,
описывающему многомерную систему, определить матрицу передаточных функций системы.
Ответ:
 .
.
Прочтение данной статьи про взаимосвязь видов ма тических моделей многомерных систем позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое взаимосвязь видов ма тических моделей многомерных систем и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про взаимосвязь видов ма тических моделей многомерных системОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления