Привет, Вы узнаете о том , что такое кибернетические понятия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кибернетические понятия, предмет теории управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

 

1.1.1. Процессы и сигналы. Динамическим процессом или движением, называется развитие во времени некоторого физического явления. К процессам относятся движения механизмов, тепловые явления, экономические процессы и т.д.

Процессы порождают информационные потоки, т.е. вторичные процессы, несущие информацию о первичном динамическом процессе. Процесс, содержащий информацию о развитии физического явления (первичном процессе) называется сигналом

При рассмотрении сигнала принято различать его информационное содержание (информацию о первичном процессе) и физическую природу соответствующего вторичного процесса (носителя). В зависимости от физической природы носителя можно выделить акустические, оптические, электрические и электромагнитные сигналы. В общем случае, природа физического носителя не совпадает с природой первичного процесса.

Замечание 1.1. Сигналы как и порождающие их процессы существуют вне зависимости от наличия измерителей или наблюдателя.

В различных областях науки и техники приняты свои определения и подходы к изучению сигналов. Рассматриваемая здесь кибернетическая трактовка этого понятия предусматривает отказ от изучения физических особенностей как первичного процесса, так и носителя сигнала. Сигнал отождествляется с информацией об изменении физических переменных изучаемого процесса. При этом учитывается, что по различным причинам реальный сигнал не содержит всей информации о развитие физического явления, а, с другой стороны, может содержать постороннюю информацию. На информационное содержание сигналов оказывают влияние способы их кодирования, шумы и эффекты квантования.

В зависимости от способа кодирования различают аналоговые и цифровые сигналы. Для аналоговых сигналов интенсивность физического носителя пропорциональна (аналогична) изучаемой физической переменной, в то время как в цифровых сигналах информация представлена в виде чисел (например, в форме параллельных и последовательных двоичных кодов).

Методы преобразования, кодирования и передачи информации специально изучаются в прикладной теории информации. В теории управления представляет интерес насколько закодированная информация адекватна рассматриваемой физической переменной. Этот вопрос связан с понятиями идеального и реального сигнала.

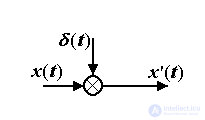
Идеальный сигнал с информационной точки зрения тождествен некоторой физической переменной x(t), в то время как реальный сигнал можно представить в виде

                   x'(t) = x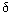(t)+ (t),

где 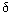 (t) - помеха измерения или шум, т.е. посторонняя информация о канале связи, внешней среде или измерителе.

С понятием реального сигнала связаны вопросы идентификации (оценивания) динамических процессов по текущим измерениям x'(t) и, в частности следующие задачи:

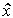• наблюдения, или получения в реальном времени оценки  (t) изучаемого процесса x(t);
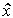• фильтрации, или получения апостериорной оценки процесса  (t-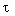 ), где  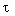- интервал запаздывания;
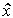• прогнозирование, или предсказания будущих значений  (t+c ).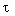

Задачи оценивания первичного процесса по реальным измерениям рассматриваются в теории оценивания (идентификации).

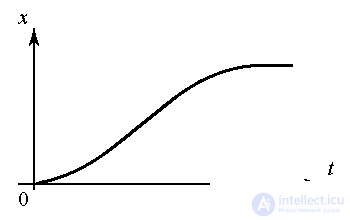
Информационное содержание сигнала зависит и от эффектов квантования. По характеру изменения во времени процессы и сигналыподразделяются на непрерывные и дискретные. К последним, в свою очередь, относятся процессы квантованные по уровню и процессы квантованные по времени.

Развитие непрерывного неквантованного) процесса характеризуется переменной x(t), принимающей произвольные значения из числовой области X и определенной в любые моменты времени t > 0. К непрерывным процессам относится непрерывное механическое движение, электрические и тепловые процессы.

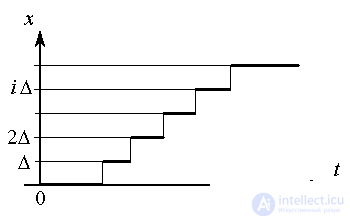
Развитие дискретного (квантованного по уровню) процесса характеризуется переменной x(t), принимающей строго фиксированные значения xⁱ , i=1,2..., и определенной в любые моменты времени t > 0. В большинстве практических случаев можно положить

                    xⁱ = i  x , i= ,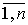

где  x - приращение или уровень дискретности, n - число допустимых состояний.

К процессам квантованным по уровню можно отнести:

• бинарные процессы (релейные процессы и двоичные сигналы), где n=2 ;
• дискретные автоматические линии;
• пневматические роботы-манипуляторы, имеющие конечное число фиксированных положений в пространстве;
• k-разрядные двоичные регистры, имеющие 2^k состояний;
• все процессы в цифровых устройствах и ЭВМ.

Замечание 1.2. В тех случаях, когда число состояний n достаточно велико или интервал дискретности  x достаточно мал, квантованием по уровню пренебрегают.

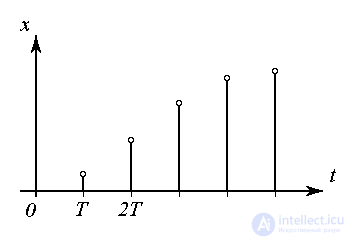
Развитие дискретного(квантованного по времени) процесса, или процесса дискретного времени, характеризуется переменной x(t) принимающей произвольные значения x и определенной в фиксированные моменты времени tⁱ ,i=0,1,2..... Во многих случаях

                    t=i T, i 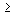 0,

где Т- интервал квантования (дискретности). К таким процессам относятся:

• экономические процессы, связанные с календарем (например, динамика курса ценных бумаг, где Т=1день);

• процессы в цифровых вычислительных устройствах, где T=1/f, f - тактовая частота процессора;
• процессы в цифровых системах управления, в которых дискретность по времени обусловлена циклическим характером обработки информации в реальном масштабе времени (здесь Т- время обновления информации на выходном регистре управляющей ЭВМ).

Замечание 1.3. При достаточно малых (по сравнению с длительностью других процессов) интервалах T дискретностью по времени пренебрегают и квантованный по времени процесс относят к процессам непрерывного времени.

Замечание 1.4. К дискретным обычно относят также кусочно-постоянные процессы и сигналы, которые характеризуются переменной x(t), скачкообразно изменяющиеся в фиксированные моменты времени tⁱ .

1.1.2. Кибернетические блоки. Кибернетический блок ("черный ящик") - это блок, для которого установлены связанные причинно-следственным отношением входные и выходные сигналы. Об этом говорит сайт https://intellect.icu . Выходной сигнал блока x₂(t) несет информацию о внутреннем процессе, причиной которого является входной сигнал x₁ (t).

Замечание 1.5. В определении блока отсутствует упоминание физической природы процессов внутри блока, что и определило термин "черный ящик".

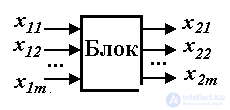
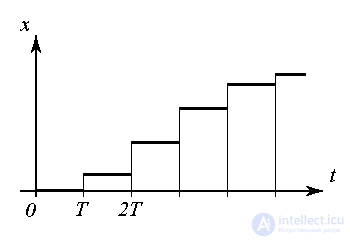
В зависимости от числа входных и выходных сигналов различают одноканальные блоки, т.е. блоки с одним входом и одним выходом, и многоканальные с несколькими входными и выходными сигналами. Блоки, у которых отсутствуют входные сигналы называются автономными. По типу сигналов различают непрерывные, дискретные и дискретно-непрерывные блоки.

Для описания кибернетического блока используется одна из форм аналитического описания связи входных и выходных сигналов. Для простейших блоков такое описание может быть получено в виде алгебраического или трансцендентного уравнения:

(1.1)                   x₂ = f(x₁),

где f (· ) - функция. В более общем случае для описания блоков используются дифференциальные и разностные (рекурентные) уравнения, автоматные алгоритмы, т.е. выражения вида

(1.2)                   x₂(t) = F(x ₁(t)),

где F(· ) - функциональный оператор.

 
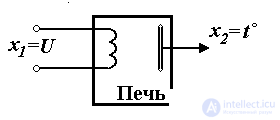
Рис. 1.1. Электронагревательная печь

Пример 1.1. Рассмотрим электронагревательную печь, т.е. камеру (рис. 1.1), температура в которой t ^o регулируется с помощью электрического нагревателя. Входным сигналом рассматриваемого блока является напряжение нагревателя: x₁(t)=U(t), а выходным - температура: x₂(t)=t^o (t). Связь выхода и входа описывается функциональным оператором (дифференциальным уравнением):

(1.3)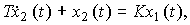                  

где T - постоянная времени, K - коэффициент передачи. Если напряжение нагревателя постоянно, т.е. x₁=U=const, то выходная переменная находится как

 .

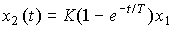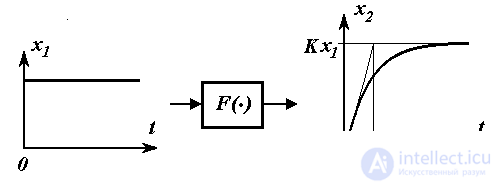
Рис. 1.2.

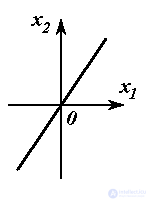
В установившемся режиме, т.е. после окончания процессов в печи при 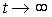 , связь выходного и входного сигналов описывается простейшим алгебраическим уравнением вида (1.1)

(1.4)                    .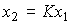

Аналогичные выражения для описания связей входных и выходных переменных получаются для электрической RC-цепи (рис. 1.3). Здесь x₁(t)=U₁(t) - входное напряжение, x₂(t)=U₂(t) - выходное напряжение схемы, T=RC и K=1.

Наконец, те же уравнения (1.1) и (1.2) описывают процесс разгона электродвигателя (рис. 1.4), для которого x₁(t)=U(t) - входное напряжение, а x₂(t)=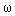 (t) - скорость вращения вала.

 

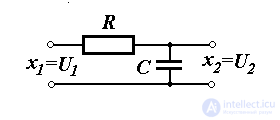
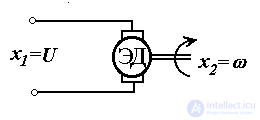
Рис. 1.3. RC - цепь          Рис. 1.4. Электродвигатель

 

С понятием кибернeтического блока связаны следующие задачи:

• идентификации, или определение аналитического выражения (связи) между сигналами x₂ и x₁;
• управления, или определение входного сигнала x₁(t), обеспечивающего получение заданного выходного сигнала x₂(t) в предположении, что описание блока известно (такая задача известна в теории дифференциальных уравнений как обратная задача Н.П. Еругина).

1.1.3. Кибернетические системы. Кибернетическая система - это упорядоченная совокупность (система) кибернетических блоков, связанных между собой информационными каналами.

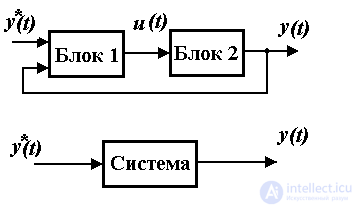
Замечание 1.6. Понятие системы предполагает появление нового качества, вообще говоря, отличного от свойств отдельных ее элементов. Связи, упомянутые в определении, носят сигнальный (информационный) характер.

Для описания системы необходимо получить аналитические зависимости, описывающие каждый из блоков (Блок 1, Блок 2 и т.д.) в отдельности и связи между ними. После эквивалентных преобразований может быть получено общее (эквивалентное) описание системы как составного кибернетического блока с входным сигналом у*(t) и выходным сигналом y(t). (см. пп. 2.4 и 4.3)

Таким образом, кибернетическая система является сложным блоком. В зависимости от числа входных и выходных сигналов различают одноканальные системы (с одним входом и одним выходом), и многоканальные системы с несколькими входными и выходными сигналами. Системы, у которых отсутствуют входные сигналы называются автономными.

По типу сигналов в системе (или блоков) различают: непрерывные, дискретные и дискретно-непрерывные системы, причем последние содержат как непрерывные, так и дискретные блоки (см. ниже).

Определение кибернетической системы позволяет ввести следующие задачи:

• анализа системы, т.е. определения связи между ее входом и выходом (в виде алгебраического или дифференциального уравнения и т.д.), а также нахождения косвенных показателей качества системы (быстродействия, точности и т.д.);
• управления (синтеза) кибернетической системы, т.е. нахождения блоков и связей между ними, обеспечивающих заданную связь входных и выходных сигналов, либо заданные качественные показатели.

Известна также прикладная задача проектирования системы, включающая в себя задачу управления (синтеза системы), ее комплектации (выбора физических элементов), разработки прикладных программ управляющих ЭВМ и т.д.

Наиболее распространенным типом дискретно-непрерываных систем являются цифровые системы, в состав которых входят цифровые вычислительные устройства (ЭВМ и цифровые контроллеры).

 

1.1.4. Дискретно-непрерывные (цифровые) системы. Рассмотрим простейшую цифровую систему управления вращением кинематического механизма (рис. 1.5). В состав системы входит простейший кинематический механизм КМ, электродвигатель ЭД, усилитель У, цифро-аналоговый преобразователь ЦАП и управляющая вычислительная машина ЭВМ.

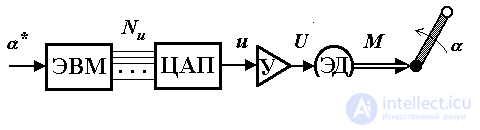
Рис. 1.5. Система управления вращением кинематического механизма

Работа системы происходит следующим образом. Информация о требуемом угле поворота (задание)  * поступает на ЭВМ, где осуществляется расчет необходимого управляющего сигнала N_u (t). Последний представлен в виде цифрового кода, который преобразуется в аналоговый управляющий сигнал u(t) c помощью цифро-аналогового преобразователя. Так как мощности полученного сигнала u(t) не достаточно для приведения в действие электродвигателя, то требуется подключения усилителя мощности У. Выходное напряжение усилителя U(t), будучи приложено к двигателю, приводит к созданию необходимого движущего момента (сигнал M(t)). Момент электродвигателя прикладывается к валу кинематического механизма и обеспечивает его вращение, т.е. изменение углового положения  (t) от начальной величины  (0) до заданного значения  *.

Отметим, что сигналы в рассмотренной системе различны по физической природе и способам кодирования. В силу дискретности процессов в цифровых вычислительных устройствах и конечности их разрядной сетки, ЭВМ относится к дискретным блокам, а сигнал на ее выходе N_u (t) является квантованным по времени и уровню.

Система, приведенная на рис. 1.5, относится к классу разомкнутых систем управления, в которых задача управления (изменения состояния КМ) решается без учета реального положения механизма  (t). Это вызывает, во-первых, определенные сложности расчета управляющего сигнала u (t), обеспечивающего заданное угловое перемещение механизма  *, а во-вторых, не позволяет гарантировать достаточной точности управления в условиях действия на механизм сил тяжести и трения. Указанные недостатки устраняются в замкнутых системах, в состав которых входит подсистема контроля и обратные связи.

Дополним рассмотренную ранее систему следующими элементами (рис. 1.6): измерительным потенциометром, выходное напряжение которого u  (t), пропорционально текущему значению  (t), усилителем У и аналого-цифровым преобразователем АЦП, осуществляющим преобразование сигнала U  (t) на выходе усилителя в цифровой код N  (t), поступающий далее на ЭВМ. Эти элементы в совокупности с ЭВМ составляют цифровую подсистему контроля вращения кинематического механизма, обеспечивающую измерение текущего положения КМ и ввод информации в управляющую вычислительную машину.

 

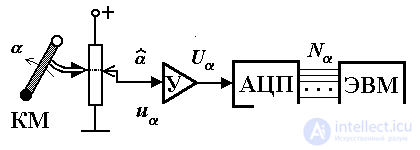
Рис. 1.6. Подсистема контроля

Отметим дискретный характер сигнала (цифрового кода)N (t), что обусловлено функциональными особенностями АЦП, и, следовательно, дискретно-непрерывный тип рассмотренной подсистемы контроля.

Объединение разомкнутой системы управления (рис. 1.5) и подсистемы контроля (рис. 1.6) позволяет получить замкнутую систему управлению. Укрупненная схема такой системы представлена на рис. 1.7. Она включает в свой состав цифровой блок управления и электро-механический блок (ЭМ блок). Последний включает аналоговые элементы системы (кинематический механизм, двигатель, усилители и измерительный потенциометр) и по типу сигналов относится к непрерывным блокам. В блок управления входит ЭВМ и устройства ввода-вывода информации (УВВ), или сопряжения с объектом (УСО), представленные цифро-аналоговыми и аналого-цифровыми преобразователями и обеспечивающие сопряжение цифровой и аналоговой частей системы управления.

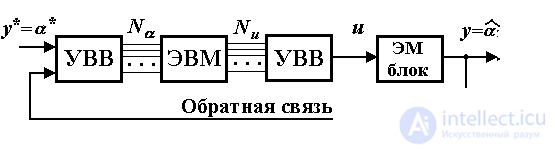
Рис. 1.7. Замкнутая система управления

 

В функции цифрового блока управления входит расчет управляющего сигнала u(t ) на основании задания  *и текущей информации о положении кинематического механизма  (t ). Простейший алгоритм расчета (пропорциональный алгоритм управления) имеет вид

(1.5)                   u(t) = K ( *- (t)),

где K - постоянный коэффициент. При расчетах по формуле (1.5) управляющий сигнал пропорционален текущему значению отклонения  *-  (t>), что обеспечивает:

• движение кинематического механизма в нужном направлении (в зависимости от знака отклонения) при,  t)   *;
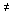
• остановку механизма при  * =  (t ) в силу u(t)= 0 и, следовательно, нулевых значений напряжения на выходе усилителя мощности U вращающего момента М .

Укрупненный алгоритм работы ЭВМ в режиме реального времени представлен на рис. 1.8. Он включает блок ввода данных (задания у* =  * и текущего значения у =  )), блок расчета текущего значения управления u по формуле (1.5) и блок вывода данных (полученного значения u ). Циклическое выполнение алгоритма обеспечивает возможность обновления выходных данных в процессе работы системы при изменения входных данных (текущего значения  ).

Циклический характер выполнения программы служит причиной временной дискретности сигналов N  и N_u и цифрового устройства управления в целом. При этом интервал квантования приближенно оценивается временем, необходимым для выполнения одного цикла программы.

Отметим, что рассмотренная система управления является составным кибернетическим блоком с входным сигналом у* =  * и выходным сигналом y=  (t ). Система содержит обратную связь по выходной переменной (сигнал у поступает обратно на вход системы). Ее аналитическое описание (связь у* и y ) можно получить на основании известных приемов преобразования динамических систем (см. пп. 2.4 и 4.3), используя описание электромеханического блока (связь сигналов y и u ) и формулу (1.5).

1.1.5. Кибернетика и предмет теории автоматического управления. Понятие кибернетики как науки об управлении и связи в живом (природе и обществе) и машинах было введено в 1948 году Норбертом Винером. В настоящее время в виде отдельных дисциплин можно выделить следующие разделы кибернетики:

• системный анализ (теория больших систем, теория сложных систем и т.д.);
• теория автоматического управления (ТАУ);
• прикладная теорию информации;
• теория оценивания (идентификации);
• теория вычислительных машин (информатика);
• робототехника и т.д.

В зависимости от области применения различают техническую кибернетику, т.е. кибернетику в технических приложениях, биокибернетику, медицинскую кибернетику, экономическую кибернетику и др.

Теория автоматического управления (ТАУ) - наука об управлении, изучающая задачи анализа и синтеза систем автоматического управления (САУ), как одного из классов кибернетических систем. Основные разделы ТАУ - это:

• анализ САУ, т.е. анализ устойчивости, структурных свойств, динамических показателей качества, точности;
• синтез САУ, т.е. синтез алгоритмов (аналитических выражений), описывающих блоки системы и их связи, и обеспечивающих заданное (может быть, оптимальное) качество управления.

Современная теория управления занимает одно из ведущих мест в технических науках и, в то же время, относится к одной из отраслей прикладной математики. Теория и практика автоматического управления связана с вычислительной техникой. В этой связи следует отметить, что исследование САУ включает следующие важнейшие этапы:

• моделирование с использованием компьютеров и универсальных (математических) либо специализированных (предметно-ориентированных) пакетов прикладных программ;
• синтез САУ с привлечением современного математического аппарата (методов линейной алгебры, численных методов, теории оптимизации ) и, следовательно, машинных методов расчета;
• проектирование системы управления с использованием аппаратных средств вычислительной техники и их программного обеспечения (операционных систем реального времени, средств автоматизации программирования и проч.).

Первый проект по практической реализации цифровых систем был выдвинут в 1950 году американскими фирмами ТRW и Texaсo. В данном проекте ЭВМ использовалась как средство автоматизации химических процессов. Было установлено, что для успешной реализации цифрового управления требуется

• анализ управляемых процессов;
• хорошие алгоритмы управления.

Эти выводы определили в 60-ые годы интенсивное развитие математических методов управления, ориентированных на использованием ЭВМ. Однако их практическая реализация натолкнулась на ряд препятствий, среди которых низкое быстродействие существовавших средств вычислительной техники, их значительные габариты и стоимость, а также низкая надежность.

Решение проблемы было предложено в середине 70-ых годов с появлением серийных и достаточно дешевых микропроцессоров и микро-ЭВМ, которые могли обеспечить требуемое быстродействие управления, имели малые габариты и высокую надежность. Микропроцессорные устройства начинают постепенно вытеснять традиционные электрические и электронные средства управления (регуляторы) в простейших автоматических системах. Более того с развитием микропроцессорной техники появилась возможность реализации более

сложных алгоритмов для решения нетрадиционных задач управления.

Проектирование, внедрение и эксплуатация современных САУ требует взаимодействия специалистов различных профилей:

• технологов, т.е. специалистов, знающих особенности управляемых процессов и технические требования к проектируемой САУ;
• специалистов по автоматическому управлению, обеспечивающих разработку САУ (алгоритмов управления и контроля);
• специалистов по вычислительной технике для разработки математического обеспечение для проектирования САУ, средств автоматизации программирования, организации вычислений в РВ (ОСРВ) и комплектации технических средств.

Прочтение данной статьи про кибернетические понятия позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое кибернетические понятия, предмет теории управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.