Лекция
Привет, Вы узнаете о том , что такое преобразования фурье, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое преобразования фурье, лапласа , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Преобразование Фурье
Соотношение

называют прямым преобразованием Фурье. Функция угловой частоты  –
– 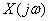 называется Фурье-изображением или частотным спектром функции
называется Фурье-изображением или частотным спектром функции 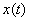 . Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал
. Спектр характеризует соотношение амплитуд и фаз бесконечного множества бесконечно малых синусоидальных компонент, составляющих в сумме непериодический сигнал 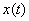 . Операция
преобразования фурье математически записывается следующим образом:
. Операция
преобразования фурье математически записывается следующим образом:

где  - символ прямого преобразования Фурье.
- символ прямого преобразования Фурье.
Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:

На рис. 1 представлено типичное изображение спектра непериодического сигнала.

Рис. 1
Отметим следующие особенности спектра непериодической функции  :
:
Спектр непериодической функции времени непрерывен;
Область допустимых значений аргумента спектра
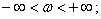
Действительная часть спектра – четная функция частоты, мнимая часть спектра – нечетная функция, что позволяет использовать одну половину спектра

Преобразование Фурье обратимо, то есть, зная Фурье-изображение, можно определить исходную функцию – оригинал. Соотношение обратного преобразования Фурье имеет следующий вид:
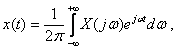
или в сокращенной записи  , где
, где  - символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
- символ обратного преобразования Фурье. Заметим, что временная функция имеет преобразование Фурье тогда и только тогда, когда:
функция однозначна, содержит конечное число максимумов, минимумов и разрывов;
функция абсолютно интегрируема, то есть
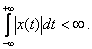
Обратное преобразование Фурье возможно только в том случае, если все полюсы 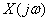 - левые.
- левые.
Рассмотрим примеры определения спектра временных функций.
Пример:
Найдем частотный спектр дельта-функции.
 ,
,
так как при 
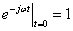 ,
,
а при 
 и
и
 .
.
В итоге,  имеет единичный, равномерный и не зависящий от частоты действительный спектр, а мнимая часть спектра будет равна нулю (см. рис.2).
имеет единичный, равномерный и не зависящий от частоты действительный спектр, а мнимая часть спектра будет равна нулю (см. рис.2).

Рис. 2
Пример:
Найдем частотный спектр единичной ступенчатой функции.
Для этой функции не выполняется требование абсолютной интегрируемости, так как

Поэтому  Фурье-изображения не имеет.
Фурье-изображения не имеет.
Преобразование лапласа
Соотношение

называют прямым преобразованием Лапласа. Комплексная переменная  называется оператором Лапласа, где
называется оператором Лапласа, где 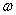 - угловая частота,
- угловая частота, 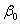 - некоторое положительное постоянное число. Функция комплексной переменной
- некоторое положительное постоянное число. Функция комплексной переменной 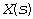 называется изображением сигнала
называется изображением сигнала 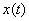 по Лапласу. Операция определения изображения по оригиналу сокращенно записывается -
по Лапласу. Операция определения изображения по оригиналу сокращенно записывается - 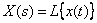 , где
, где 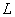 - символ прямого преобразования Лапласа.
- символ прямого преобразования Лапласа.
Преобразование Лапласа обратимо, то есть, зная изображение по Лапласу, можно определить оригинал, используя соотношение обратного преобразования

или 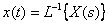 , где
, где 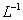 - символ обратного преобразования Лапласа.
- символ обратного преобразования Лапласа.
Отметим, что преобразование Лапласа изображает исходную функцию лишь при 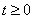 , а поведение исходной функции при
, а поведение исходной функции при 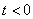 никак не сказывается на изображении. Об этом говорит сайт https://intellect.icu . Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.
никак не сказывается на изображении. Об этом говорит сайт https://intellect.icu . Класс функций, преобразуемых по Лапласу, значительно шире класса функций, преобразуемых по Фурье. Практически любые функции времени в ТАУ имеют преобразование Лапласа.
Получим изображения по Лапласу для импульсных функций.
 ,
,
так как  при
при  ,
,
 , и
, и 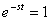 при
при 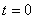 .
.
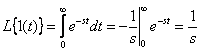 .
.
На практике для выполнения прямого и обратного преобразований Лапласа используются таблицы преобразований, фрагмент которой показан в табл. 1.
Таблица 1.
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Таблицы преобразования Лапласа могут быть использованы для определения Фурье-изображений таких абсолютно интегрируемых функций, которые равны 0 при  . Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу
. Для получения Фурье-изображений в этом случае достаточно положить в изображении по Лапласу  . В общем виде это выглядит как
. В общем виде это выглядит как
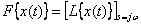 ,
,
если 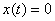 при
при 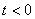 и
и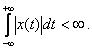
Рассмотрим формулировки основных теорем преобразования Лапласа, которые широко используются в ТАУ.
Теорема линейности. Любое линейное соотношение между функциями времени справедливо и для изображений по Лапласу этих функций;
 ;
;
Теорема о дифференцировании оригинала.
Если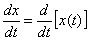 и
и 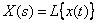 , то
, то  ,
,
где  - начальное значение оригинала.
- начальное значение оригинала.
Для второй производной используют выражение
 .
.
Для производной  -го порядка справедливо следующее соотношение:
-го порядка справедливо следующее соотношение:
 ;
;
Для производной  -го порядка при нулевых начальных условиях справедливо следующее соотношение:
-го порядка при нулевых начальных условиях справедливо следующее соотношение:
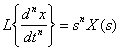 ;
;
то есть дифференцирование  степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на
степени оригинала по времени при нулевых начальных условиях соответствует умножению изображения на  .
.
Теорема об интегрировании оригинала.
 ;
;
Замечание
В области изображений по Лапласу сложные операции дифференцирования и интегрирования сводятся к операциям умножения и деления на 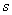 , что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории автоматического управления.
, что позволяет переходить от дифференциальных и интегральных уравнений к алгебраическим. Это является главным достоинством преобразования Лапласа как математического аппарата теории автоматического управления.
Теорема запаздывания. Для любого  справедливо соотношение
справедливо соотношение
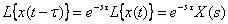 ;
;
Теорема о свертке (умножении изображений).
 ,
,
где
 ;
;
Теорема о предельных значениях. Если 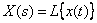 , то
, то
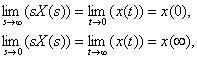
если  существует.
существует.
Для нахождения оригинала функции по ее изображению используют обратное преобразование Лапласа. Функцию изображения необходимо представить в форме Хэвисайта, воспользовавшись необходимой формулой разложения дробно-рациональной функции. Полученную сумму простейших дробей подвергают обратному преобразованию Лапласа. Для этого можно воспользоваться таблицами преобразования Лапласа, которые определяют изображения многих временных функций. Фрагмент таблицы преобразования Лапласа приведен в табл. 1. В тех случаях, когда имеются комплексно-сопряженные полюсы изображения, необходимо преобразовать соответствующие простейшие дроби к виду, удобному для использования таблицы преобразования Лапласа. Существенно облегчает преобразование использование персонального компьютера с пакетами математических программ, содержащих функции прямого и обратного преобразований Лапласа.
Пример
Определим оригинал  по изображению в виде дробно-рациональной функции
по изображению в виде дробно-рациональной функции
 .
.
Используем разложение Хэвисайта для дробно-рациональной функции с одним нулевым полюсом. Тогда
 .
.
Коэффициенты разложения имеют вид
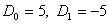 .
.
Изображение в форме Хэвисайта имеет вид
 .
.
Используем теорему о линейности и таблицу преобразований к каждому слагаемому, в результате получаем
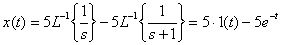 .
.
График функции оригинала имеет вид, показанный на рис. 3.

Рис. 3
Кратко поясним алгоритм решения дифференциальных уравнений операторным методом на примере решения дифференциального уравнения 2 порядка в общем виде
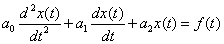 ,
,
где  ,
, 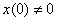 ,
,  .
.
Применим теорему о дифференцировании для нахождения изображений производных
 ,
,  .
.
Пусть 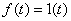 , тогда
, тогда
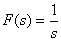 .
.
Получим операторное уравнение, используя теорему линейности
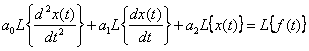 ,
,
 .
.
Решаем уравнение относительно  ,
,
 .
.
Найдем 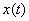 , используя переход к форме Хэвисайта (разложение Хэвисайта)
, используя переход к форме Хэвисайта (разложение Хэвисайта)
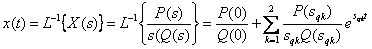 ,
,
где  ,
, 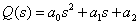 .
.
Особо следует обратить внимание на получение изображения производной ступенчатой единичной функции  , которая определяется следующим образом:
, которая определяется следующим образом:

Если использовать
 ,
,
то получается ошибочное решение, поэтому следует использовать называемые "левые" начальные условия
 .
.
Справедливость этого можно легко проверить подстановкой решения в исходное дифференциальное уравнение.
Контрольные вопросы и задачи
Какие ограничения накладываются на прямое и обратное преобразование Фурье?
Как с помощью таблиц преобразования Лапласа получить частотный спектр реального сигнала – непериодической функции времени?
Если изображение по Лапласу имеет вид дробно-рациональной функции, в какой форме ее удобнее представлять для получения оригинала, в форме Боде или в форме Хэвисайта?
Определите оригинал следующего изображения по Лапласу
 .
.
Ответ:
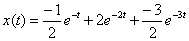 .
.
Определите оригинал следующего изображения по Лапласу
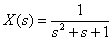 .
.
Ответ:
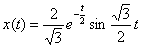 .
.
Найдите 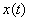 , решив дифференциальное уравнение
, решив дифференциальное уравнение
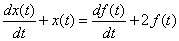 ,
,
где 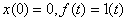 .
.
Ответ:
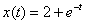 .
.
Найдите  , решив дифференциальное уравнение
, решив дифференциальное уравнение
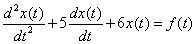 ,
,
где  .
.
Ответ:
 .
.
Прочтение данной статьи про преобразования фурье позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое преобразования фурье, лапласа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про преобразования фурьеОтветы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления