2.1 Линейные модели вход-выход

Привет, Вы узнаете о том , что такое линейные модели вход-выход, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое линейные модели вход-выход , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Математической моделью динамической системы принято называть совокупность математических символов, однозначно определяющих развитие процессов в системе, т.е. ее движение. При этом в зависимости от используемых символов различают аналитические и графоаналитические модели. Аналитические модели строятся с помощью буквенных символов, в то время как графоаналитические допускают применение графических обозначений (см. п.2.1.2).

В зависимости от типа сигналов различаются непрерывные и дискретные модели систем. В зависимости от используемых операторов - линейные и нелинейные, а также временные и частотные модели. К временным относятся модели, в которых аргументом является (непрерывное или дискретное) время. Это дифференциальные и разностные уравнения, записанные в явном виде или в операторной форме. Частотные модели предусматривают использование операторов, аргументом которых является частота соответствующего сигнала, т.е. операторы Лапласа, Фурье и т.д.

В этом разделе рассматриваются непрерывные линейные временные модели динамических систем.

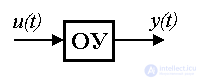
Модель вход-выход (ВВ) - это описание связи входных и выходных сигналов динамической системы. Необходимость в таком описании появляется при рассмотрении поведения отдельных блоков и, в частности, объекта управления (ОУ), так и всей системы управления в целом. Различия в математическом описании блоков и системы управления непринципиальны, но требуют использования разных обозначений (см. п.1.5). Так, входным сигналом САУ является задающее воздействие y*(t), а выходным - переменная y(t). При описании блоков часто используются обозначения x₂(t) и x₁(t), соответственно. В дальнейшем воспользуемся обозначениями, характерными для объекта управления, где входным сигналом является управляющее воздействие u(t) , а выходом регулируемая переменная y(t).

2.1.1. Аналитические модели. Линейная модель вход-выход одноканальной динамической системы ( здесь - объекта управления) может быть представлена обыкновенным дифференциальным уравнением вида:

[ М1 ]  ,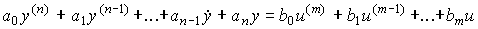

где a_i , b_i -коэффициенты (параметры модели ), a₀ 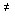 0 , b₀  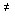0, n - порядок модели, 0 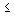m<n . Уравнение [M1] связывает входные сигналы  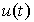и их производные  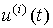с выходными сигналами y(t) и их производными  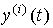на некотором временном интервале, т.е. при  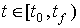. Значения  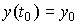,  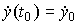,..., 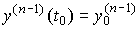называются начальными значениями (условиями), а число r = n - m  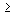1 - относительной степенью модели.

Различают стационарные системы, для которых значения параметров неизменны :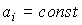 ,  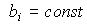и можно положить  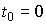, и нестационарные модели, где параметры являются функциями времени, т.е.  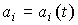,  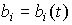. В случае, когда  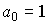, уравнение называется приведенным.

Система, для которой 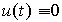 , называется автономной. Описание автономной системы дается однородным дифференциальным уравнением вида

[M1а]                      .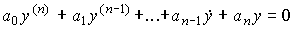

Модель [M1] может быть переписана в операторной форме. Для этого введем в рассмотрение операторы дифференцирования

                    

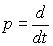
и положим, что

                     .

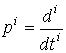С учетом введенных обозначений уравнение [M1] легко преобразуется к операторной форме

[М2]                      ,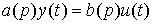

где используются дифференциальные операторы

(2.1)                      ,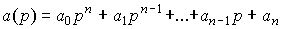

(2.2)                      .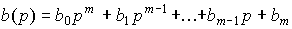

Оператор a(p) является характеристическим полиномом дифференциального уравнения [M1] , а комплексные числа 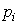 ,  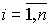, являющиеся корнями характеристического уравнения

(2.3)                      ,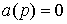

называются полюсами системы [M1]. Дифференциальный оператор b(p) - характеристический полином правой части. Корни уравнения

(2.4)                      ,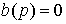

т.е. комплексные числа 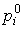 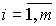 , называются нулями системы [M1].

Из уравнения [М2] найдем явную связь переменных y(t) и u(t) в виде операторного уравнения :

[М3]                      ,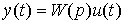

где интегрально - дифференциальный оператор

(2.5)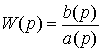                     

называется передаточной функцией системы [M1].

Преимущество использования операторных моделей типа [M2] и [M3] заключается, во-первых, в краткости записи соответствующих уравнений , а во-вторых, в удобстве преобразования сложных (составных) моделей (см. Об этом говорит сайт https://intellect.icu . п 2.4).

Рассмотрим частный случай динамической системы с коэффициентами b₀=b₁=...=b_m-1=0 . При b_m=b 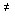 0 система имеет относительную степень r=n-1,  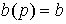и нули отсутствуют. Уравнение [M1] принимает вид

(2.6)                      ,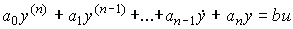

уравнение [M2] -

(2.7)                      ,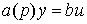

а уравнение [M3] -

(2.8)                      .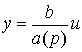

Пример 2.1. Пусть 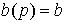 и 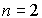 . Дифференциальное уравнение системы имеет вид

                    

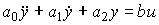
с начальными условиями 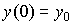 ;  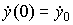. Здесь  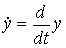- скорость выходной переменной. Операторная форма модели -

                     ,

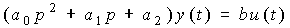и

                     .

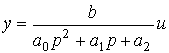Характеристическое уравнение системы

                    

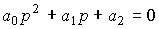
имеет два (вещественных или комплексных) корня

                     .

 

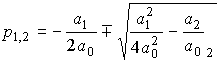2.1.2. Структурные схемы. Наиболее распространенной графоаналитической формой модели динамической системы является структурная схема - разновидность направленного графа. Элементами такой схемы являются (рис. 2.1)

 

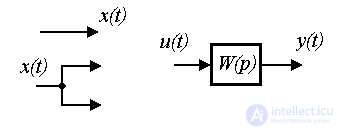
Рис. 2.1. Элементы структурной схемы

• буквенные обозначения сигналов (x(t), u(t), y(t) и т. д.) и т.д.;
• буквенные обозначения операторов (например, W(p));
• графические обозначения - стрелки, указывающие направление действия сигналов, узлы (разветвления сигналов), блоки c указанием входных и выходных сигналов, а также операторов, описывающих связи между сигналами.

К простейшим блокам, использующихся в структурных схемах, относятся (рис. 2.2):

• блок сравнения;
• сумматор;
• пропорциональный блок;
• интегратор

(см. также п. 2.3).

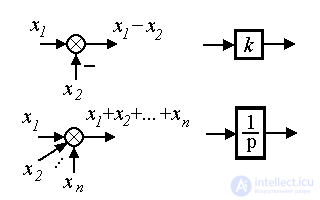
Рис.2.2. Простейшие блоки

Пример 2.2. Модели вход-выход нагревательной печи, RC- цепочки и разгона электродвигателя (см. пример 1 .1) описываются дифференциальным уравнением первого порядка

(2.9)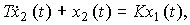                     

где T, K - постоянные коэффициенты (параметры). Операторная форма модели имеет вид

(2.10)                      .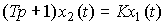

Здесь 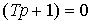 - характеристическое уравнение, которое имеет один корень (полюс системы) p₁=-1/T . Из уравнения (2.10) находим операторную связь входа и выхода

                   

 .

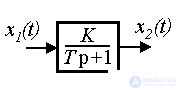
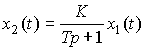Следовательно, передаточной функцией блока является оператор

                     .

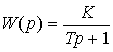Заметим, что уравнение (2.9) можно привести к виду

(2.11)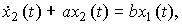                     

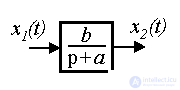
где a=1/T, b=K/T . Тогда операторная форма (2.10) принимает вид

(2.12)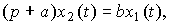                     

а форма (2.12) -

                     .

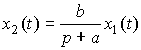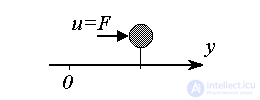
Пример 2.3. Рассмотрим движение материальной точки массы m под действием силы (входного воздействия) u=F(t) . Данная динамическая система описывается уравнением второго порядка (2-ым законом Ньютона)

(2.13)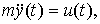                     

с начальными условиями y₀=y₀(0), 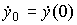 , где y(t) - линейное перемещение. Операторная форма модели принимает вид

(2.14)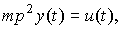                     

а характеристическое уравнение системы

(2.15)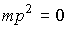                     

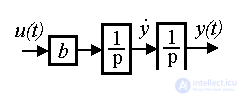
имеет два корня (полюса системы) p_1,2=0 . Из уравнения (2.14) находим операторную связь входа и выхода

(2.16)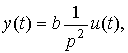                     

где b=1/m. Следовательно, передаточной функцией блока является оператор

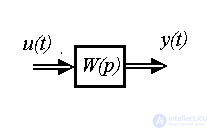
(2.17)                      .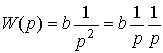

В структурных схемах многомерных и многоканальных систем векторные сигналы 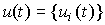 ,  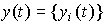и 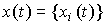 иногда выделяют двойными стрелками.

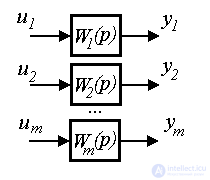
2.1.3. Многоканальные модели. Сначала рассмотрим многоканальную систему с независимыми (автономными) каналами. Система описывается m операторными уравнениями

[M2m]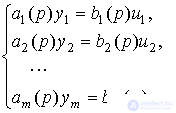                     

каждое из которых характеризует поведение одного из ее каналов.

Введем в рассмотрение векторы выходных переменных y и управления u:

                     ,  ,

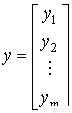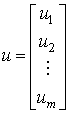соответственно, и запишем систему уравнений в векторно-матричной форме:

                     

или,

[М2m]                     A(p)y=B(p)u

Если матрица A(p) - обратима, т.е. существует обратная матрица

                     ,

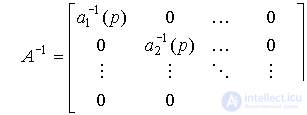то из уравнения [М2m] найдем

[М3m]                     y=W(p)u,

где W(p)= {W_ij } - передаточная матрица системы (матричный интегро-дифференциальный оператор), вычисляемая как

                    W(p)=A^-1(p)B(p)=  .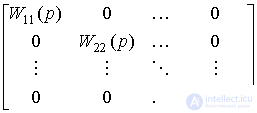

Легко видеть, что в рассматриваемом случае передаточная матрица является диагональной, т.е.

                    W(p)=diag{W_ii(p)}={b_i(p)/a_i(p)}.

Теперь рассмотрим многосвязную систему, т.е. многоканальную систему со связанными каналами, описываемую системой операторных уравнений

                    

a₁₁(p)y₁+a₁₂(p)y₂+...+a_1m(p)y_m=b₁₁(p)u₁+b₁₂(p)u₂+...+b_1m(p)u_m

                    

a₂₁(p)y₁+a₂₂(p)y₂+...+a_2m(p)y_m=b₂₁(p)u₁+b₂₂(p)u₂ +...+b_2m(p)u_m

[M2m]                    . . .

                    

a_m1(p)y₁+a_m2(p)y₂+...+a_mm(p)y_m=b_m1(p)u₁+b_m2(p)u₂ +...+b_mm(p)u_m

Система приводится к векторно-матричной форме [M2m ], где

                     ; 

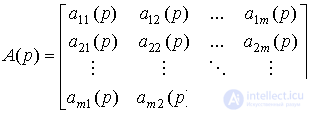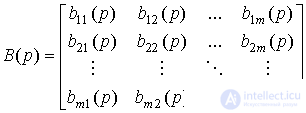
и форме [M3m] , где передаточная матрица W(p) определяется выражением

                    W(p)=A^-1(p)B(p)=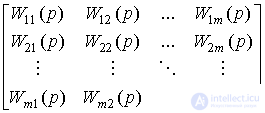

Модель [M3m] можно также записать в скалярном виде:

                    y₁=W₁₁(p)u₁+ W₁₂(p)u₂ +...+W_1m(p)u_m

                    y₂=W₂₁(p)u₁+ W₂₂(p)u₂ +...+W_2m(p)u_m

                    . . .

                    y_m=W_m1(p)u₁+ W_m2(p)u₂ +...+W_mm(p)u_m

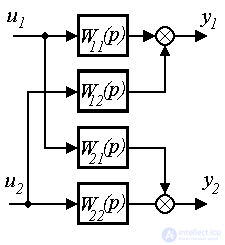
Отметим, что диагональные операторы W_ii(p) относятся к основным каналам , а остальные передаточные функции W_ij(p) характеризуют перекрестные связи многоканальной системы.

Для двухканальной многосвязной системы ( m=2) получаем:

                    y₁=W₁₁(p)u₁+ W₁₂(p)u₂,

                    y₂=W₂₁(p)u₁+ W₂₂(p)u₂,

где W₁₁(p), W₂₂(p) - передаточные функции основных каналов системы, а W₁₂(p), W₂₁(p) - передаточные функции перекрестных связей.

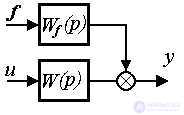
2.1.4. Возмущенная модель системы. Возмущающее воздействие f(t), характеризующее влияние на объект управления внешней среды (см. п. 1.2), рассматривается как дополнительный входной сигнал. 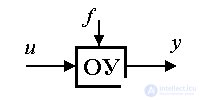Тогда линейная модель одноканальной динамической системы принимает вид

[М1f]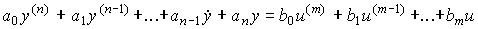  

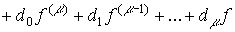
где d_i -коэффициенты, определяющие влияние на процессы в системе возмущения f(t) и его производных f ⁽ⁱ⁾(t), d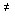₀  0 , 0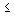 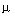 <n. После подстановки операторов дифференцирования pⁱ и соответствующих преобразований получаем операторную форму модели [M1f]:

[М2f]                      ,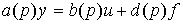

где используется дифференциальный оператор

                     .

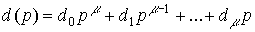Явная операторная форма приобретает вид

[М3f]                      ,

где

                     .

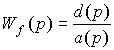передаточная функция по возмущающему воздействию f(t).

Прочтение данной статьи про линейные модели вход-выход позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое линейные модели вход-выход и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления