Временные и частотные характеристики колебательного звена

Привет, Вы узнаете о том , что такое временные, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое временные, частотные характеристики колебательного звена , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Колебательное звено является элементарным динамическим звеном второго порядка, обладает тремя варьируемыми параметрами. Поэтому его характеристикам уделим более пристальное внимание. Тем более, что колебательным звеном описываются достаточно сложные элементы электромеханических систем и электроприводов, на пример, такой распространенный элемент как электродвигатель постоянного тока.

Передаточная функция колебательного звена –

(1)

где 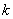 – коэффициент усиления,  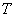– постоянная времени,  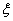– коэффициент затухания.

Отличительной особенностью колебательного звена является то, что оно меняет не только свои свойства, но и название в зависимости от величины коэффициента затухания:

• если 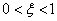 – звено называют колебательным, так как его временные характеристики носят колебательный характер;

• если 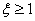 – звено называют инерционным (апериодическим) звеном второго порядка, так как его временные характеристики носят монотонный характер, то есть колебания отсутствуют;

• если 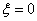 – звено называют консервативным, так как его временные характеристики имеют вид незатухающих колебаний, говорят, звено консервирует колебания.

Получим временные характеристики колебательного звена. Для этого преобразуем его передаточную функцию (1), вводя обозначения –

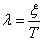 – показатель затухания,

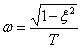 – угловая частота колебаний,

(2)

Из таблиц преобразования Лапласа имеем –

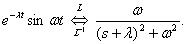
Теперь мы можем определить импульсную характеристику колебательного звена –

(3)

Примерный вид импульсной характеристики показан на рис. 1.

Рис. 1

Определим переходную характеристику колебательного звена –

(4)

Примерный вид переходной характеристики показан на рис. 2.

Рис. 2

По рис. 1 и 2 можно легко судить, как влияют параметры колебательного звена временные характеристики.

Подвергнем более подробному анализу временные характеристики колебательного звена для случая 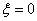, то есть, определим временные характеристики консервативного звена.

Передаточная функция консервативного звена имеет вид –

,

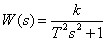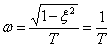 – угловая частота колебаний,

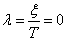 – показатель затухания.

тогда выражения временных характеристик (3) и (4) примут следующий вид –

(5)

(6)

Примерный вид характеристик консервативного звена показан на рис. Об этом говорит сайт https://intellect.icu . 3 и 4.

Рис. 3

Рис. 4

Определим частотную характеристику колебательного звена.

(6)

ВЧХ –

(7)

МЧХ –

(8)

АЧХ –

(9)

ФЧХ –

(10)

Построим ВЧХ и МЧХ на одном графике, примерный вид характеристик показан на рис. 5.

Рис. 5

Примерный вид АФЧХ показан на рис. 6.

Рис. 6

Примерный вид АЧХ и ФЧХ показан на рис. 7 и 8, функция АЧХ имеет экстремум (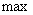) при

.

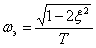Рис. 7

Рис. 8

Рассмотрим частотные характеристики консервативного звена ().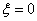

.

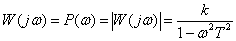При 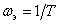 характеристики (см. рис. 9) имеют разрыв

.

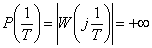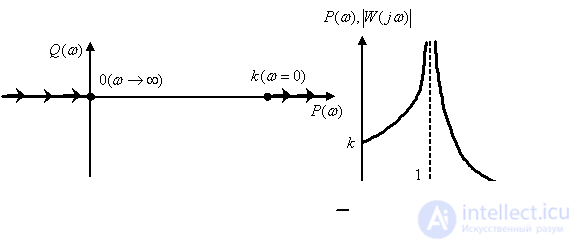
Рис. 9

Определим ФЧХ консервативного звена –

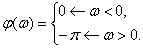
Примерный вид ФЧХ показан на рис. 10.

Рис. 10

Определим логарифмические характеристики колебательного звена.

(11)

Определим асимптотическую ЛАЧХ колебательного звена

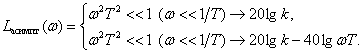
Наклон асимптоты –

.

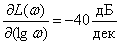Максимальное отклонение асимптотической ЛАЧХ от точной –

.

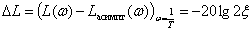Примерный вид ЛАЧХ и ЛФЧХ показан на рис. 11.

Рис. 11

Для получения временных характеристик инерционного звена второго порядка (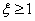) пригодны и выражения (3) и (4), полученные выше для колебательного звена. Но они могут быть получены и иначе.

Если 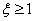, можно преобразовать передаточную функцию звена –

(12)

где

.

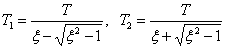Звено с передаточной функцией в виде (12), можно представить в идее двух апериодических звеньев, включенных последовательно, как это показано на рис. 12.

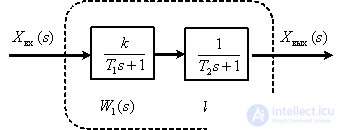
Рис. 12

Импульсные характеристики этих звеньев имеют вид –

.

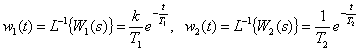Тогда импульсная характеристика инерционного звена второго порядка может быть получена с использованием теоремы преобразования Лапласа об умножении изображений –

(13)

Переходную характеристику получим, интегрируя (13) –

(14)

Примерный вид временных характеристик инерционного (апериодического) звена второго порядка показан на рис. 13.

Рис. 13

Получим асимптотическую ЛАЧХ для инерционного звена второго порядка, представляя его в виде двух последовательно включенных апериодических звеньев, (см. рис. 12).

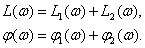
На рис. 14 и 15 показаны ЛАЧХ инерционного звена второго порядка.

Рис. 14

Рис. 15

 

Контрольные вопросы и задачи

1. Как изменяется и в зависимости от чего название колебательного звена?

2. Передаточная функция звена –

.

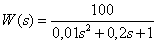Определите частоту колебаний временных характеристик этого звена.

Ответ:

Частота колебаний .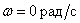

1. Передаточная функция звена –

.

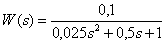Определите показатель затухания временных характеристик этого звена.

Ответ:

Показатель затухания .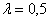

1. Передаточная функция звена –

.

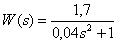Определите частоту колебаний временных характеристик этого звена.

Ответ:

Частота колебаний .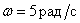

1. Сколько квадрантов проходит АФЧХ колебательного звена?

Ответ:

Два квадранта.

1. На какой частоте имеет разрыв АЧХ консервативного звена, если его передаточная функция имеет вид –

.

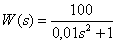Ответ:

Частота разрыва АЧХ .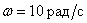

1. На какой угол сдвигает гармонический сигнал с частотой 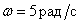 динамическое звено с передаточной функцией –

,

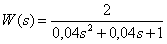и чему равно значение АЧХ при этой частоте?

Ответ:

Угол сдвига фазы составляет 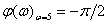, значение АЧХ – .

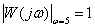Прочтение данной статьи про временные позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое временные, частотные характеристики колебательного звена и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про временные

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.