3.1 Понятие пространства состояний и модели состояние-выход

Привет, Вы узнаете о том , что такое понятие пространства состояний, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое понятие пространства состояний, модели состояние-выход , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

 

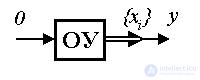
3.1.1. Переменные состояния. Рассмотрим автономную динамическую систему [M1a] с выходом 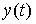 , где 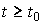 . Отметим, что для автономной системы решение  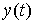содержит только свободную составляющую:  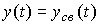. Введем в рассмотрение переменные

(3.1) 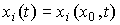                     , i=1,2,...n

с начальными значениями 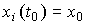 , определенные при  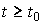и дадим следующее определение [7].

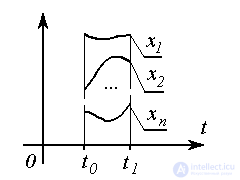
Переменными состояния называются линейно-независимые переменные x_i(t ) такие, что их значения 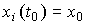 в момент времени t₀ однозначно определяют состояние системы в любой момент времени  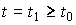, т.е. позволяют найти значения выходной переменной y(t ) в произвольные моменты времени t по формуле

(3.2)                      .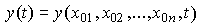

Процедура нахождения значений некоторой функции 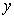 (t) для моментов времени  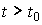называется прогнозированием (см. п. 1.1.1). Возможность прогназирования является естественным требованием качественного управления, что определяет важность введенного понятия для рассматриваемых далее неавтономных (управляемых) систем. При этом отличительной особенностью переменных состояния является то, что для предсказания поведения системы в любой момент времени t > t₀ (и управления неавтономной системой) достаточно информации о переменных состояния в момент t₀ и не требуется знания предистории процесса, т.е. функций x_i(t ) при t < t_0. Последнее служит основанием для построения процедур (алгоритмов) прогнозирования и управления динамическими системами по текущим значениям переменных состояния (см. п. 4.3).

В качестве переменных состояния автономной системы могут быть выбраны, в частности, фазовые переменные системы, т.е. выходная переменная y(t ) и n-1ее производных 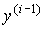 (t), 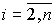 . Введем в рассмотрение переменные

(3.3)                      ,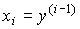 

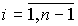
с начальными значениями

(3.4)                      .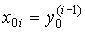

Выход стационарной автономной системы [М1а], т.е. свободная составляющая процесса при 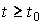 =0, для случая неравных корней характеристического уравнения определяется формулой (см. п. 2.2)

(3.5)                      ,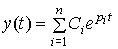

где коэффициенты C_i зависят от начальных значений выходной переменной и ее производных, или с учетом введенных обозначений:

(3.6)                      .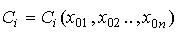

Таким образом, поведение рассматриваемой системы при 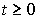 однозначно определяется начальными значениями переменных x_i и, следовательно, по определению эти переменные являются переменными состояния. Общее число переменных состояния равно  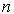, т.е. порядку дифференциального уравнения [М1а]. Линейные комбинации переменных x_i , дополняемые к уже выбранному набору, не являются переменными состояния, так как приводят к линейной зависимости переменных.

Учитывая введенные обозначения, преобразуем уравнение [М1а] к нормальной форме Коши. Дифференцируя по времени уравнение (3.5) и подставляя в полученные выражения (3.3) и [М1а], находим так называемые уравнения состояния автономной системы

(3.7)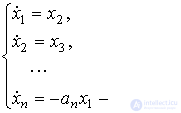                     

Выходная переменная y(t ) связана с переменными состояния тривиальным выражением (уравнением выхода )

(3.8)                      .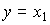

Уравнения состояния (3.7) и выхода (3.8) представляют собой простейший пример модели состояние-выход (СВ).

Замечание 3.1. Выбор переменных состояния динамической системы неоднозначен. В качестве таких переменных могут быть взяты не только фазовые переменные 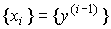 ,  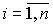, но и физические переменные системы такие, как перемещение, скорость, ток, напряжение и т.д. (см. 4.1), а также любые другие n линейно независимых переменных, полученных, например, как линейные комбинации фазовых и/или физических координат.

Естественно, что выбор переменных состояния определяет структуру и параметры модели состояние-выход. Кроме указанного выше способа построения такой модели в стандартной форме (3.7), (3.8), модель СВ может быть получена как совокупность моделей реальных физических процессов, часто соответствующих элементарным звеньям 1-ого порядка (см п. 2.3).

3.1.2. Модели состояние-выход и переходные процессы. В наиболее общем случае уравнения состояния автономной системы представлены в нормальной форме Коши, т.е. в виде системы 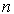 однородных дифференциальных уравнений

[М4а]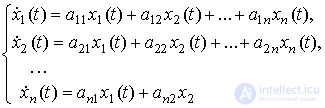                     

где 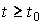 ,  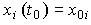,  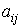- постоянные или зависящие от времени коэффициенты (параметры), а уравнение выхода, связывающее выходную переменную системы y(t ) с переменными x_i(t ) имеет вид

[М5]                      ,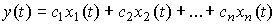

где 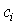 - коэффициенты (параметры). Нетрудно показать (см. ниже), что переменные x_i(t ) действительно являются переменными состояния и, поэтому уравнения [М4а] и [М5] представляют наиболее общую модель состояние- выход линейной автономной динамической системы.

Вектор x=x(t) размерности n , элементами которого являются переменные состояния x_i= x_i(t), т.е.

(3.9)                      = ,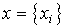

называется вектором состояния. Об этом говорит сайт https://intellect.icu . Вектор x является элементом n - мерного линейного (векторного) пространства 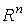 , которое называется пространством состояний :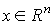 

Уравнения [М4а], [М5] можно записать в векторно-матричной форме:

[М6а]                      ,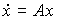

[М7]                      ,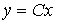

где 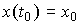 ,  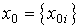-вектор начальных состояний (начальных условий),

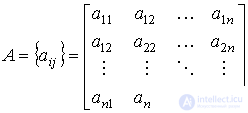                     - матрица системы размера  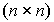,  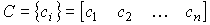- матрица выхода размера  .

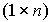В частном случае, когда уравнения модели ВС представлены в виде (3.7) (3.8), получаем

                     ,  .

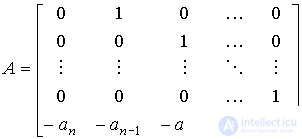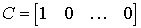Решением системы дифференциальных уравнений [M4а] с начальными условиями 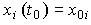 называется набор функций

(3.10)                      ,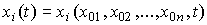

которые при t = t₀ удовлетворяют начальным условиям, а для любых 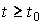 - уравнениям [M4а]. Соответственно, решением уравнения [М6а] будет вектор-функция

(3.11)                      .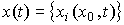

Решение может быть представлено как

(3.12)                      ,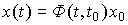

где 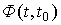 - фундаментальная (переходная) матрица системы [М6а]. Подставляя (3.12) в уравнение выхода [M7] , получим выражение для расчета выходной переменной

(3.13)                      .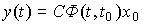

Для стационарных систем переходная матрица находится как

(3.14)                      .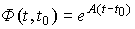

Полагая 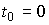 , найдем:

(3.15)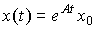                     

и

(3.16)                      .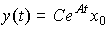

Замечание 3.2. Анализ уравнений (3.14) - (3.16) показывает следующее.

1. Выходная переменная 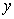 (t ) в любой момент времени  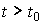однозначно определяется n начальными значениями  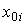и, следовательно, по определению переменные  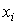действительно являются переменными состояния.

2. Предистория системы (ее движение при 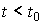 ) не влияет на поведение системы при  .

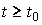Если для некоторых начальных условий и 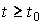 имеет место тождество

(3.17)                      ,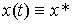

где x*=const , то значение x=x* называется равновесным состоянием, или положением равновесия , автономной системы [M6a] .Очевидно, что в равновесном состоянии выполняется

(3.18)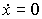                     

и, следовательно,

(3.19)                      .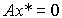

При условии, что det A 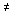 0, получаем, что единственным положением равновесия системы [M6a] является начало координат пространства состояний Rⁿ , т.е.

                    x*=0,

а при det A =0 - существуют нетривиальные множества равновесных состояний (прямые, плоскости, т.е. подпространства, удовлетворяющие уравнению ( 3.19)).

После подстановки x* =0 в уравнение выхода [ M7 ], находим равновесное значение выходной переменной (см. п. 2.2.2)

                    y*=0.

Формулы ( 3.14) - (3.16) определяют переходные процессы системы - 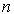 функций времени  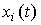. Графически они могут быть представлены в виде:

• временных диаграмм (см. п. 2.2);
• интегральных кривых .

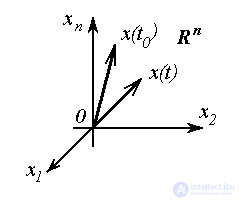
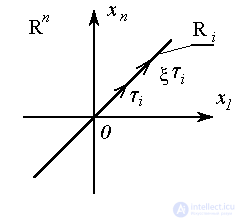
Интегральной кривой (фазовой траекторией) называется линия, описываемая вектором состояния 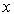 в пространстве состояний  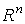при изменении переменной  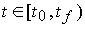,  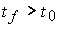, т.е. годограф вектор-функции x(x₀, t ) по параметру  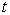. Фазовый портрет - множество фазовых траекторий, соответствующих различным значениям начальных условий  .

 

 

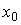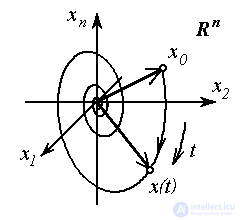
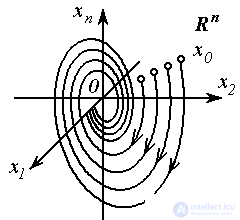
Рис. 3.1. Интегральная кривая в Rⁿ и фазовый портрет

Введенные выше понятия обобщаются на класс многоканальных (многосвязных, см. п. 2.1.3 ) систем, которые характеризуются несколькими выходными переменными y_j , 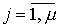 . Общая модель многоканальной системы включает уравнения состояния [М4а] и  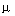уравнений выхода

[М5m]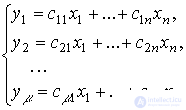                     

где 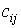 - коэффициенты (параметры).

Определим 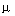 -мерный вектор выходов

(3.20)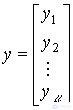                     

как вектор пространство выходных переменных R 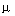 и запишем уравнение [M5m] в компактной векторно-матричной форме [M7], т.е.

[М7m]                      ,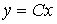

где 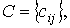 - матрица выходов размера  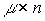. Таким образом модель состояние-выход многоканальной системы представлена уравнениями [M4], [M5m] или векторно-матричными уравнениями [M6а] и [M7m].

3.1.3. Свойства моделей состояние-выход . Проанализируем решения уравнения состояния [M6a], [M7] и связанные с ними переходные процессы автономной динамической системы (3.12) - (3.16).

Прежде всего определим

• собственные значения (собственные числа) матрицы состояния A как n чисел  ;
• характеристическое уравнение

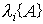(3.21)                       ;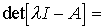

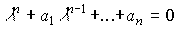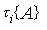• собственные векторы матрицы как  ,

а также (для случая вещественных собственных чисел 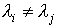 ) собственные подпространства системы как множества ( прямые, плоскости и т.д. )

(3.22)                                          ,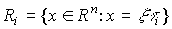

где 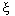 - вещественные числа. Напомним, что в рассматриваемом случае собственные векторы удовлетворяют уравнениям

(3.23)                      .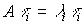

Матричная функция

(3.24)                      =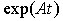

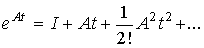
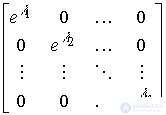
называется матричной экспонентой. Матричная экспонента диагональной матрицы

                     ;

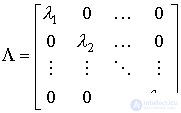рассчитывается по простой формуле

(3.25)                      .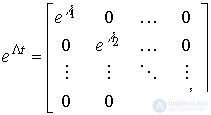

В более общем случае (при условии 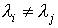 ) из выражения (3.23) получаем:

                      

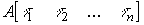
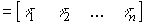
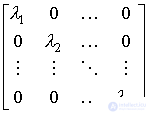
и, следовательно, матрица A связана с диагональной матрицей 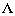 формулой

(3.26)                      ,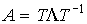

где

 .

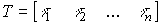Тогда матричная экспонента находится как

(3.27)                      .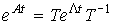

Теперь, учитывая уравнение (3.27) перепишем формулу для расчета вектора состояния (3.15) как

(3.28)                      .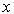

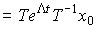
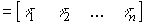
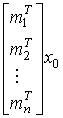Учитывая, что 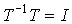 , запишем

                    

и, следовательно,

                     .

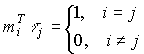Тогда уравнение (3.28) принимает вид

(3.29)                      .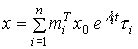

Введем обозначения

(3.3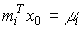0)                      (x₀)

и запишем формулу (3.29) в виде разложения по собственным векторам

(3.31)                       ,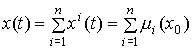

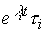где векторы 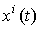 принадлежат собственным подпространствам системы  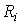и называются собственными составляющими решения x(t), или модами вектора состояния системы.

Замечание 3.3. Если начальное значение вектора состояния принадлежит собственному подпространству 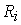 , т.е.  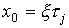, то

(3.32)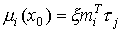                      

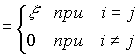
и, следовательно,

(3.33)                       ,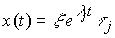

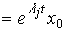т.е. траектория системы целиком лежит в собственном подпространстве R_i.

Такого рода подпространства пространства состояний Rⁿ относятся к классу инвариантных множеств динамической системы.

Проанализируем поведение выходной переменной y(t) . Подставляя уравнение ( 3.31 ) в [M7] находим:

(3.34)                       ,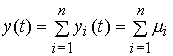

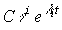где y_i(t) - моды выходной переменной.

Сравнивая последнее уравнение с выражением (2.20), получим, что неопределенные коэффициенты C_i могут быть рассчитаны как

(3.35)                      .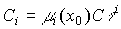

Более того,

(3.36)                      ,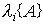

т.е. полюсы системы p_i совпадают с собственными числами матрицы 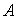 . Отсюда следует, что совпадают и характеристические уравнения (2.3) и (3.21), или

(3.37)                      .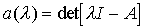

Таким образом получены следующие свойства моделей состояние-выход.

Свойство 3.1.

                     .

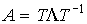Свойство 3.2.

                     .

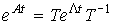Свойство 3.3.

                     .

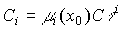Свойство 3.4.

                     .

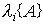Свойство 3.5.

                     .

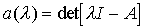Прочтение данной статьи про понятие пространства состояний позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое понятие пространства состояний, модели состояние-выход и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления