4.1 Модели электромеханических объектов

Привет, Вы узнаете о том , что такое модели электромеханических объектов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое модели электромеханических объектов , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Типовой электромеханический объект (ЭМО) содержит многоканальный исполнительный электропривод (ЭП , см. п. 1.2.1) и управляемый кинематический механизм (КМ). В качестве кинематических механизмов электромеханических систем выступают многокоординатные механизмы станков, роботов, поточных линий, рулевые устройства летательных аппаратов и транспортных средств, подвижные элементы автоматического оборудования и приборов. Электропривод служит для преобразования маломощных электрических сигналов, поступающих от устройства управления (управляющей ЭВМ), в механические воздействия (силы и моменты) достаточной мощности, прикладываемые к нагрузке, т.е. к кинематическому механизму. Каждый канал привода (см. рис. 4.1) обеспечивает поступательное или вращательное движение соответствующего звена КМ и содержит усилитель мощности входного сигнала (У), электродвигатель (ЭД) и редуктор.

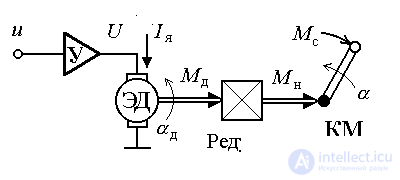
Рис. 4.1. Электромеханических объект

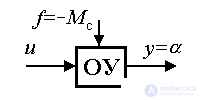
Рассмотрим математическую модель одноканального электромеханического объекта (рис. 4.1), в состав которого входит одно вращательное звено механизма и одноканальный электропривод. Выходом объекта служит угловое перемещение КМ y= 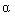 , а его входом - управляющий сигнал u ; момент сопротивления М _c , приложенный к валу нагрузки, выступает в качестве возмущающего воздействия : f = - M_c.

4.1.1. Точная модель ЭМО . Для построения математической модели объекта используются известные из физики уравнения, описывающие его функциональные элементы.

Кинематический механизм описывается уравнениями, полученными на основании второго закона Ньютона:

(4.1)                      ,

(4.2)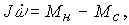                     

где 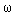 - скорость вращения вала КМ,  - вращающий момент приложенный к валу, 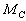 - приведенный момент сопротивления, J - приведенный момент инерции.

На структурной схеме (рис. 4.2) механизм представлен двумя интегрирующими звеньями и пропорциональным звеном с коэффициентом 1/J.

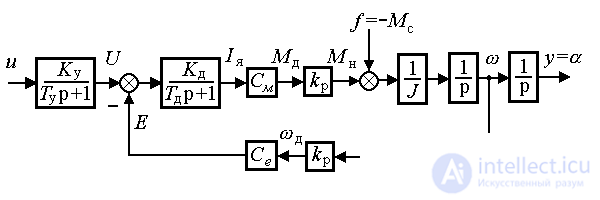
Рис. 4.2. Структурная схема ЭМО

Редуктор обеспечивает преобразование (обычно усиление) момента двигателя M _д в момент нагрузки M _н по формуле

(4.3)                      ,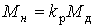

где k _р - коэффициент передачи редуктора ( k _р =1/i _р , где i _р - передаточное отношение редуктора). При этом скорости вращения ЭД 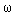 _д и вала КМ 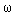связаны соотношением

(4.4) 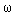                     = k _р  .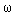

На структурной схеме редуктор представлен пропорциональными звеньями.

Модель электродвигателя задается моментной характеристикой

(4.5)                      ,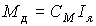

где I _я - ток якоря, C _М - механическая постоянная, и уравнением якорной цепи

(4.6)                      ,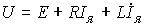

где U - напряжение, приложенное к якорю ЭД (выход усилителя мощности), E - противо - ЭДС , L и R - индуктивность и сопротивление якорной цепи, соответственно. Об этом говорит сайт https://intellect.icu . Последнее выражение удобно привести к виду

(4.7)                      ,

где T _д = L /R - постоянная времени, а K _д =1/L - коэффициент передачи якорной цепи. Противо-ЭДС определяется известной формулой

(4.8)                     E = C_e 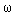 д = C_e k _р  ,

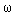где C _е - электрическая постоянная.

На структурной схеме электродвигатель представляется апериодическим звеном (4.7) и двумя пропорциональными звеньями с коэффициентами передачи С_е и С_м .

Усилитель мощности является апериодическим звеном, описываемым уравнением

(4.9)                      ,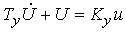

где T _у и К_у - постоянная времени и коэффициент усиления, соответственно.

4.1.2. Построение моделей ВВ и ВСВ. С использованием методов преобразования структурных схем (см. п. 2.4) по уравнениям (4.1)-(4.9) может быть найдена связь выхода объекта y = 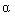 и его входов u и f = - M _с , т.е. модель вход-выход ЭМО вида [ М2 ]:

(4.10)                     (p⁴ +a₁ p³ +a₂ p² +a₃ p)y(t)=b₀ u +(d₀ p² +d₁ p +d ₂)f,

где a₁, a₂, a₃, b₀, d₀, d₁, d ₂ - постоянные коэффициенты. Модель (4.10) приводится к виду [М3]:

(4.11)                      ,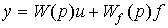

где W(p) и W_f (p) - передаточные функции по управляющему воздействию и возмущению, определяемые выражениями

 ,  .

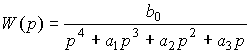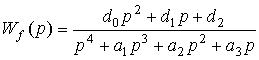Модель вход-состояние-выход (ВСВ) строится либо на основе модели (4.10), либо непосредственно с использованием полученных ранее уравнений функциональных элементов объекта и схемы рис.4.2. В последнем случае уравнения (4.1)-(4.9) преобразуются к системе 4-х дифференциальных уравнений (форма Коши) вида:

(4.12)                      ,

(4.13)                      ,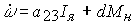

(4.14)                      ,

(4.15)                      ,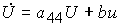

где a_ij, b, d - постоянные коэффициенты. Вектор состояния определяется как

(4.16)                      ,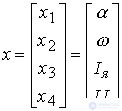

а возмущающее воздействие - f = - M_c . После этого уравнения состояния (4.12) - (4.15) записываются в векторно-матричной форме

[М6f]                      ,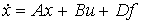

а уравнение выхода получается из выражения y=x₁ и записывается в векторно-матричной форме

[М7]                      .

Переходные процессы системы при единичном входном воздействии u=1(t ) (переменные состояния и само входное воздействие) представлены на рис. 4.3.

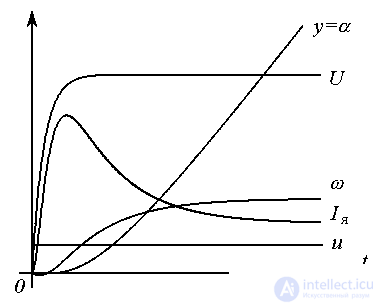
Рис. 4.3. Переходные процессы электромеханического объекта

4.2.3. Приближенная модель ЭМО . Для случая, когда инерционность электрических процессов в электродвигателе и усилителе мощности не значительна по сравнению с инерционностью механических процессов , соотвествующими постоянными времени T _у и T _д можно пренебречь. Полагая T _у = T _д = 0 перепишем уравнения (4.7), (4.9) в виде

(4.17)                     I _я = K _д (U-E),

(4.18)                     U = K _у u.

Тогда уравнение (4.2) после подстановки выражений (4.3), (4.5), (4.6), (4.17) и (4.18) принимает вид

(4.19)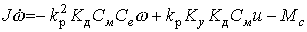                     

или

(4.20)                     

где Т, K, K_f - постоянные коэффициенты.

Таким образом, приближенная модель ЭМО описывается уравнениями (4.1), (4.20) и представлена интегрирующим, апериодическим и двумя пропорциональными звеньями (рис.4.4). Модель вход-выход описывается операторным уравнением вида

 

Рис. 4.4. Схема приближенной модели ЭМО

(4.21)                     (p² +a p)y(t)=b u +df,

где a=1/T, b=K/T, d =K_f/T - постоянные коэффициенты, и приводится к виду (4.11) , где

                     ,  .

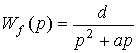Для получения модели ВСВ определяется вектор состояния

                     ,

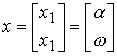и уравнения (4.1), (4.20) переписываются в виде

(4.22)                      ,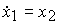

(4.23)                      ,

Далее система уравнений ( 4.22 ), (4.23), а также выражение y = x₁ переписываются в матричном виде [М6f], [M7].

Переходные процессы для упрощенной модели ЭМО при единичном входном воздействии u=1(t) представлены на рис. 4.5.

 

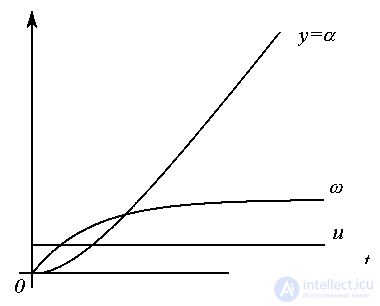
Рис. 4.5. Переходные процессы приближенной модели ЭМО

Прочтение данной статьи про модели электромеханических объектов позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое модели электромеханических объектов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про модели электромеханических объектов