1.4 Локальные задачи управления и контроля

Привет, Вы узнаете о том , что такое локальные задачи управления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое локальные задачи управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

локальные задачи управления устанавливают желаемый характер изменения переменных объекта управления. В зависимости от структуры объекта различают задачи одноканального и мноканального управления (рис. 1.20).

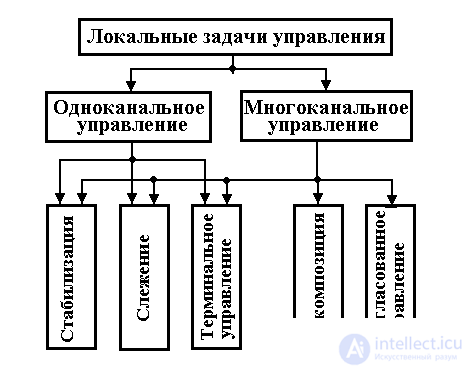
Рис. 1.20

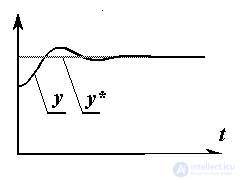
1.4.1. Одноканальное управление и понятие качества системы. В одноканальных задачах управления, к которым относятся задачи стабилизации, слежения и терминального управления, выходная переменная y(t ) является скалярной функцией времени.

Задача стабилизации, или регулирования, формулируется как задача поддержание выходной переменной на заданном уровне y*

                    y = y* = const.

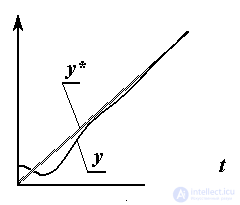
Задача слежения - это задача соблюдения заданного закона y*(t ) изменения переменной y , т.е.

                    y = y*(t).

При этом различают:

• задачи слежения за внешним объектом (объектом слежения - ОС), когда функция y* (t) является выходом ОС и заранее неизвестна;
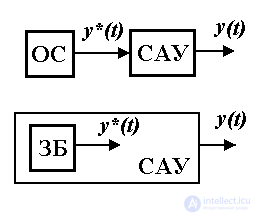• задачи программного управления, в которых программа движения y*(t ) генерируется специальным задающим блоком, входящим в состав устройства управления САУ.

Система автоматического управления, решающая задачи слежения называется следящей системой. Сигнал y*(t ), определяющий требуемый закон движения, системы называется задающим воздействием. Сигнал

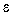                     (t) = y*(t)-y(t),

 

характеризующий текущее значение отклонения выходной переменной от задающего воздействия называется рассогласованием, ошибкой, или отклонением. При этом значение 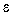 ₀ = 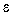 (0) = y*(0) - y (0) - начальное рассогласование системы. Тогда задачи стабилизации и слежения иначе могут быть сформулированы как задачи поддержания нулевого значения рассогласования, т.е.  . 

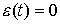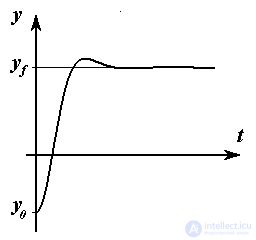
Задача терминального управления заключается в "перемещении" объекта управления в заданную (обычно удаленную) конечную (терминальную) точку y_f :

                    y  y_f.

Основная особенность терминальной задачи, отличающая ее от задачи стабилизации, заключается в том, что величина начального отклонения  ₀ = y_f - y₀ достаточно велика. Об этом говорит сайт https://intellect.icu . Это обуславливает необходимость выбора особой стратегии управления (минимизации быстродействия или энергетических затрат, необходимости соблюдения ограничений на управляющие сигналы и переменные состояния и т.д.).

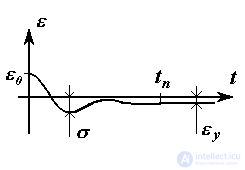
Полное устранение рассогласования 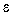 в реальных системах не достигается, причиной чему служат ненулевые начальные значения  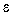₀ , быстрые изменения задающих воздействий y(t ), а также влияние возмущающих воздействий f(t ). Для оценки эффективности решения задач управления вводятся так называемые показатели качества управления. Различают динамические показатели, определяющие качество переходного режима работы системы, к которым относятся количественные (численные) оценки быстродействия и колебательности системы, и точностные показатели, определяющие погрешность системы в установившемся режиме, т.е. по окончанию переходного процесса. К динамическим показателям относится время переходного процесса t _п и перерегулирование  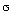, а к точностным - абсолютная погрешность стабилизации или слежения

                     . 

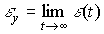1.4.2. Многоканальное управление. В многоканальных задачах управления выходом объекта служит векторная переменная (вектор выхода) y = y(t)= {y_j(t)} и, следовательно, векторными переменными являются также задающее воздействие (вектор задания) y*= y*(t) = {y*_j(t)} и рассогласование (вектор ошибок) 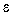 = 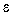(t)={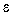 _j(t) }. Формулировка основных задач многоканального управления ( стабилизации, слежения и терминального управления ) практически не отличается от приведенной выше. Кроме них для многоканальных объектов возникает ряд специфических задач, среди которых выделим задачи декомпозиции и согласованного управления.

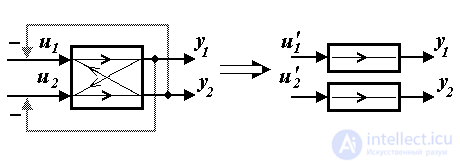
Рис. 1.21. Декомпозиция многоканальной системы

Задача декомпозиции заключается в устранении взаимного влияния каналов системы с целью сведения задачи управления многосвязным объектом к нескольким более простым одноканальным задачам. Решение задачи предусматривает создание дополнительных (искусственных) перекрестных связей между каналами системы, которые компенсируют нежелательное действие внутренних связей объекта управления (рис. 1.21). Это достигается с помощью соответствующих алгоритмов управления, т.е. выбора управляющих воздействий u_j.

Задача согласованного управления наоборот предусматривает организацию принудительного взаимодействия каналов с целью поддержания заданных функциональных соотношений (условий согласования) выходных переменных y_j(t) вида:

(1.8) 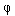                     (y₁ ,y₂ ,...y_m) = 0,

где 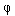 - заданная функция размерности m-1 . Решение также требует введения искусственных перекрестных связей (рис. 1.22), т.е. координации управляющих воздействий u_j.

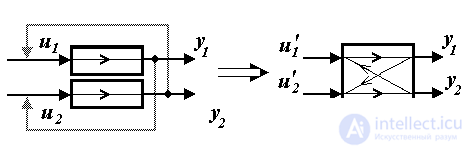
Рис. 1.22. Согласование выходных переменных

 

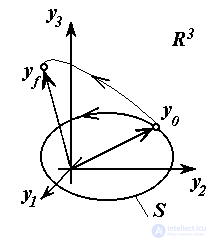Наиболее очевидные задачи терминального и согласованного управления возникают при управлении пространственным движением многозвенных механических объектов (роботов, станочных механизмов, транспортных средств). Здесь в качестве выходных переменных системы обычно выступают декартовы координаты y_j рабочей точки механизма в трехмерном физическом пространстве R³ или R² , а задача перемещения рабочей точки механизма из начального положения y₀={y_j0} в точку y_f={y_jf}относится к многоканальным терминальным задачам. Если при этом возникает необходимость следования определенной траектории движения S , то возникает задача согласования выходных переменных, в которой условия согласования (1.8) это не что иное, как уравнение S в физическом пространстве.

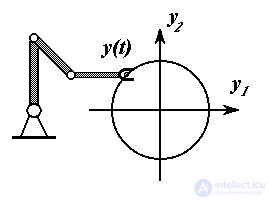
Пример 1.6. Так называемое контурное движение свата простейшего робота-манипулятора в плоскости R² осуществляется по отрезкам прямых и окружностей, заданной в виде

(1.9)                     

с ₁ y₁ + с ₂ y₂ +с = 0

или

(1.10)                      , 

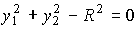соответственно. Эти уравнения и определяют условия согласования выходных переменных рассматриваемой многоканальной системы.

1.4.3. Задачи контроля. Вспомогательные задачи определения (идентификации) неизмеряемых переменных и неизвестных параметров системы относятся к задачам автоматического контроля. Это:

• задача наблюдения, т.е. оценивание неизмеряемых переменных состояния объекта в условиях действия шумов (фильтрация, наблюдение, предсказание, см. также п.1.1);
• задача идентификации параметров, т.е. оценивания неизвестных параметров системы (массо-инерционных, электрических и термодинамических и проч.).

 

Прочтение данной статьи про локальные задачи управления позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое локальные задачи управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про локальные задачи управления