Лекция
Привет, Вы узнаете о том , что такое временные характеристики линейных стационарных систем переходные процессы ы решения задач, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое временные характеристики линейных стационарных систем переходные процессы ы решения задач , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Система автоматического регулирования в процессе работы может находиться в одном из двух, качественно отличных друг от друга, состояниях: в установившемся или неустановившемся режимах.
Установившийся (нормальный) режим работы автоматической системы характеризуется неизменностью внешних условий функционирования системы.
Неустановившийся (переходный) режим работы возникает сразу же после воздействия на систему управляющего или возмущающего сигналов. Поведение регулируемой величины в неустановившемся режиме называется переходным процессом. Переходные процессы могут быть затухающими и незатухающими. При затухающем переходном процессе регулируемая величина стремится к своему состоянию в установившемся режиме.
В системе с не затухающим переходным процессом регулируемая величина либо неограниченно возрастает (чаще всего в виде расходящихся колебаний), либо остается в том же состоянии, что и в начале переходного процесса. Такая система никогда не приходит в заданный для нее установившийся режим и называется неустойчивой.
Типовые входные сигналы, используемые при исследовании автоматических систем
Для исследования переходных процессов автоматической системы нео6ходимо подать на вход системы такое воздействие, которое вывело бы ее из состояния покоя и в дальнейшем обеспечило свободное движение регулируемой величины. Такими входными воздействиями являются ступенчатая функция и импульсная ? – функция (функция Дирака) (рис. 4.1, рис. 4.2).
Единичная ступенчатая функция обозначается 1(t) и представляет собой выражение:
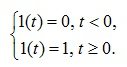(4.1)
Функция 1(t) непрерывна всюду, кроме точки t=0, где она терпит разрыв первого рода, Эта функция соответствует замыканию ключа, подающего напряжение 1 в. Изображение единичной функции по Лапласу имеет вид:
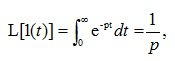(4.2)
Для записи произвольного ступенчатого сигнала используется выражение
x(t)=Al(t) (4.3)
где А – амплитуда сигнала.
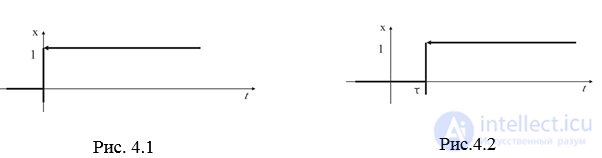
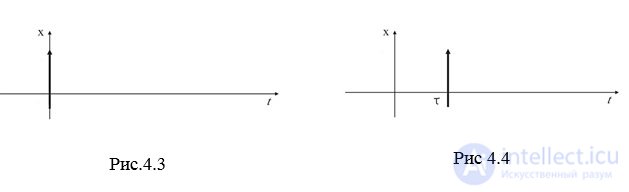
Импульсной ? – функцией называется функция, равная нулю всюду, кроме начала координат, где она равна бесконечности (рис. 4.3, рис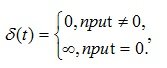. 4.4):
(4.4)
Интеграл от этой функции по любому интервалу, содержащему начало координат, равен единице т.е.
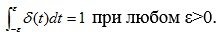(4.5)
Импульсная функция представляет собой математическую идеализацию предельно короткого импульса, площадь которого равна единице. Изображение импульсной функции по Лапласу имеет вид:
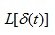(4.6)
Импульсная ? – функция является производной от единичной ступенчатой функции
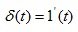(4.7)
Импульсная ? – функция обладает фильтрующим свойством.
Реакции автоматической системы на единичную ступенчатую функцию и импульсную функцию называются временными характеристиками системы, так как представляют собой процесс изменения регулируемой величины во времени.
Временные характеристики
Тип переходного процесса, качество регулирования и состояние автоматической системы в установившемся режиме, определяются по виду переходной и весовой функций (характеристик) системы.
Переходной характеристикой линейной автоматической системы называется ее реакция на воздействие единичной ступенчатой функции при нулевых начальных условиях.
Переходная характеристика обозначается h(t) и представляет собой переходный процесс, вызванный скачкообразным изменением входной величины. Она может быть определена при решении дифференциального уравнения обычным или операторным методом.
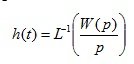(4.8)
Весовой функцией линейной автоматической системы называется ее реакция на импульсную ? - функцию при нулевых начальных условиях.
Весовая функция обозначается k(t) и представляет собой переходной процесс, вызванный мгновенным "ударным" воздействием короткого импульса на входе системы. Об этом говорит сайт https://intellect.icu . Весовая функция также находится решением дифференциального уравнения системы.
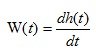- весовая функция (4.9)
При исследовании динамических свойств автоматической системы интерес представляют:
- поведение системы в начальный момент времени (сразу после приложения воздействия);
- характер изменения регулируемой величины в переходном режиме;
- поведение регулируемой величины при приближении к новому установившемуся состоянию;
- поведение регулируемой величины в установившемся режиме;
- длительность переходного процесса.
Информация об этом может быть получена в результате анализа весовой или переходной функций автоматической системы.
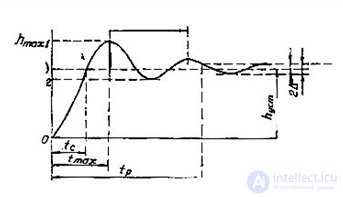
Рис. 4.5. Кривая переходной характеристики
1) Время регулирования tp –минимальное время, по истечению которого регулируемая величина будет оставаться в достаточно малой окрестности установившегося значения, т.е.
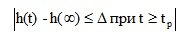(4.10)
где ? – постоянная величина, значение которой обычно принимается 5% от .
2) Абсолютная и относительная величины перерегулирования, определяющие отклонение переходной характеристики от установившегося значения.
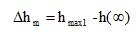(4.11)
и величина относительного отклонения, выражаемая в процентах,
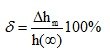(4.12)
3) Время первого согласования (быстродействие) tc, определяющее время первого достижения установившегося значения h(?).
4) Частота колебаний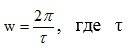 
– период колебаний переходной характеристики.
5) Число колебаний n, которое имеет переходная характеристика за время регулирования tp.
6) Время достижения первого максимума tmax.
В любой АСУ в результате воздействия возмущающих сил, с одной стороны, и восстанавливающего действия управляющего устройства, с другой, возникает переходный процесс: переход АСУ из одного состояния в другое. Рассмотрим различные типы переходного процесса (рис. 4.6).
Решение дифференциального уравнения описывает переходной процесс y(t), характер которого определяется коэффициентом. Рассмотрим переходные процессы, соответствующие различным значениям.
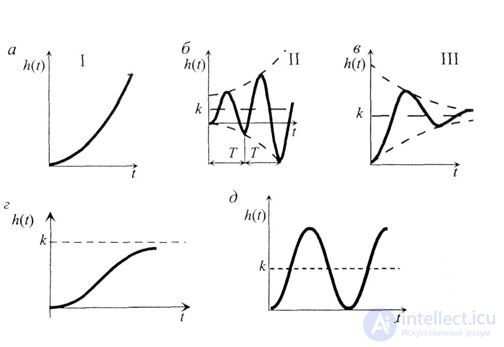
Рис. 4.6
4. ? > 1. Характеристика системы та же, что и в III случае, но переходный процесс монотонный (апериодический) (рис. 4.6, г).
5. ?= 0; В системе устанавливается периодическое движение, процесс называется колебательным незатухающим, система находится на границе устойчивости (рис. 4.6, д). Она является замкнутой (консервативной), автономной от внешней среды.
Все рассмотренные колебания (II, III и V случаи) относятся к классу свободных, их параметры А и ? зависят от начальных условий, т. е. от привнесенной энергии. Для случаев II и III функция h(t)?h(t+T), где Т- период колебаний, и следовательно, эти колебания непериодические. Периодические колебания наблюдаются только в случае V
Пример 1. Дано уравнение в дифференциальном виде:
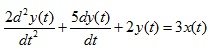
Определить переходную и весовую характеристики. Построить графики.
Решение:
Переходная характеристика определяется по формуле (4.8):
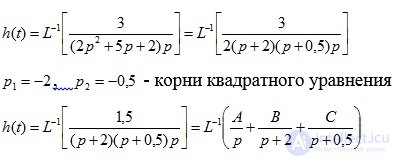
A, B, C определяем с помощью метода неопределенных коэффициентов
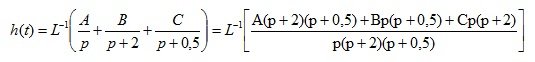
Приравняем между собой числители двух дробей
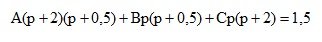
Весовая функция Лапласа
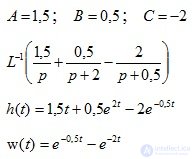
Внимание!
При решении используется метод неопределенных коэффициентов (из курса высшей математики). Метод неопределенных коэффициентов применяют при интегрировании рациональных дробей. Рациональной дробью называется дробь вида
,
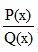где P(x) и Q(x) являются многочленами. Рациональная дробь называется правильной, если степень числителя P(x) ниже степени знаменателя Q(x); в противном случае дробь называют неправильной. Любая правильная рациональная
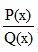дробь может быть единственным образом представлена в виде суммы простых рациональных дробей. Простые рациональные дроби:
Если при решении дифференциальных уравнений:
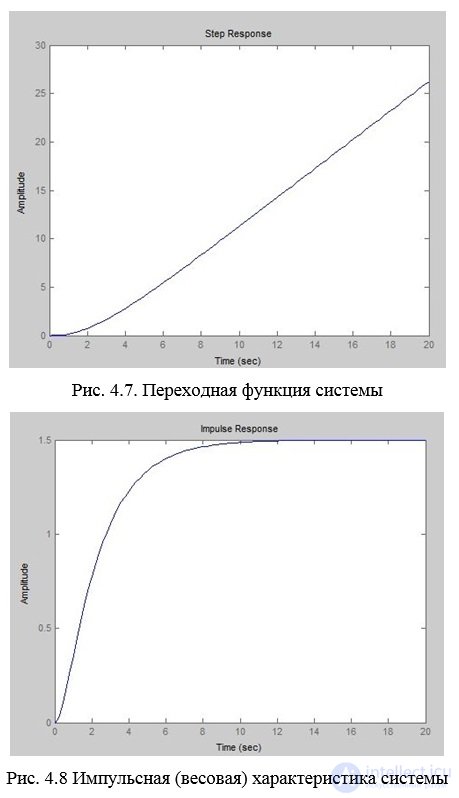
Вывод: По полученной переходной функции можно сделать вывод о том, что система неустойчива.
Пример 2. Задан оператор линейной стационарной системы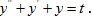 
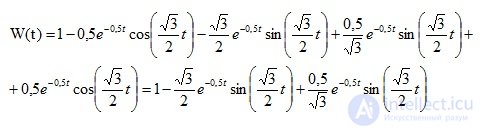
Вывод: По полученной переходной функции можно сделать вывод о том, что система неустойчива.
Прочтение данной статьи про временные характеристики линейных стационарных систем переходные процессы ы решения задач позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое временные характеристики линейных стационарных систем переходные процессы ы решения задач и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Из статьи мы узнали кратко, но содержательно про временные характеристики линейных стационарных систем переходные процессы ы решения задач
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления