Лекция
Сразу хочу сказать, что здесь никакой воды про тау, и только нужная информация. Для того чтобы лучше понимать что такое тау, теория автоматического управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Теория автоматического управле́ния ( тау ) — научная дисциплина, которая изучает процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.
Является составной частью технической кибернетики и предназначена для разработки общих принципов автоматического управления, а также методов анализа (исследования функционирования) и синтеза (выбора параметров) систем автоматического управления (САУ) техническими объектами.
Для этой теории имеет значение только характер преобразований сигналов объектами управления.
Впервые сведения об автоматах появились в начале нашей эры в работах Герона Александрийского «Пневматика» и «Механика», где описаны автоматы, созданные самим Героном и его учителем Ктесибием: пневмоавтомат для открытия дверей храма, водяной орган, автомат для продажи святой воды и др. Идеи Герона значительно опередили свой век и не нашли применения в его эпоху.
В Средние века значительное развитие получила имитационная «андроидная» механика, когда конструкторы-механики создали ряд автоматов, подражающих отдельным действиям человека, и, чтобы усилить впечатление, изобретатели придавали автоматам внешнее сходство с человеком и называли их «андроидами», то есть человекоподобными. В настоящее время подобные устройства называют роботами, в отличие от широко распространенных во всех сферах человеческой деятельности устройств автоматического управления, которые называют автоматами.
В XIII веке немецкий философ-схоласт и алхимик Альберт фон Больштадт построил робота для открывания и закрывания дверей.
Весьма интересные андроиды были созданы в XVII—XVIII веках. В XVIII веке швейцарские часовщики Пьер Дро и его сын Анри создали механического писца, механического художника и др. Прекрасный театр автоматов был создан в XVIII в. русским механиком-самоучкой Кулибиным. Его театр, хранящийся в Эрмитаже, помещен в «часах яичной фигуры».
В зачаточном виде многие положения теории автоматического управления содержатся в Общей теории (линейных) регуляторов, которая была разработана, в основном, в 1868—1876 годы в работах Максвелла и Вышнеградского. Основополагающими трудами Вышнеградского являются: «Об общей теории регуляторов», «О регуляторах непрямого действия». В этих работах можно найти истоки современных инженерных методов исследования устойчивости и качества регулирования.
Решающее влияние на развитие отечественной методологии исследований теории автоматического управления сыграли работы выдающегося советского математика Андрея Маркова (младшего), основоположника советской конструктивистской школы математики, автора работ по теории алгоритмов и математической логике. Эти исследования нашли применение в научной и практической деятельности академика Лебедева по военной тематике — автоматах управления торпедами и наведения орудий и устойчивости крупных энергосистем.
К началу XX века и в первом его десятилетии теория автоматического управления формируется как общенаучная дисциплина с рядом прикладных разделов.
Автоматика — отрасль науки и техники, охватывающая теорию и практику автоматического управления, а также принципы построения автоматических систем и образующих их технических средств.
Объект управления (ОУ) — устройство, физический процесс либо совокупность процессов, которыми необходимо управлять для получения требуемого результата. Взаимодействие с ОУ происходит путем подачи на его условный вход управляющего воздействия (которое корректирует процессы протекающие в ОУ), при этом на выходе получается измененный параметр (который является процессом-следствием).
Управление — воздействие (сигнал), подаваемое на вход объекта управления и обеспечивающее такое протекание процессов в объекте управления, которое обеспечит достижение заданной цели управления на его выходе.
Цель — желаемое протекание процессов в объекте управления и получение нужного изменения параметра на его выходе.
Объекты:
Система автоматического управления (САУ) включает в себя объект управления и устройство управления.
Устройство управления — совокупность устройств, с помощью которых осуществляется управление входами объекта управления.
Регулирование — частный случай управления, цель которого заключается в поддержании на заданном уровне одного или нескольких выходов объекта управления.
Регулятор — преобразует ошибку регулирования ε(t) в управляющее воздействие, поступающее на объект управления.
Задающее воздействие g(t) — определяет требуемый закон регулирования выходной величины.
Ошибка регулирования ε(t) = g(t) — y(t), разность между требуемым значением регулируемой величины и текущим ее значением. Если ε(t) отлична от нуля, то этот сигнал поступает на вход регулятора, который формирует такое регулирующее воздействие, чтобы в итоге с течением времени ε(t) = 0.
Возмущающее воздействие f(t) — процесс на входе объекта управления, являющийся помехой управлению.
Системы автоматического управления:
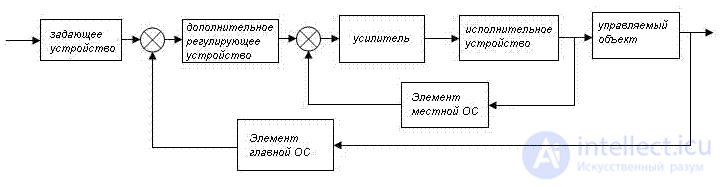
Типовая схема САУ
Функциональная схема элемента — схема системы автоматического регулирования и управления, составленная по функции, которую выполняет данный элемент.
Выходные сигналы — параметры, характеризующие состояние объекта управления и существенные для процесса управления.
Выходы системы — точки системы, в которых выходные сигналы могут наблюдаться в виде определенных физических величин.
Входы системы — точки системы, в которых приложены внешние воздействия.
Входные сигналы:
Системы:
Обратная связь — связь, при которой на вход регулятора подается действительное значение выходной переменной, а также заданное значение регулируемой переменной.
Управление по принципу отклонения управляемой переменной — обратная связь образует замкнутый контур. На управляемый объект подается воздействие, пропорциональное сумме (разности) между выходной переменной и заданным значением, так, чтобы эта сумма (разность) уменьшалась.
Управление по принципу компенсации возмущений — на вход регулятора попадает сигнал, пропорциональный возмущающему воздействию. Отсутствует зависимость между управляющим воздействием и результатом этого действия на объект.
Управление по принципу комбинированного регулирования — используется одновременно регулирование по возмущению и по отклонению, что обеспечивает наиболее высокую точность управления.
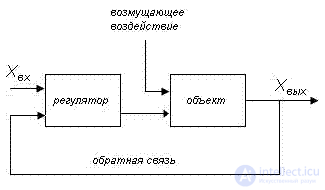
Принцип отклонения управляемой переменной в ТАУ
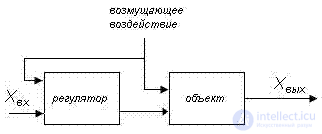
Принцип компенсации возмущений в ТАУ

Принцип комбинированного регулирования в ТАУ
По характеру управления:
По характеру действия:
По степени использования информации о состоянии объекта управления:
По степени использования информации о параметрах и структуре объекта управления:
По степени преобразования координат в САУ:
По виду математической модели преобразования координат:
По виду управляющих воздействий:
По степени участия человека:
По закону изменения выходной переменной:
По количеству управляемых и регулируемых переменных:
По степени самонастройки, адаптации, оптимизации и интеллектуальности:
По воздействию чувствительного (измерительного) элемента на регулирующий орган:
ИСАУ — это системы, которые позволяют проводить обучение, адаптацию или настройку за счет запоминания и анализа информации о поведении объекта, его СУ и внешних воздействий. Особенностью данных систем является наличие базы данных машины логического вывода, подсистемы объяснений и др.
База знаний — формализованные правила в виде логических формул, таблиц и т. п. ИСУ используется для управления плохо формализованными или сложными техническими объектами.
Класс ИСУ соответствует признакам:
Если ИСУ удовлетворяет всем 5-ти признакам, то она интеллектуальна в «большом», иначе в «маленьком» смысле.
Статистические характеризуются набором статистических параметров и функций распределения. Для их исследования используются методы математической статистики.
Адаптивные используют для описания объекта управления детерминированно-стохастические методы.
Wэ(p) = W1(p)W2(p)…Wn(p) = (p)
Wэ(p) = W1(p) + W2(p) + … + Wn(p) = (p)
Решая данную систему уравнений, получим следующие результаты:
Система в пространстве состояний задается в виде:
Система имеет m входов u(t), l выходов y(t), n состояний x(t), n>= max(m, l), A,B,C,D — числовые матрицы соответствующей размерности nxn, nxm, lxn, lxm..
Пусть I — единичная матрица размерности nxn, тогда:
pI X(p) — A X(p) = B U(p)
(pI — A)X(p) = BU(p)
x(0) = 0
X(p)=Wxu(p)U(p); Wxu(p) = (pI — A)^{-1)B
Y(p)=Wyu(p)U(p); Wyu(p)=C (pI — A)^{-1) B + D
Пусть САУ регулируется и описывается нелинейным уравнением
Причем нелинейность несущественна, то есть эту функцию можно разложить в ряд Тейлора в окрестности стационарной точки, например, при внешнем возмущении f = 0.
Уравнение этого звена в установившемся режиме выглядит следующим образом:
, начальные точки, производные отсутствуют.
Тогда, разлагая нелинейную функцию в ряд Тейлора, получим:
— остаточный член
От нелинейной записи перешли в линейную. Об этом говорит сайт https://intellect.icu . Перейдем к операторному уравнению:
САУ управляема (полностью управляема), если она может быть переведена из любого начального состояния x0(t) в другое произвольное состояние x1(t) в произвольный момент времени путем приложения кусочно-непрерывного воздействия U(t)∈[t0;t1].
САУ наблюдаема (полностью наблюдаема), если все переменные состояния x(t) можно определить по выходному (измеряемому) воздействию y(t).
Устойчивость — свойство САУ возвращаться в заданный или близкий к нему установившийся режим после какого-либо возмущения. Устойчивая САУ — система, в которой переходные процессы являются затухающими.
— операторная форма записи линеаризированного уравнения.
y(t) = yуст(t)+yп = yвын(t)+yсв
yуст(yвын) — частное решение линеаризированного уравнения.
yп(yсв) — общее решение линеаризированного уравнения как однородного дифференциального уравнения, то есть
САУ устойчива, если переходные процессы уn(t), вызываемые любыми возмущениями, будут затухающими с течением времени, то есть при
Решая дифференциальное уравнение в общем случае, получим комплексные корни pi, pi+1 = ±αi ± jβi
Каждой паре комплексно-сопряженных корней соответствует следующая составляющая уравнения переходного процесса:
, где
,
Из полученных результатов видно, что:
Для определения устойчивости системы строятся таблицы вида:
| Коэффициенты | Строки | столбец 1 | столбец 2 | столбец 3 |
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
Для устойчивости системы необходимо, чтобы все элементы первого столбца имели положительные значения; если в первом столбце присутствуют отрицательные элементы — система неустойчива; если хотя бы один элемент равен нулю, а остальные положительны, то система на границе устойчивости.
— определитель Гурвица
Теорема: для устойчивости замкнутой САУ необходимо и достаточно, чтобы определитель Гурвица и все его миноры были положительны при
Заменим , где ω — угловая частота колебаний, соответствующих чисто мнимому корню данного характеристического полинома.
Критерий: для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы кривая Михайлова, построенная в координатах , проходила последовательно через n квадрантов.
Рассмотрим зависимость между кривой Михайлова и знаками его корней (α>0 и β>0)
1) Корень характеристического уравнения — отрицательное вещественное число
Соответствующий данному корню сомножитель
2) Корень характеристического уравнения — положительное вещественное число
Соответствующий данному корню сомножитель
3) Корень характеристического уравнения — комплексная пара чисел с отрицательной вещественной частью
Соответствующий данному корню сомножитель
, где
4) Корень характеристического уравнения — комплексная пара чисел с положительной вещественной частью
Соответствующий данному корню сомножитель
, где
Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой или логарифмических частотных характеристик разомкнутой системы.
Пусть разомкнутая система представлена в виде полинома
тогда сделаем подстановку и получим:
Для более удобного построения годографа при n>2 приведем уравнение (*) к «стандартному» виду:
При таком представлении модуль A(ω) = | W(jω)| равен отношению модулей числителя и знаменателя, а аргумент (фаза) ψ(ω) — разности их аргументов. В свою очередь, модуль произведения комплексных чисел равен произведению модулей, а аргумент — сумме аргументов.
Модули и аргументы, соответствующие сомножителям передаточной функции:
| Сомножитель | ||
|---|---|---|
| k | k | 0 |
| p | ω | |
|
|
||
|
|
После чего построим годограф для вспомогательной функции , для чего будем изменять
При , а при
(так как n<m и
)
Для определения результирующего угла поворота найдем разность аргументов числителя и знаменателя
Полином числителя вспомогательной функции имеет ту же степень, что и полином ее знаменателя, откуда следует , следовательно, результирующий угол поворота вспомогательной функции равен 0. Это означает, что для устойчивости замкнутой системы годограф вектора вспомогательной функции не должен охватывать начало координат, а годограф функции
, соответственно, точку с координатами
В условиях эксплуатации параметры системы по тем или иным причинам могут меняться в определенных пределах (старение, температурные колебания и т.п.). Эти колебания параметров могут привести к потере устойчивости системы, если она работает вблизи границы устойчивости. Поэтому стремятся спроектировать систему так, чтобы она работала вдали от границы устойчивости. Степень этого удаления называют запасом устойчивости.
Необходимость запаса устойчивости определяется следующими условиями:
Частотный критерий Найквиста применим, главным образом, когда трудно получить фазовые характеристики экспериментально. Однако вычисление АФХ, особенно частотных, сложнее, чем построение кривых Михайлова. Кроме того, расположение АФЧХ не дает прямого ответа на вопрос: устойчива ли система, то есть требуется дополнительное исследование на устойчивость системы в разомкнутом состоянии.
Критерий Михайлова применяется для систем любого порядка, в отличие от критерия Рауса. Применяя частотный критерий Найквиста и критерий Михайлова, характеристические кривые можно строить постепенно, с учетом влияния каждого звена, что придает критериям наглядность и решает задачу выбора параметров системы из условия устойчивости.
Карьера инженера по системам управления начинается со степени бакалавра и может продолжаться в колледже. Дипломы инженера-контролера хорошо сочетаются со степенью инженера-электрика или машиностроителя. Инженеры по контролю обычно получают работу в области технического менеджмента, где они обычно возглавляют междисциплинарные проекты. Есть много возможностей трудоустройства в аэрокосмических компаниях, производственных компаниях, автомобильных компаниях, энергетических компаниях и государственных учреждениях. Некоторые места, где нанимают инженеров по контролю, включают такие компании, как Rockwell Automation, NASA, Ford и Goodrich. Инженеры по контролю могут зарабатывать 66 тысяч долларов в год от Lockheed Martin Corp. Они также могут зарабатывать до 96 тысяч долларов в год от General Motors Corporation.
Согласно опросу Control Engineering , большинство людей, ответивших на вопросы, были инженерами по контролю в различных формах своей карьеры. Не так много профессий, которые можно отнести к категории «инженер по управлению», большинство из них - это конкретные карьеры, которые имеют небольшое сходство с всеобъемлющей карьерой инженера управления. Большинство инженеров по системам управления, принявших участие в опросе в 2019 году, являются проектировщиками систем или продуктов, или даже инженерами по контролю или приборам. Большинство работ связано с технологическим проектированием, производством или даже техническим обслуживанием, они представляют собой разновидности техники управления
А как ты думаешь, при улучшении тау, будет лучше нам? Надеюсь, что теперь ты понял что такое тау, теория автоматического управления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления