Лекция
Привет, Вы узнаете о том , что такое переходные процессы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое переходные процессы, характеристики моделей вход-выход , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Будем рассматривать линейные стационарные динамические системы, описываемые на интервале времени [0 , tf ), где tf > 0, дифференциальным уравнением [M1] с начальными условиями t(0)=0, 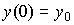 ,
, 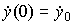 ,...,
,...,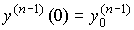 и достаточно гладким входным воздействием u(t).
и достаточно гладким входным воздействием u(t).
Решением дифференциального уравнения [M1] называется функция
(2.18) 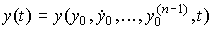 ,
,
которая при t= 0 удовлетворяет начальным условиям, а для любых 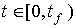 уравнению [M1]. С этим определением тесно связаны понятие фазовых переменных системы, к которым относятся функции,
уравнению [M1]. С этим определением тесно связаны понятие фазовых переменных системы, к которым относятся функции, 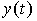 ,
,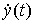 ,...,
,...,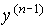 (t) , удовлетворяющие уравнению [M1], и понятие переходного процесса. Переходным процессом называют процесс изменения во времени различных переменных системы (фазовых и входных переменных, отклонений и т.д.), в ходе которого система изменяет свое состояние. Переходный процесс может быть получен в аналитическом или графическом виде. К графическим формам переходного процесса относятся
(t) , удовлетворяющие уравнению [M1], и понятие переходного процесса. Переходным процессом называют процесс изменения во времени различных переменных системы (фазовых и входных переменных, отклонений и т.д.), в ходе которого система изменяет свое состояние. Переходный процесс может быть получен в аналитическом или графическом виде. К графическим формам переходного процесса относятся
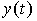 ,
, 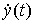 ,..., u(t ) и т.д.;
,..., u(t ) и т.д.;
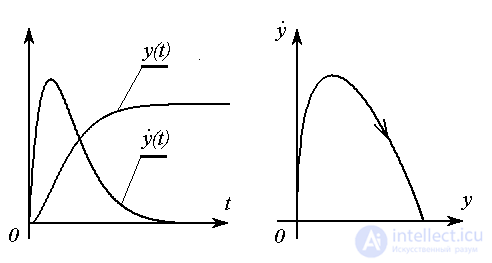
Рис . 2.3 . Переходные процессы: временные диаграммы и фазовая траектория
Решение 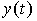 может быть представлено в виде
может быть представлено в виде
(2.19) 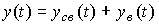 ,
,
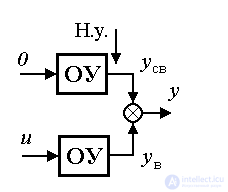
т.е. содержит две составляющие. Вынужденная составляющая  (t) соответствует переходному процессу системы [ М1 ] при начальных условиях:
(t) соответствует переходному процессу системы [ М1 ] при начальных условиях: 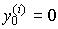 и является реакцией системы на входное воздействие u(t). Свободная составляющая
и является реакцией системы на входное воздействие u(t). Свободная составляющая  (t), или переходный процесс автономной системы, соответствует решениям однородного дифференциального уравнения [ М1 a] и зависит от начальных условий
(t), или переходный процесс автономной системы, соответствует решениям однородного дифференциального уравнения [ М1 a] и зависит от начальных условий 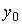 ,
, 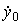 ,...,
,...,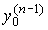
Поведение автономной системы и свободная составляющая переходного процесса  (t ) зависит от полюсов системы, т.е. корней
(t ) зависит от полюсов системы, т.е. корней 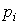 характеристического уравнения
характеристического уравнения 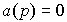 (см. также п. 3.3). Корни принимают вещественные значения
(см. также п. 3.3). Корни принимают вещественные значения
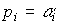 ,
,
или представлены комплексно-сопряженными парами:
 ,
,
где α i=Re pi - вещественная часть корня,  - коэффициент мнимой части.
- коэффициент мнимой части.

Рис. 2.4. Полюсы системы
Для случая неравных корней свободная составляющая определяется выражением:
(2.20)  ,
,
где 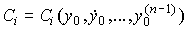 - неопределенные коэффициенты,
- неопределенные коэффициенты, 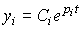 - свободные колебания системы, или моды.
- свободные колебания системы, или моды.
Вещественному корню 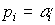 соответствует апериодическая составляющая переходного процесса
соответствует апериодическая составляющая переходного процесса
(2.21) 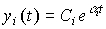 ,
,
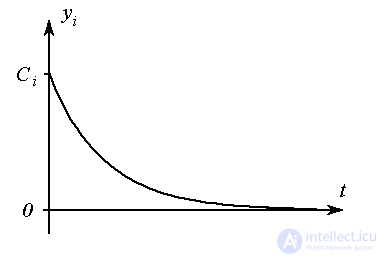
Рис. 2.5. Апериодический процесс
Паре комплексно-сопряженных корней характеристического уравнения соответствует колебательная составляющая
(2.22) 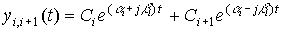
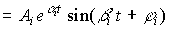 ,
,
где 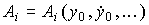 - амплитуда,
- амплитуда, 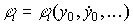 - фаза колебаний,
- фаза колебаний, 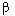 i - угловая частота.
i - угловая частота.
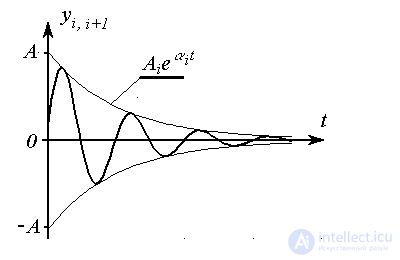
Рис. 2.6. Колебательный процесс
Если среди корней характеристического уравнения имеются равные, то выражение (2.20) не справедливо. Так, паре равных вещественных корней
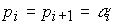
соответствует апериодическая составляющая переходного процесса вида
(2.23)  .
.
Для нахождения частного решения y св (t ), соответствующего заданным значениям начальных условий 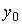 ,
, 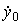 ,...,
,...,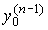 и значений Ci в формуле (2.20) используется метод неопределенных коэффициентов . В соответствии с методом из формулы (2.20) следует получить общие выражения для фазовых переменных
и значений Ci в формуле (2.20) используется метод неопределенных коэффициентов . В соответствии с методом из формулы (2.20) следует получить общие выражения для фазовых переменных 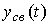 ,
,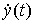 ,...,
,..., 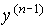 и при t= 0 записать n алгебраических уравнений
и при t= 0 записать n алгебраических уравнений
(2.24) 
Уравнения содержат n неизвестных С i , которые находятся одним из известных методов. Об этом говорит сайт https://intellect.icu . Например, можно переписать уравнение (2.24) в векторно-матричной форме
 ,
,
где 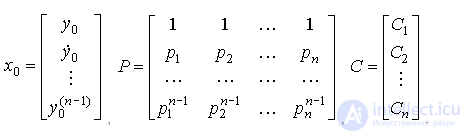
и найти вектор-столбец неизвестных коэффициентов как
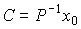 .
.
Если при некоторых значениях начальных условий имеет место тождество
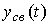 =y*,
=y*, 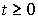 ,
,
где y*= const , то значение y=y* называется равновесным значением выходной переменной (или положением равновесия ) автономной системы [M1а]. В положении равновесия можно записать
(2.25) 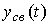 = y*,
= y*, 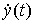 ,...,
,...,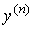 .
.
После подстановки (2.25) в уравнение [M1а] найдем
(2.26) an y*=0.
При условии , что an &nequal; 0 , получаем, что единственным положением равновесия рассматриваемой системы является начало координат
(2.27) y*= 0,
а при an = 0 находим бесчисленное множество равновесных значений.
Замечание 2 .1 . При условии, что вещественная часть 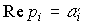 некоторого вещественного или комплексного корня pi строго отрицательна, т.е.
некоторого вещественного или комплексного корня pi строго отрицательна, т.е.
(2.28) 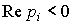 ,
,
соответствующая составляющая переходного процесса со временем затухает:
 .
.
Если условие (2.28) имеет место для всех 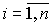 , то затухающей является вся свободная составляющая:
, то затухающей является вся свободная составляющая:
(2.29) 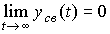 ,
,
причем предельное значение выходной переменной в точности совпадает с положение равновесия автономной системы y* = 0.
Вынужденная составляющая переходного процесса зависит от входного воздействия и может быть аналитически определена только для ряда частных случаев, соответствующих некоторым типовым входным сигналам. Наиболее распространенными сигналами являются единичный скачек, 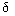 -функция и гармоническое входное воздействие.
-функция и гармоническое входное воздействие.
Рассмотрим реакцию систему на единичную ступенчатую функцию (единичный скачок)
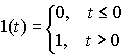 ,
,
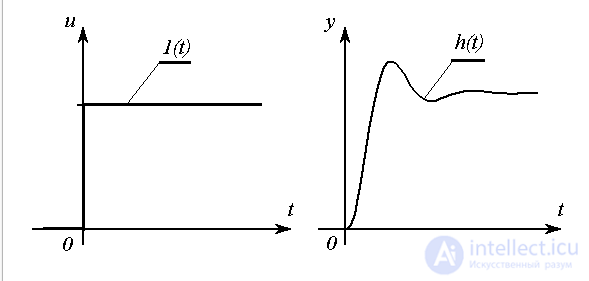
Рис. 2.7. Единичный скачек и переходная функция
Вынужденная составляющая 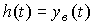 решения
решения 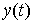 при воздействии на вход системы [M1] единичной ступенчатой функции
при воздействии на вход системы [M1] единичной ступенчатой функции 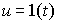 называется переходной функцией (характеристикой) системы, т.е.
называется переходной функцией (характеристикой) системы, т.е.
(2.30) 
Рассмотрим реакцию систему на единичную импульсную функцию (дельта-функцию) 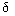 (t ). Последняя определяется как
(t ). Последняя определяется как
(2.31) 
или импульс бесконечно большой амплитуды A и бесконечно малой длительности  , удовлетворяющий условию
, удовлетворяющий условию
(2.32) 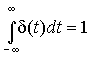 .
.

Рис. 2.8. Дельта-функция и весовая функция
Вынужденная составляющая 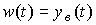 решения
решения 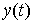 при воздействии на вход системы [M1] импульсной функции
при воздействии на вход системы [M1] импульсной функции  называется весовой функцией (характеристикой) системы, т.е.
называется весовой функцией (характеристикой) системы, т.е.
(2.33) 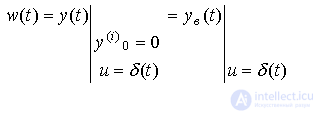
Отметим, что, учитывая определение (2.33) нетрудно получить
(2.34) 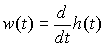 .
.
Для произвольного входного воздействия  вынужденная составляющая переходного процесса системы [M1] может быть найдена по формуле (интеграл свертки)
вынужденная составляющая переходного процесса системы [M1] может быть найдена по формуле (интеграл свертки)
(2.35)  .
.
В частном случае, когда 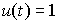 (t), в силу свойства (2.34), найдем
(t), в силу свойства (2.34), найдем
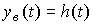 .
.
Отметим, что в общем случае нахождение вынужденной составляющей переходного процесса с помощью интегральных выражений типа (2.35) (см. также (2.42) в п. 3.2.1) вызывает затруднение. Значительно более простой задачей является нахождение установившейся составляющей переходного процесса.
Движение системы, рассматриваемое при достаточно больших значениях t (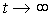 ), называется установившимся режимом. Соответственно, установившейся составляющей переходного процесса
), называется установившимся режимом. Соответственно, установившейся составляющей переходного процесса  называется вынужденная составляющая
называется вынужденная составляющая 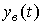 при
при 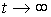 , т.е.
, т.е.
(2.36) 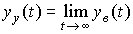 .
.
Функция 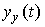 является частным решение уравнения [ М1 ] , полученном при определенных (обычно, ненулевых) начальных условиях и зависящим от его правой части, т.е. входного воздействия
является частным решение уравнения [ М1 ] , полученном при определенных (обычно, ненулевых) начальных условиях и зависящим от его правой части, т.е. входного воздействия  .
.
Замечание 2.2. Часто используется следующая форма представления решения системы [M1]:
(2.37)  ,
,
где 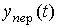 - переходная составляющая, или общее решение уравнения [ М1 ] , которое может быть найдено в форме аналогичной ( 2.20 ), т.е.
- переходная составляющая, или общее решение уравнения [ М1 ] , которое может быть найдено в форме аналогичной ( 2.20 ), т.е.
(2.38) 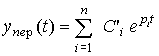 ,
,
где Ci' - постоянные коэффициенты.

Рис. 2.9. Переходные процессы и установившаяся составляющая
При условии, что для всех значений pi выполняется 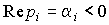 (см. замечание 2.2), свободная составляющая x св (а также
(см. замечание 2.2), свободная составляющая x св (а также 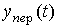 ) затухает, т.е. имеет место выражение (2.29). Тогда
) затухает, т.е. имеет место выражение (2.29). Тогда
(2.39) 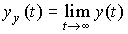 ,
,
т.е. установившаяся составляющая соответствует переходному процессу системы в установившемся режиме. С другой стороны, если одна из мод системы yi(t ), а следовательно и свободная составляющая в целом неограниченно возрастают, то предела (2.39) не существует, и понятие установившегося режима теряет смысл.
Типовые частные решения линейного уравнения [M1], соответствующие установившимся составляющим переходного процесса при воздействии на систему типовых входных сигналов u(t ), находятся по известным правилам:
| u(t) | y у (t) |
| U0 | Y0 |
| U0+U1t | Y0+Y 1t |
U0 sin 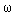 0t 0t |
Ysin ( 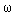 0t+ 0t+ 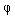 ) ) |
где U0, U1 ,Y0,Y1 , 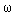 ; 0 ,
; 0 , 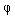 - постоянные.
- постоянные.
Наиболее важный частный случай решения системы [М1] соответствует постоянному входному воздействию 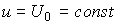 и установившейся составляющей
и установившейся составляющей
(2.40) 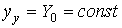 .
.
Пусть свободная составляющая системы затухает, т.е. имеет место свойство (2.39) и, следовательно,
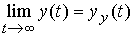 .
.
Последняя формула показывает, что при достаточно больших t (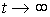 ) в системе отсутствует движение, т.е. имеет место статический режим работы.
) в системе отсутствует движение, т.е. имеет место статический режим работы.
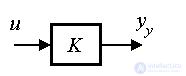
Решение уравнения (2.39) в статическом режиме ищется в виде
(2.41) 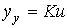 ,
,
где 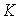 - неопределенный коэффициент. С учетом того, что при
- неопределенный коэффициент. С учетом того, что при 
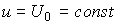 , запишем
, запишем
(2.42) 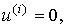
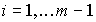 ,
,
а из уравнения (2.41) найдем, что
(2.43) 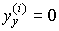 ,
, 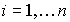 .
.
После подстановки (2.41)-(2.43) в [М1] получим простое алгебраическое выражение
(2.44) 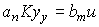 .
.
Пусть 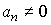 . Тогда неопределенный коэффициент K находится как
. Тогда неопределенный коэффициент K находится как
(2.45)  .
.
При 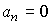 получим
получим 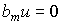 , где (см. п. 2.1)
, где (см. п. 2.1)  , т.е. в этом случае ( 2.44 ) не является частным решением уравнения [M1].
, т.е. в этом случае ( 2.44 ) не является частным решением уравнения [M1].
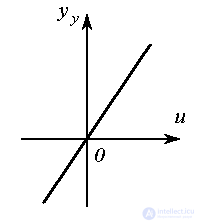
Зависимость установившейся составляющей (выходной переменной после окончания переходного процесса)  от величины входного сигнала
от величины входного сигнала  =const называется статической характеристикой динамической системы. Для линейных систем вида [M1] статическая характеристика представлена уравнением прямой (2.41), где постоянная
=const называется статической характеристикой динамической системы. Для линейных систем вида [M1] статическая характеристика представлена уравнением прямой (2.41), где постоянная 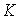 , рассчитываемая по формуле (2.45), называется коэффициентом передачи или статическим коэффициентом системы.
, рассчитываемая по формуле (2.45), называется коэффициентом передачи или статическим коэффициентом системы.
Система [M1], для которой  и следовательно существует статическая характеристика называется статической системой.
и следовательно существует статическая характеристика называется статической системой.
Астатической называется система, для которой 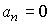 и следовательно, не существует статической характеристики, а установившийся режим невозможен.
и следовательно, не существует статической характеристики, а установившийся режим невозможен.
Определение статической характеристики сводится к элементарной операции нахождению статического коэффициента K
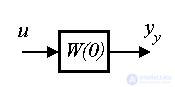
по формуле (2.45), где an и bm - соответствующие коэффициенты дифференциального уравнения [М1]. Однако статическая характеристика может быть получена и из операторной формы [М2] или [M3]. Сопоставляя (2.45) и [ М3 ] , найдем
(2.46) 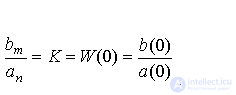 .
.
Следовательно, в статическом режиме система описывается уравнением
(2.47)  .
.
Замечание 2.3. По аналогии с определением положения равновесия автономной системы, можно ввести понятие равновесия возмущенной системы (2.40) при постоянном входном воздействии 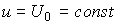 , т.е. положения, в котором выполняется тождество
, т.е. положения, в котором выполняется тождество
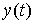 = y*,
= y*, 
и, следовательно,
(2.48) 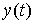 = y*,
= y*, 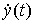 ,...,
,...,  .
.
Нетрудно показать, что равновесное значение выходной переменной y* в точности совпадает с установившимся значением, т.е.
(2.49) 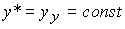 .
.
В частном случае при u=0 получаем автономную систему [M1а] и равновесное положение  .
.
Прочтение данной статьи про переходные процессы позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое переходные процессы, характеристики моделей вход-выход и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления
Комментарии
Оставить комментарий
Математические основы теории автоматического управления
Термины: Математические основы теории автоматического управления