18 Вычисление линейных интегральных оценок

Привет, Вы узнаете о том , что такое вычисление линейных интегральных оценок, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вычисление линейных интегральных оценок , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.

Рассмотрим проблему вычисления интеграла линейной интегральной оценки. Можно сначала решить аналитически дифференциальные уравнения, описывающие систему, долее определить ошибку регулирования, затем подставить выражение для ошибки в интеграл линейной оценки и, взяв его, получить выражение для .

Но можно поступить и иначе.

Пусть свободное движение ошибки регулирования системы описывается уравнением

(1)

Проинтегрируем это уравнение –

После интегрирования получаем –

(2)

Подстановки верхнего предела дают члены следующего вида –

(3)

так как все производные ошибки в установившемся режиме обращаются в ноль.

Подстановки нижнего предела дают члены вида –

(4)

которые являются начальными условиями уравнения (1).

Подставив (3) и (4) в (2), получим

(5)

А так как

,

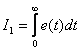окончательно получаем

(6)

Решая (6) относительно 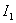, получим выражение для вычисления линейной интегральной ошибки –

(7)

Теперь мы может определить 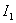 по коэффициентам характеристического уравнения системы и начальным условиям переходного процесса ошибки.

Для синтеза систем, определения параметров минимизирующих , следует воспользоваться обычными методами исследования функций на экстремум. Следовательно, если мы хотим определить параметр системы, на пример, параметр 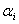, обеспечивающий 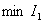, необходимо решить относительно параметра  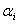следующее уравнение –

.

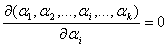Рассмотрим несколько примеров использования линейной интегральной оценки.

Пример

Система имеет характеристическое уравнение

(8)

Определим выражение для 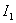, если начальные условия имеют вид –

.

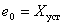Определим значение параметра 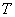, при котором интегральная оценка имеет минимум.

Решение

Обозначим –

.

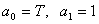Используем для нахождения  выражение (7) –

(9)

Из рассмотрения (9) получаем, что 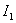 в этом случае не имеет экстремума, а меньшее значение интегральной ошибки мы будем получать при меньшем значении 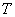. Об этом говорит сайт https://intellect.icu . Действительно, ведь уравнение (8) является характеристическим уравнением апериодического звена, параметр  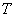– это постоянная времени. Переходный процесс для двух разных постоянных времени будет иметь вид, показанный на рис. 1.

Рис. 1

Пример

Система имеет характеристическое уравнение

.

Определим выражение для 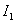, если начальные условия имеют вид –

.

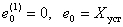Определим значение параметра 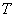, при котором интегральная оценка имеет минимум.

Решение

Обозначим –

.

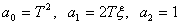Используем для нахождения 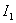 выражение (7) –

.

Если 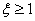, то процессы монотонные,  обеспечивается при наименьших 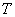 и 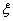. Если , то уменьшение коэффициента затухания уменьшает линейную интегральную оценку, но это приводит к ухудшению переходного процесса, повышению его колебательности.

    При колебательных процессах в системах линейная интегральная оценка дает значительную погрешность. При этом минимум оценки может соответствовать процессу с большим числом колебаний со значительной амплитудой, малым быстродействием, так как, по сути, в оценке происходит сложение положительных и отрицательных областей площади под интегральной кривой. Это иллюстрируют рис. 2 и 3, показывая два процесса, которые могут иметь одно и то же значение линейной интегральной оценки.

Рис. 2

Рис. 3

И так как форма переходного процесса при анализе системы автоматического управления часто заранее неизвестна, то применять линейные интегральные оценки на практике нецелесообразно.

Можно попытаться использовать интеграл от модуля ошибки следующего вида –

(10)

На рис. 4 показан примерный вид кривых изменения ошибки и ее модуля. Но аналитическое вычисление интеграла от модуля ошибки по математической модели системы оказалось весьма громоздким, поэтому эта оценка широкого распространения не получила.

Рис. 4

 

Квадратичная интегральная оценка

 

В большинстве случаев, при возможности возникновения в системе колебательного переходного процесса, используют квадратичную интегральную оценку, которая имеет следующий вид –

(11)

Оценка  не зависит от знака отклонений ошибки, а значит и от формы переходного процесса, монотонный, апериодический или колебательный характер он будет иметь. На рис. 5 и 6 показан примерный вид кривых изменения ошибки и квадрата ошибки.

Рис. 5

 

Рис. 6

Рассмотрим процедуру вычисления квадратичной оценки по математической модели системы. Система управления представляется в виде, показанном на рис. 7.

Рис. 7

Изображение по Лапласу сигнала на выходе системы имеет вид –

(12)

где  - изображение по Лапласу единичной ступенчатой функции – входного сигнала системы.

Для системы автоматического управления, математическая модель которой приведена к виду (12), интегральная квадратичная ошибка определяется по следующему выражению –

(13)

где

(14)

в  все элементы с индексами меньше 0 и больше 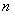 заменяются 0.

Определители 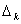 в (13), где 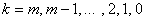, получаются заменой в определителе  (14) (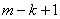)-го столбца столбцом следующего вида –

.

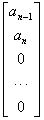Коэффициенты  в выражении (13) определяются следующим образом –

(15)

при определении  коэффициенты, индексы которых меньше 0 и больше , заменяются 0.

Контрольные вопросы и задачи

1. Какие параметры математической модели объекта требуются для вычисления линейной интегральной оценки?

2. Почему нельзя использовать линейную интегральную оценку в случае колебательного характера переходных процессов?

3. Какие интегральные оценки целесообразно использовать в том случае если в системе возможно наличие колебательных переходных процессов?

4. Дайте определение квадратичной интегральной оценке переходного процесса.

5. При минимизации квадратичной оценки, к какому виду стремится переходный процесс?

6. Какие параметры математической модели объекта требуются для вычисления квадратичной интегральной оценки?

7. Объект управления описывается передаточной функцией –

.

Вычислите линейную интегральную оценку переходного процесса при начальном значении ошибки .

Ответ:

Линейная интегральная оценка .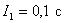

1. Объект управления описывается передаточной функцией –

.

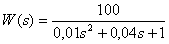Вычислите линейную интегральную оценку переходного процесса при начальном значении ошибки .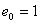

Ответ:

Линейная интегральная оценка .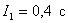

Прочтение данной статьи про вычисление линейных интегральных оценок позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое вычисление линейных интегральных оценок и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математические основы теории автоматического управления

Из статьи мы узнали кратко, но содержательно про вычисление линейных интегральных оценок

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.