Лекция
Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x.
Обозначение: y = f(x)
Независимая переменная x – аргумент функции f.
Число y, соответствующее x – значение функции f в точке x.
График функции — это геометрическое представление зависимости между аргументом (независимой переменной) и значением функции (зависимой переменной). Чаще всего графики строятся на плоскости, где одна ось соответствует аргументу функции, а другая — ее значению.
График функции f – множество всех точек (x; y) координатной плоскости, где y=f(x), а x «пробегает» всю
область определения функции f.
Графики элементарных функций
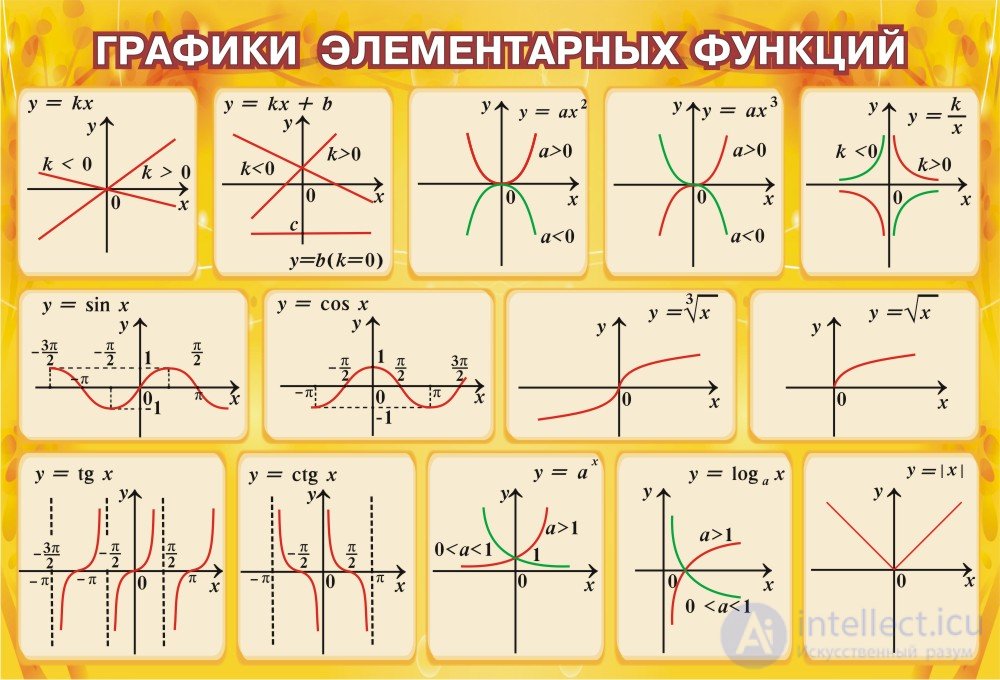
Аргумент и значение функции: Аргумент функции — это входное значение, которое подставляется в функцию, а значение функции — это результат ее вычисления. Например, в функции y=f(x)) переменная x является аргументом, а y — значением функции.
Область определения функции: Это множество всех значений аргумента, для которых функция определена. Для построения графика важно учитывать эту область, так как вне ее значения функции могут быть неопределенными.
Область значений функции: Это множество всех возможных значений, которые может принимать функция при всех допустимых значениях аргумента.
Чтобы построить график функции y=f(x), нужно:
Область определения функции – множество значений x, для которых выполнимы действия, указанные в правиле f.
Обозначается: ООФ или D(f).
С геометрической точки зрения ООФ есть проекция графика этой функции на ось ОХ.

Область значений функции – множество значений функции f(x), которые она принимает при изменении x на ООФ.
Обозначается: ОЗФ или E(f).
С геометрической точки зрения ОЗФ – проекция графика на ось OY.

Функция f называется четной, если для любых x из ООФ
f(-x) = f(x)
График четной функции симметричен относительно оси OY.
Функция f называется нечетной, если для любых x из ООФ f(-x) = - f(x)
График нечетной функции симметричен относительно начала координат.
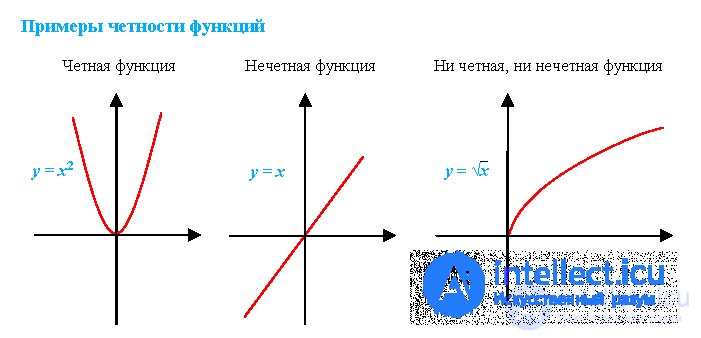
Алгоритм определения четности функции одной переменной

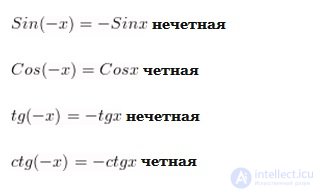
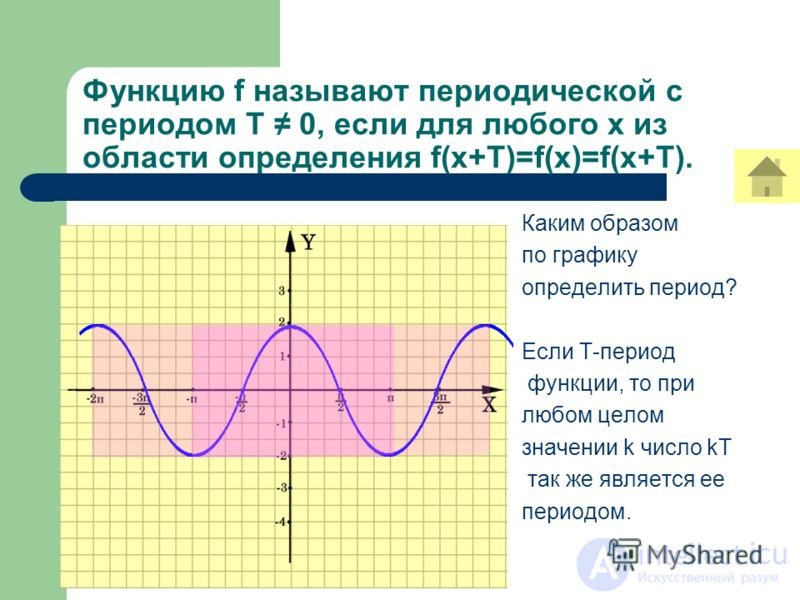
Функция называется периодической с периодом Т ≠ 0, если для любого x из ООФ
f(x + T) = f(x) = f(x - T).
Для построения графика периодичностью функции с периодом T достаточно провести построение на отрезке длиной T и полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси OX (n – любое натуральное число).

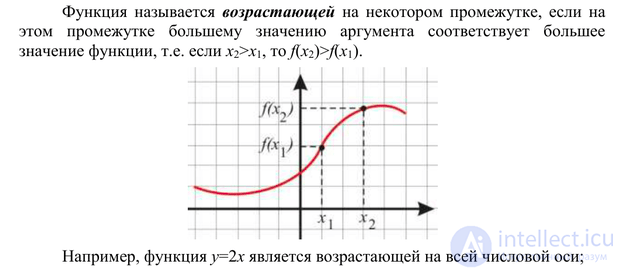
Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) > f(x1).
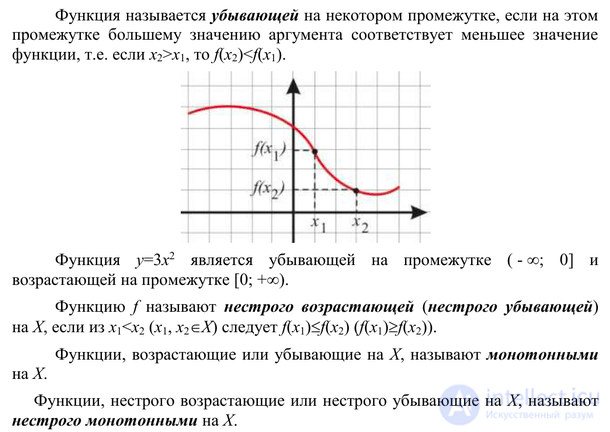
Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) < f(x1).
Пусть дан график функции y = f(x)
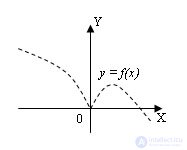
Тогда:
1 . График функции y = f(–x) получается симметричным отображением графика y = f(x) относительно оси OY:
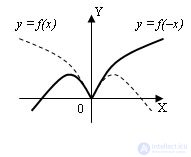
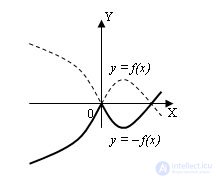
2 . График функции y = –f(x) получается симметричным отображением графика y = f(x) относительно оси OX:
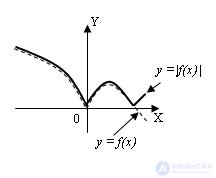
3 . График функции y = |f(x)| получается следующим образом: обводим ту часть графика функции y = f(x), которая лежит выше оси OX, а часть лежащую ниже отобразить симметрично оси OX:
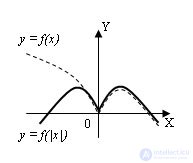
4 . График функции y =f(|x|) получается следующим образом: отбрасываем часть графика функции y = f(x), лежащую левее оси OY, обводим ту часть графика функции y = f(x), которая лежит правее оси OY и отображаем ее симметрично оси OY:
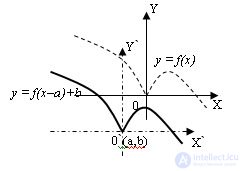
5 .График функции y =f(x–a) + b получается построением графика функции y = f(x) в новой системе координат X`0`Y`, где 0`(a, b), 0`X` || 0X, 0`Y` || 0Y:
6 . График функции y =f(m*x), m > 0, получается из данного растяжением в 1/m раз (если m < 0) от оси OY (вдоль оси OX) и сжатием в m раз (m > 1) к оси OY:
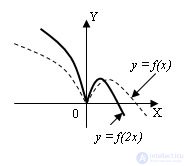
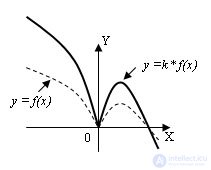
7 . График функции y =k* f(x), k > 0, получается из данного растяжением в k раз (k > 1) относительно оси OX (вдоль оси OY) и сжатием в 1/k раз (при k < 1) к оси OX:
Графики функций важны для наглядного представления и анализа данных. Они используются в:
Для построения графиков функций можно использовать как бумагу и карандаш, так и цифровые инструменты. К наиболее популярным относятся:
График функции помогает визуально понять, как изменяется значение функции при изменении аргумента, а также выявить поведение функции, ее экстремумы и особенности.
Комментарии
Оставить комментарий
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Термины: СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА