Лекция
Привет, сегодня поговорим про дзета-функция римана, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дзета-функция римана , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
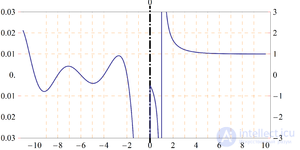
Качественный график дзета-функции Римана на действительной оси. Слева от нуля значения функции увеличены в 100 раз для наглядности
дзета-функция римана — функция 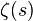 комплексного переменного
комплексного переменного 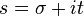 , при
, при 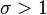 определяемая с помощью ряда Дирихле:
определяемая с помощью ряда Дирихле:
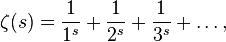
где 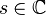 .
.
В заданной области  этот ряд сходится, является аналитической функцией и допускает аналитическое продолжение на всю комплексную плоскость без единицы.
этот ряд сходится, является аналитической функцией и допускает аналитическое продолжение на всю комплексную плоскость без единицы.
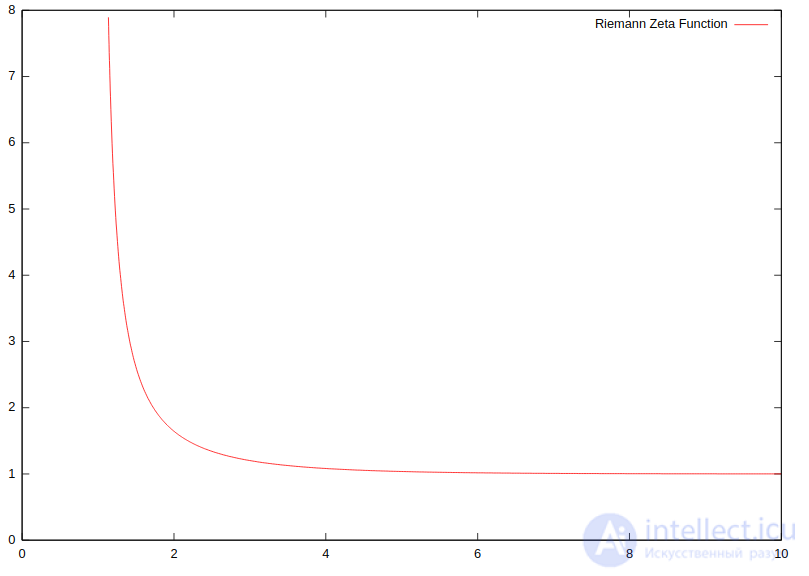
Дзета-функция Римана для вещественных s > 1
В исходной области также верно представление в виде бесконечного произведения (тождество Эйлера)
 ,
,
где произведение берется по всем простым числам 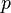 .
.
Почему это так

Решето Эратосфена для поиска простых чисел используется в этом доказательстве.
Идея доказательства использует лишь простую алгебру, доступную прилежному школьнику. Изначально этим способом Эйлер вывел формулу. Есть свойство решета Эратосфена, из которого мы можем извлечь пользу:
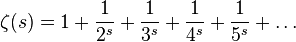
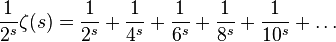
Вычитая второе из первого, мы удаляем все элементы с делителем 2:
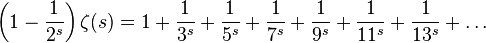
Повторяем для следующего:
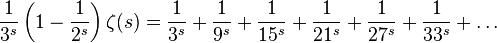
Опять вычитаем, получаем:
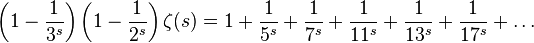
где удалены все элементы с делителями 2 и/или 3.
Как можно увидеть, правая сторона просеивается через решето. Бесконечно повторяя, получаем:

Поделим обе стороны на все, кроме  , получим:
, получим:
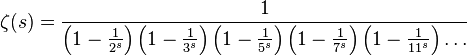
Можно записать короче как бесконечное произведение по всем простым p:

Чтобы сделать доказательство строгим, необходимо потребовать только лишь, чтобы, когда 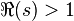 , просеиваемая правая часть приближалась к 1, что немедленно следует из сходимости ряда Дирихле для
, просеиваемая правая часть приближалась к 1, что немедленно следует из сходимости ряда Дирихле для  .
.
Это равенство представляет собой одно из основных свойств дзета-функции.
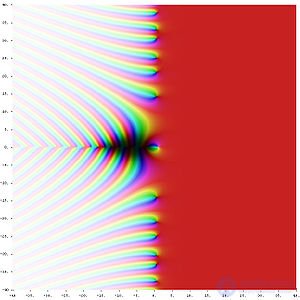
Дзета-функции Римана в комплексной плоскости
 , где
, где 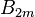 — число Бернулли.
— число Бернулли.
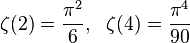 .
.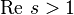
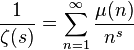 , где
, где 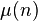 — функция Мебиуса
— функция Мебиуса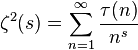 , где
, где 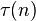 — число делителей числа
— число делителей числа 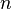
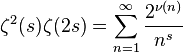 , где
, где 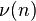 — число простых делителей числа
— число простых делителей числа 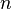
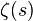 имеет в точке
имеет в точке 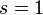 простой полюс с вычетом, равным 1.
простой полюс с вычетом, равным 1.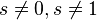 удовлетворяет уравнению:
удовлетворяет уравнению:
 ,
,
где 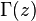 — гамма-функция Эйлера. Это уравнение называется функциональным уравнением Римана.
— гамма-функция Эйлера. Это уравнение называется функциональным уравнением Римана.
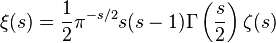 ,
,
введенной Риманом для исследования 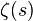 и называемой кси-функцией Римана, это уравнение принимает вид:
и называемой кси-функцией Римана, это уравнение принимает вид:
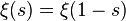 .
.
Как следует из функционального уравнения Римана, в полуплоскости 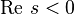 , функция
, функция  имеет лишь простые нули в отрицательных четных точках:
имеет лишь простые нули в отрицательных четных точках: 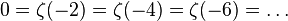 . Эти нули называются «тривиальными» нулями дзета-функции. Далее,
. Эти нули называются «тривиальными» нулями дзета-функции. Далее, 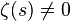 при вещественных
при вещественных 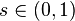 . Следовательно, все «нетривиальные» нули дзета-функции являются комплексными числами. Кроме того, они обладают свойством симметрии относительно вещественной оси и относительно вертикали
. Следовательно, все «нетривиальные» нули дзета-функции являются комплексными числами. Кроме того, они обладают свойством симметрии относительно вещественной оси и относительно вертикали 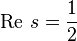 и лежат в полосе
и лежат в полосе 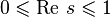 , которая называется критической полосой. Согласно гипотезе Римана, они все находятся на критической прямой
, которая называется критической полосой. Согласно гипотезе Римана, они все находятся на критической прямой 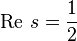 .
.
Существует довольно большое количество специальных функций, связанных с дзета-функцией Римана, которые объединяются общим названием дзета-функции и являются ее обобщениями. Например:
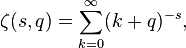
которая совпадает с дзета-функцией Римана при q = 1 (так как суммирование ведется от 0, а не от 1).

который совпадает с дзета-функцией Римана при z = 1.
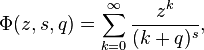
которая совпадает с дзета-функцией Римана при z = 1 и q = 1 (так как суммирование ведется от 0, а не от 1).
В теории гауссовых интегралов по траекториям возникает задача регуляризации детерминантов. Одним из подходов к ее решению является введение дзета-функции оператора. Пусть  — неотрицательно определенный самосопряженный оператор, имеющий чисто дискретный спектр
— неотрицательно определенный самосопряженный оператор, имеющий чисто дискретный спектр 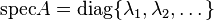 . Причем существует вещественное число
. Причем существует вещественное число 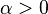 такое, что оператор
такое, что оператор 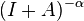 имеет след. Тогда дзета-функция
имеет след. Тогда дзета-функция 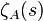 оператора
оператора  определяется для произвольногокомплексного числа
определяется для произвольногокомплексного числа  , лежащего в полуплоскости
, лежащего в полуплоскости 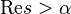 , может быть задана сходящимся рядом
, может быть задана сходящимся рядом
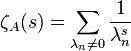
Если заданная таким образом функция допускает продолжение аналитическое продолжение на область, содержащую некоторую окрестность точки  , то на ее основе можно определить регуляризованный детерминант оператора
, то на ее основе можно определить регуляризованный детерминант оператора  в соответствии с формулой
в соответствии с формулой
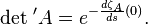
Как функция вещественной переменной, дзета-функция была введена в 1737 году Эйлером, который и указал ее разложение в произведение. Затем эта функция рассматривалась Дирихле и, особенно успешно, Чебышевым при изучении закона распределения простых чисел. Однако наиболее глубокие свойства дзета-функции были обнаружены позднее, после работы Римана (1859), где дзета-функция рассматривалась как функция комплексной переменной.
Вы ведь помните, что такое «простые числа»? Эти числа не делятся ни на какие другие, кроме самих себя и 1. А теперь я задам вопрос, которому уже 3000 лет:
Придумайте суждение или формулу, которые (хотя бы с грехом пополам) прогнозируют, каким будет следующее простое число, (в любом заданном ряду чисел), и ваше имя навечно будет связано с одним из величайших достижений человеческого мозга. Вы встанете в один ряд с Ньютоном, Эйнштейном и Геделем. Разберитесь в поведении простых чисел, и можете потом всю жизнь почивать на лаврах.
Введение
Свойства простых чисел изучались многими великими людьми в истории математики. С первого доказательства бесконечности простых чисел Евклида до формулы произведения Эйлера, связавшей простые числа с дзета-функцией. От формулировки теоремы о простых числах Гаусса и Лежандра до ее доказательства, придуманного Адамаром и Валле-Пуссеном. Тем не менее, Бернхард Риман до сих пор считается математиком, сделавшим единственное крупнейшее открытие в теории простых чисел. В его опубликованной в 1859 году статье, состоявшей всего из восьми страниц, были сделаны новые, ранее неизвестные открытия о распределении простых чисел. Эта статья по сей день считается одной из самых важных в теории чисел.
После публикации статья Римана оставалась главным трудом в теории простых чисел и на самом деле стала основной причиной доказательства в 1896 году теоремы о распределении простых чисел. С тех пор было найдено несколько новых доказательств, в том числе элементарные доказательства Сельберга и Эрдеша. Однако до сих пор остается загадкой гипотеза Римана о корнях дзета-функции.
Сколько всего простых чисел?
Давайте начнем с простого. Все мы знаем, что число является или простым, или составным. Все составные числа состоят из простых и могут быть разложены на их произведения (a x b). В этом смысле простые числа являются «строительными блоками» или «фундаментальными элементами» чисел. В 300 году до нашей эры Евклид доказал, что их количество бесконечно. Его изящное доказательство имеет следующий вид:
Теорема Евклида
Предположим, что множество простых чисел не бесконечно. Создадим список всех простых чисел. Тогда P пусть будет произведением всех простых чисел списка (перемножим все простые числа из списка). Прибавим к результату 1: Q = P +1. Как и все числа, это натуральное число Q должно быть или простым, или составным:
- Если Q простое, то мы нашли простое число, которого нет в нашем «списке всех простых чисел».
- Если Q не простое, то оно составное, т.е. составлено из простых чисел, одно из которых, p, будет делителем Q (потому что все составные числа являются произведениями простых). Каждое простое p, из которого составлено P, очевидно является делителем P. Если p является делителем и для P, и для Q, то оно должно быть и делителем для их разности, то есть единицы. Ни одно простое число не является делителем 1, поэтому число p не может находиться в списке — еще одно противоречие тому, что список содержит все простые числа. Всегда будет существовать еще одно простое p, не находящееся в списке и являющееся делителем Q. Следовательно, простых чисел бесконечно много.
Почему простые числа так сложно понять?
Сам факт того, что любой новичок понимает изложенную выше задачу, красноречиво говорит о ее сложности. Даже арифметические свойства простых чисел, несмотря на активное изучение, плохо нами понимаются. Научное сообщество настолько уверено в нашей неспособности понимать поведение простых чисел, что разложение на множители больших чисел (определение двух простых чисел, произведением которых является число) остается одной из фундаментальных основ теории шифрования. На это можно смотреть следующим образом:
Мы хорошо понимаем составные числа. Это все числа, не являющиеся простыми. Они состоят из простых чисел, но мы можем с легкостью написать формулу, прогнозирующую и/или генерирующую составные числа. Об этом говорит сайт https://intellect.icu . Такой «фильтр составных чисел» называется решетом. Самым знаменитым примером является так называемое «решето Эратосфена», придуманное примерно в 200 году до нашей эры. Его работа заключается в том, что оно просто помечает значения, кратные каждому простому числу вплоть до заданной границы. Допустим, возьмем простое число 2, и пометим 4,6,8,10, и так далее. Затем возьмем 3, и пометим 6,9,12,15, и так далее. В результате у нас останутся только простые числа. Хоть его очень легко понять, решето Эратосфена, как вы можете представить, не особо эффективно.
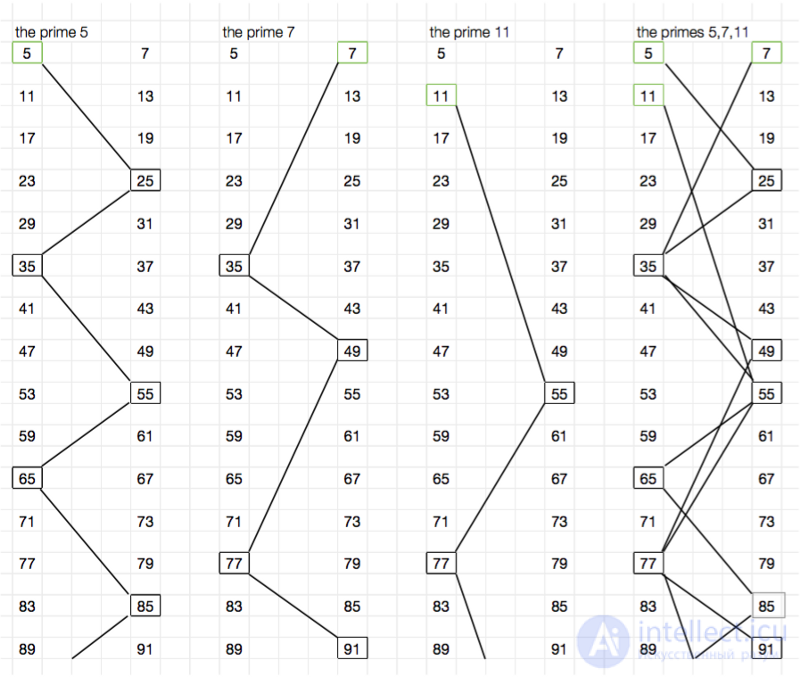
Одной из функций, серьезно упрощающих нашу работу, будет 6n ± 1. Эта простая функция выдает все простые числа, за исключением 2 и 3, и удаляет все числа, кратные 3, а также все четные числа. Подставим n = 1,2,3,4,5,6,7 и получим следующие результаты: 5,7,11,13,17,19,23,25,29,31,35,37,41,43. Единственными не простыми числами, сгенерированными функцией, являются 25 и 35, которые можно разложить на множители 5 x 5 и 5 x 7. Следующими не простыми числами, как вы могли догадаться, будут, 49 = 7 x 7, 55 = 5 x 11, и так далее. Все легко, правда?
Для визуального отображения этого я использовал то, что называю «лестницей составных чисел» — удобный способ показать, как расположены и сочетаются сгенерированные функцией составные числа. В первых трех столбцах показанного ниже изображения мы видим, как красиво поднимаются по каждой лестнице составных чисел простые числа 5, 7 и 11, вплоть до значения 91. Хаос, возникающий в четвертом столбце, показывающем, как решето убрало все, кроме простых чисел — отличная иллюстрация того, почему простые числа так сложно понять.
Как же это все связано с понятием, о котором вы могли слышать — с «гипотезой Римана»? Ну если говорить просто, то чтобы больше понять о простых числах, математики в 19-м веке перестали пытаться спрогнозировать местонахождение простых чисел с абсолютной точностью, и вместо этого начали рассматривать феномен простых чисел в целом. Мастером этого аналитического подхода стал Риман, и в рамках такого подхода была создана его знаменитая гипотеза. Однако прежде чем я начну ее объяснять, необходимо познакомиться с некоторыми фундаментальными ресурсами.
Гармонические ряды
Гармонические ряды — это бесконечные ряды чисел, которые впервые исследовал в 14-м веке Николай Орем. Его имя связано с концепцией музыкальных гармоник — обертонов, которые выше частоты основного тона. Ряды имеют следующий вид:
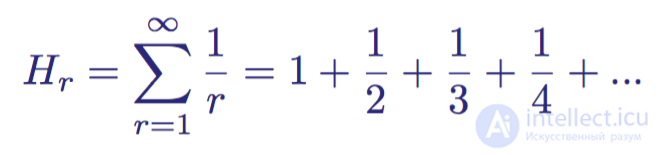
Первые члены бесконечного гармонического ряда
Орем доказал, что эта сумма является несходящейся (то есть не имеющей конечного предела; она не приближается и не стремится к какому-то определенному числу, а устремлена в бесконечность).
Дзета-функции
Гармонические ряды являются особым случаем более общего типа функций под названием дзета-функция ζ(s). Вещественная дзета-функция задается для двух вещественных чисел r и n:
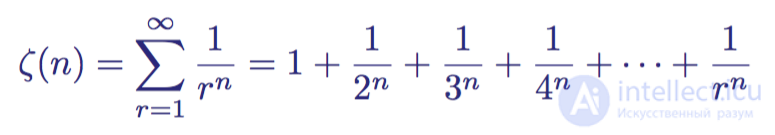
Дзета-функция
Если подставить n = 1, то мы получим гармонический ряд, который расходится. Однако при всех значениях n > 1 ряд сходится, то есть сумма при увеличении r стремится к некому числу, а не уходит в бесконечность.
Формула произведения Эйлера
Первая связь между дзета-функциями и простыми числами была установлена Эйлером, когда он показал, что для двух натуральных (целочисленных и больше нуля) чисел n и p, где p является простым, справедливо следующее:
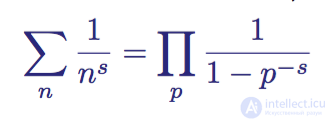
Произведение Эйлера для двух чисел n и p, где оба больше нуля, а p является простым.
Это выражение впервые появилось в статье 1737 года под названием Variae observationes circa series infinitas. Из выражения следует, что сумма дзета-функции равна произведению величин, обратной единице, минус величина, обратная простым числам в степени s. Эта потрясающая связь заложила фундамент современной теории простых чисел, в которой с тех пор дзета-функция ζ(s) начала использоваться как способ изучения простых чисел.
Доказательство формулы — это одно из самых любимых моих доказательств, поэтому я изложу его, хоть для наших целей это и не обязательно (но настолько же оно прекрасно!):
Доказательство формулы произведения Эйлера
Эйлер начинает с общей дзета-функции
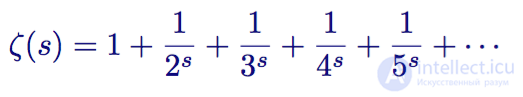
Дзета-функция
Сначала он умножает обе части на второй член:
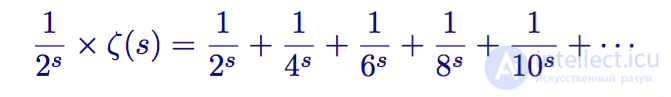
Дзета-функция, умноженная на 1/2s
Затем он вычитает получившееся выражение из дзета-функции:
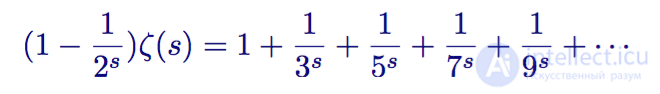
Дзета-функция минус 1/2s, умноженное на дзета-функцию
Он повторяет этот процесс, далее умножая обе стороны на третий член
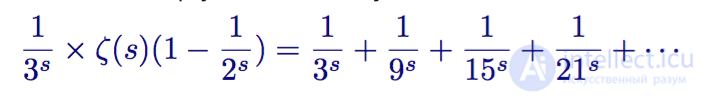
Дзета-функция минус 1/2s, умноженное на дзета-функцию, умноженное на 1/3s
А затем вычитает получившееся выражение из дзета-функции
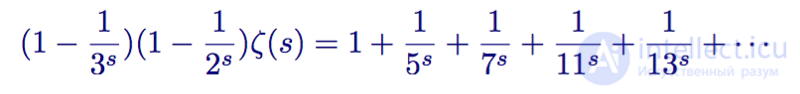
Дзета-функция минус 1/2s, умноженное на дзета-функцию минус 1/3s, умноженное на дзета-функцию
Если повторять этот процесс до бесконечности, в конце концов у нас останется выражение:

1 минус все величины, обратные простым числам, умноженное на дзета-функцию
Если этот процесс вам знаком, то это потому, что Эйлер по сути создал решето, очень похожее на решето Эратосфена. Он отфильтровывает из дзета-функции числа, не являющиеся простыми.
Затем разделим выражение на все его члены, являющимися обратными простым числам величинами, и получим:
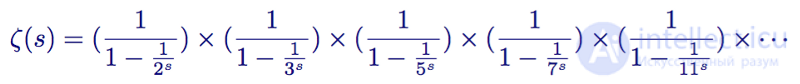
Функциональная связь дзета-функции с простыми числами для первых простых чисел 2,3,5,7 и 11
Упростив выражение, мы показали следующее:
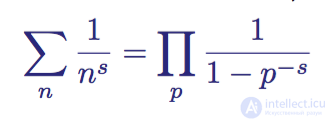
Формула произведения Эйлера — равенство, показывающее связь между простыми числами и дзета-функцией
Разве это было не красиво? Подставим s = 1, и найдем бесконечный гармонический ряд, повторно доказав бесконечность простых чисел.
Функция Мебиуса
Август Фердинанд Мебиус переписал произведение Эйлера, создав новую сумму. Кроме величин, обратных простым числам, функция Мебиуса также содержит каждое натуральное число, являющееся произведением четного и нечетного количества простых множителей. Числа, исключенные из его ряда — это такие числа, которые делятся на какое-то простое число в квадрате. Его сумма, обозначаемая как μ(n), имеет следующий вид:
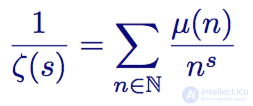
Функция Мебиуса — измененная версия произведения Эйлера, заданная для всех натуральных чисел
Сумма содержит величины, обратные:
Ниже показаны первые члены:
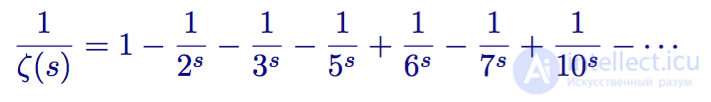
Ряд/сумма единиц, разделенных на дзета-функцию ζ(s)
Сумма не содержит те обратные величины, которые делятся на квадрат одного из простых чисел, например, 4,8,9, и так далее.
Функция Мебиуса μ(n) может принимать только три возможных значения: префикс (1 или -1) или удаление (0) членов из суммы:

Три возможных значения функции Мебиуса μ(n)
Хотя впервые эта хитрая сумма была формально определена Мебиусом, примечательно, что за 30 лет до него об этой сумме писал в заметках на полях Гаусс:
«Сумма всех первообразных корней (простого числа p) или ≡ 0 (когда p-1 делится на квадрат), или ≡ ±1 (mod p) (когда p-1 является произведением неравных простых чисел); если их количество четно, то знак положителен, но если количество нечетно, то знак отрицателен».
Функция распределения простых чисел
Вернемся к простым числам. Чтобы понять, как распределяются простые числа при движении вверх по числовой прямой, не зная точно, где они находятся, полезно будет подсчитать, сколько их встречается до определенного числа.
Именно эту задачу выполняет предложенная Гауссом функция распределения простых чисел π(x): она дает нам количество простых чисел, меньших или равных заданному вещественному числу. Поскольку мы не знаем формул для нахождения простых чисел, формула распределения простых чисел известна нам только как график, или ступенчатая функция, увеличивающаяся на 1, когда x является простым числом. На графике ниже показана функция до x = 200.
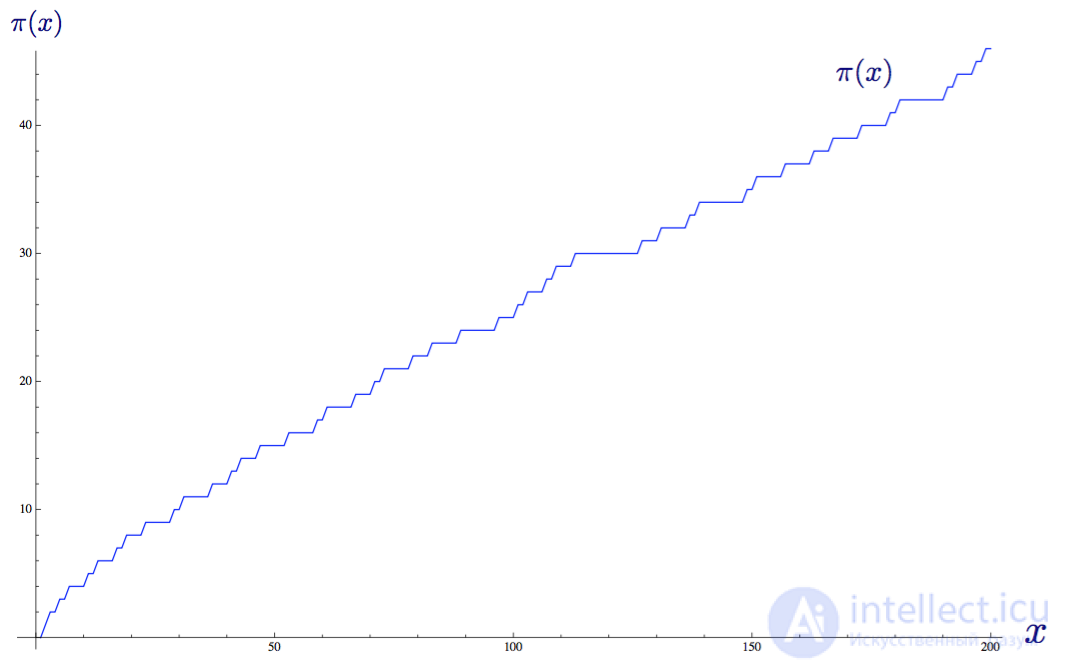
Функция распределения простых чисел π(x) до значения x = 200.
Теорема о распределении простых чисел
Теорема о распределении простых чисел, сформулированная Гауссом (и независимо от него Лежандром), гласит:
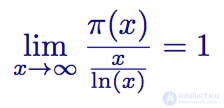
Теорема о распределении простых чисел
Обычным языком это можно изложить так: «При движении x к бесконечности функция распределения простых чисел π(x) будет приближаться к функции x/ln(x)». Другими словами, если забраться достаточно далеко, и график распределения простых чисел поднимется до очень высокого числа x, то при делении x на натуральный логарифм x соотношение этих двух функций будет стремиться к 1. Ниже на графике показаны две функции для x = 1000:
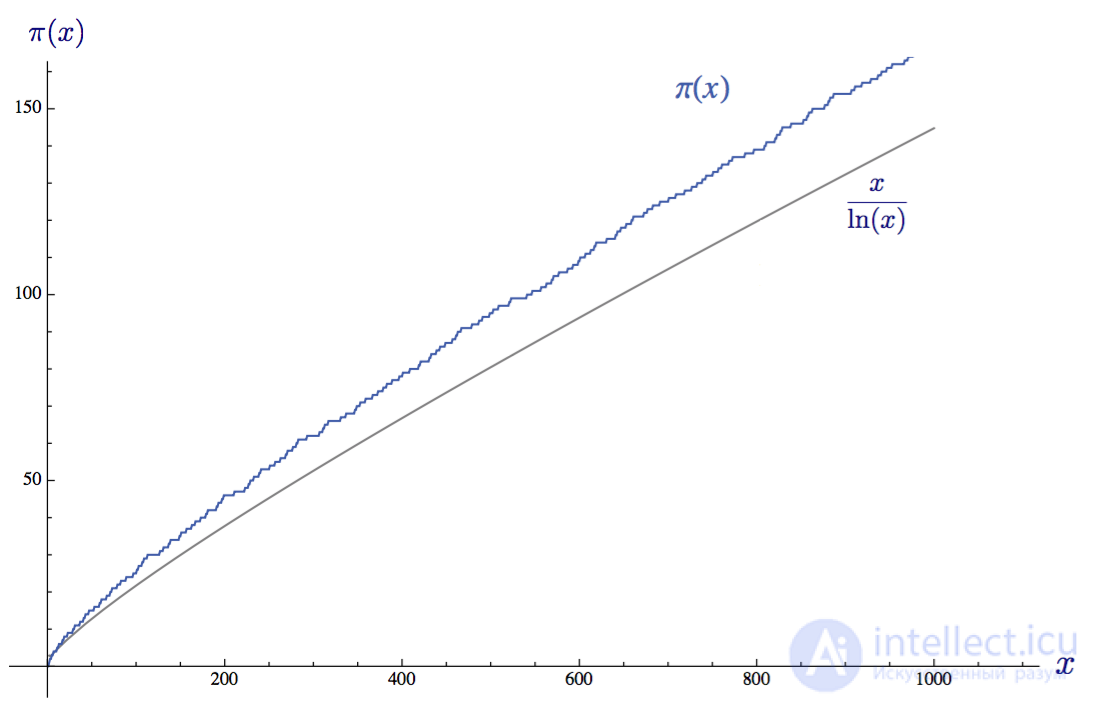
Функция распределения простых чисел π(x) и приблизительная оценка по теореме распределения простых чисел до x = 1000
С точки зрения вероятностей, теорема о распределении простых чисел гласит, что если случайным образом выбрать натуральное число x, то вероятность P(x) того, что это число будет простым, примерно равно 1 / ln(x). Это означает, что средний разрыв между последовательными простыми числами среди первых x целочисленных значений приблизительно равен ln(x).
Интегральный логарифм
Функция Li(x) определена для всех положительных вещественных чисел, за исключением x = 1. Она задается интегралом от 2 до x:
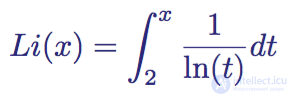
Интегральное представление функции интегрального логарифма
Построив график этой функции рядом с функцией распределения простых чисел и формулой из теоремы о распределении простых чисел, мы видим, что Li(x) на самом деле является лучшим приближением, чем x/ln(x):
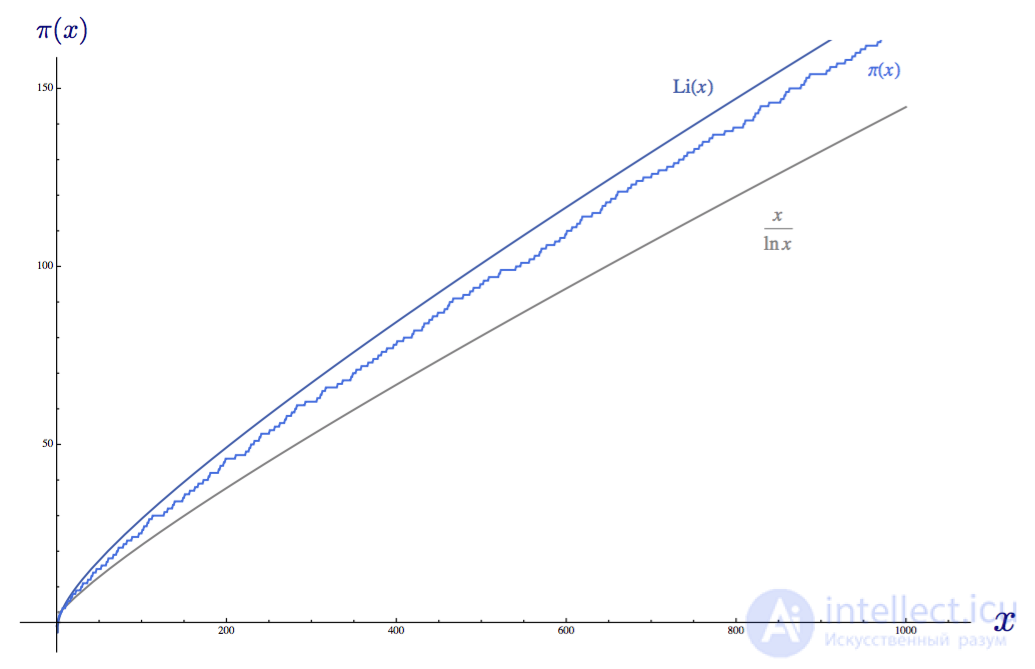
Интегральный логарифм Li(x), функция рапределения простых чисел π(x) и x/ln(x) на одном графике
Чтобы узнать, насколько лучше это приближение, мы можем построить таблицу с большими значениями x, количеством простых чисел до x и величиной погрешности между старой (теорема о распределении простых чисел) и новой (интегральный логарифм) функциями:
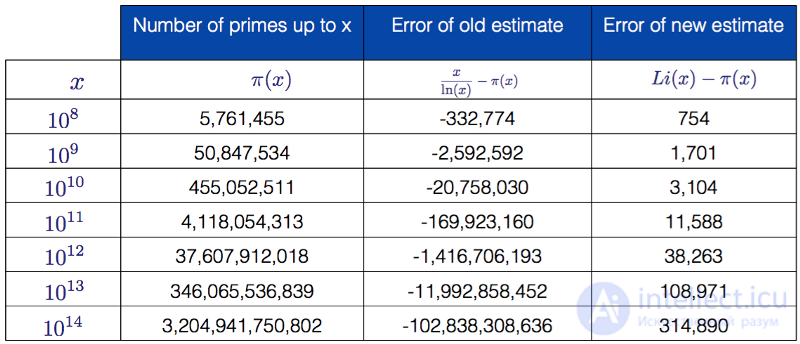
Количество простых чисел до заданной степени десятки и соответствующие погрешности для двух приближений
Как легко можно заметить, интегральный логарифм намного лучше в приближении, чем функция из теоремы о распределении простых чисел, он «ошибся» в большую сторону всего на 314 890 простых чисел для x = 10 в степени 14. Тем не менее, обе функции сходятся к функции распределения простых чисел π(x). Li(x) сходится гораздо быстрее, но при стремлении x к бесконечности соотношение между функцией распределения простых чисел и функциями Li(x) и x/ln(x) приближается к 1. Покажем это наглядно:
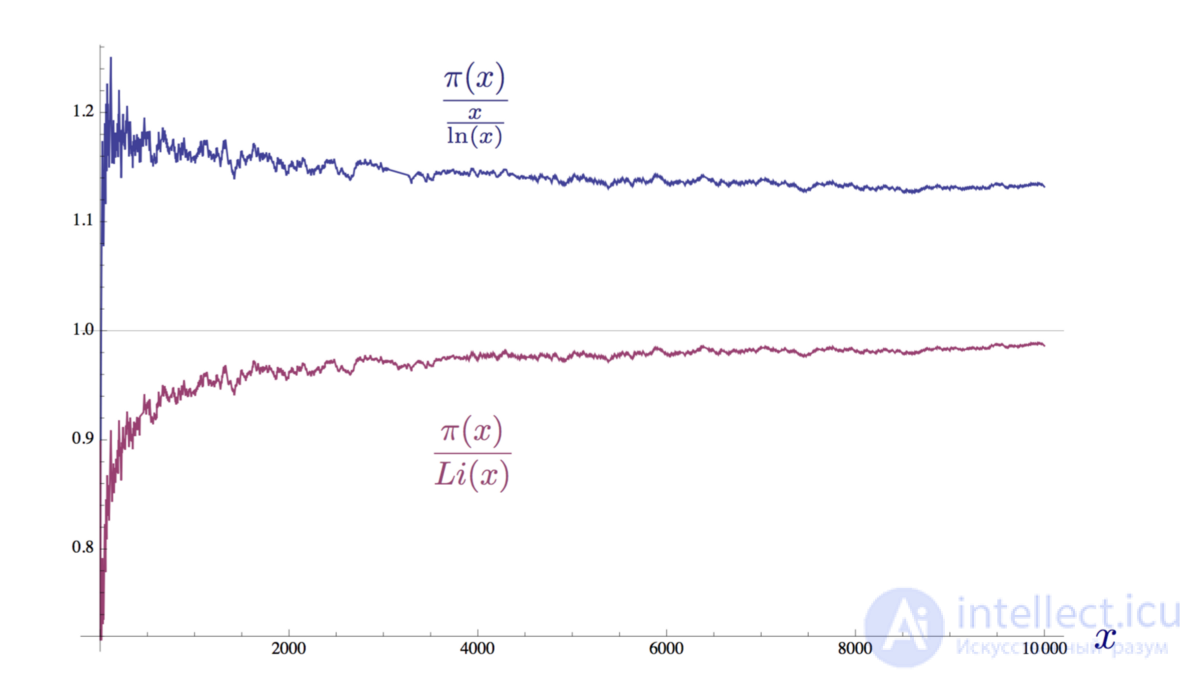
Схождение соотношений двух приближенных значений и функции распределения простых чисел к 1 при x = 10 000
Гамма-функция
Гамма-функция Γ(z) стала важным объектом для изучения с тех пор, когда в 1720-х годах Даниил Бернулли и Христиан Гольдбах исследовали задачу обобщения функции факториала на нецелые аргументы. Это обобщение функции факториала n! (1 x 2 x 3 x 4 x 5 x …. n), сдвинутое вниз на 1:

Гамма-функция, определенная для z
Ее график очень любопытен:
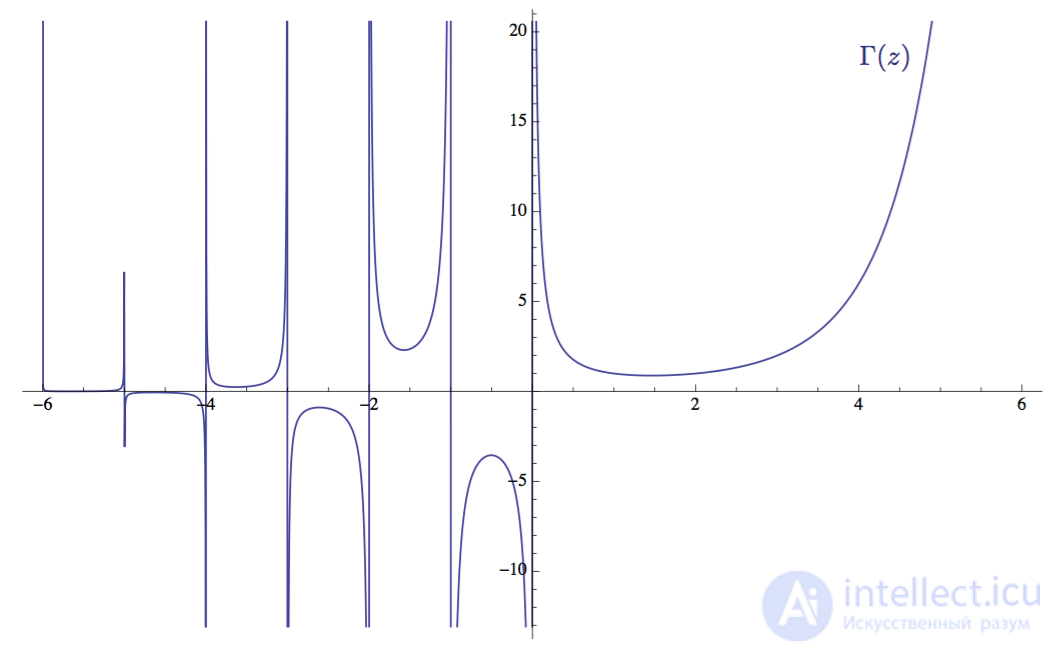
График гамма-функции Γ(z) в интервале -6 ≤ z ≤ 6
Гамма-функция Γ(z) определена для всех комплексных значений z больше нуля. Как вы наверно знаете, комплексные числа — это класс чисел с мнимой частью, записываемых как Re(z) + Im(z), где Re(z) — это вещественная часть (обычное вещественное число), а Im(z) — мнимая часть, обозначаемая буквой i. Комплексное число обычно записывается в виде z = σ + it, где сигма σ — вещественная часть, а it — мнимая. Комплексные числа полезны тем, что они позволяют математикам и инженерам работать с задачами, недоступными обычным вещественным числам. В графическом виде комплексные числа расширяют традиционную одномерную числовую прямую в двухмерную числовую плоскость, называемую комплексной плоскостью, в которой вещественная часть комплексного числа откладывается по оси x, а мнимая — по оси y.
Чтобы гамма-функцию Γ(z) можно было использовать, ее обычно переписывают в виде
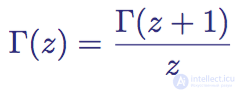
Функциональная связь гамма-функции Γ(z)
С помощью этого равенства мы можем получить значения для z ниже нуля. Однако оно не дает значений для отрицательных целых чисел, потому что они не определены (формально они являются вырожденностями или простыми полюсами).
Дзета и гамма
Связь между дзета-функцией и гамма-функцией задается следующим интегралом:
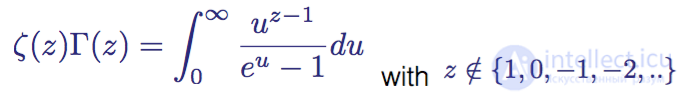
Ознакомившись со всеми необходимыми фундаментальными ресурсами, мы можем наконец приступать к установлению связи между простыми числами и гипотезой Римана.
Немецкий математик Бернхард Риман родился в 1826 году в Брезеленце. Будучи студентом Гаусса, Риман опубликовал работу в области математического анализа и геометрии. Считается, что наибольший вклад он внес в области дифференциальной геометрии, где заложил фундамент языка геометрии, позже использованного Эйнштейном в общей теории относительности.

Его единственный труд в теории чисел, статья 1859 года Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse («О простых числах меньше заданной величины») считается самой важной статьей в этой области математики. Всего на четырех страницах он изложил:
Это невероятный пример изобретательности и творческого мышления, подобных которому, вероятно, с тех пор не встречалось. Совершенно потрясающий труд.
Мы видели тесную связь между простыми числами и дзета-функцией, показанную Эйлером в его произведении. Однако за исключением этой связи об их взаимоотношениях было мало что известно, и чтобы показать их, потребовалось изобретение комплексных чисел.
Риман первым рассмотрел дзета-функцию ζ(s) для комплексной переменной s, где s = σ + it.
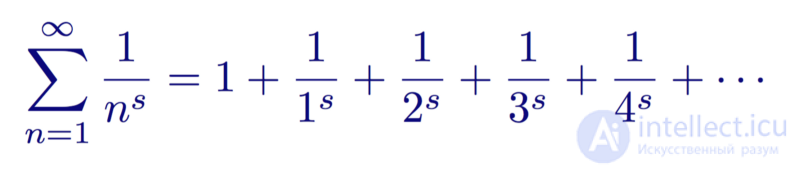
Дзета-функция Римана для n, где s = σ + it — это комплексное число, в котором σ и t являются вещественными числами.
Этот бесконечный ряд, названный дзетой-функцией Римана ζ(s), является аналитическим (то есть имеет определяемые значения) для всех комплексных чисел с вещественной частью больше 1 (Re(s) > 1). В этой области определения он сходится абсолютно.
Чтобы проанализировать функцию в областях за пределами обычной области сходимости (когда вещественная часть комплексной переменной s больше 1), функцию нужно переопределить. Риман успешно с этим справился, выполнив аналитическое продолжение до абсолютно сходящейся функции на полуплоскости Re(s) > 0.
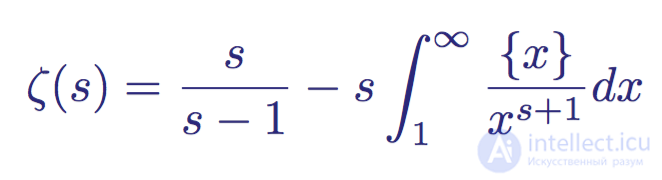
Переписанный вид дзета-функции Римана, где {x} = x — |x|
Это новое определение дзета-функции аналитично в любой части полуплоскости Re(s) > 0, за исключением s = 1, где она является вырожденностью/простым полюсом. В этой области определения она называется мероморфной функцией, потому что она голоморфна (комплексно дифференцируема в окрестности каждой точки в области ее определения), за исключением простого полюса s = 1. Кроме того, она является превосходным примером L-функции Дирихле.
В своей статье Риман на этом не остановился. Он перешел к аналитическому продолжению своей дзета-функции ζ(s) на всю комплексную плоскость, воспользовавшись гамма-функцией Γ(z). Чтобы не усложнять пост, я не буду приводить эти вычисления, но крайне рекомендую вам посмотреть их самостоятельно, чтобы убедиться в удивительной интуиции и мастерстве Римана.
В его методе используется интегральное представление гаммы Γ(z) для комплексных переменных и тета-функции Якоби ϑ(x), которые можно переписать таким образом, чтобы появилась дзета-функция. Решая относительно дзета, получаем:

Функциональное уравнение дзеты для всей комплексной плоскости за исключением двух вырожденностей при s = 0 и s = 1
В таком виде мы замечаем, что член ψ(s) уменьшается быстрее чем любая степень x, а значит, интеграл сходится ко всем значениям s.
Зайдя еще дальше, Риман заметил, что первый член в скобках (-1 / s(1 — s) ) является инвариантом (не меняется), если заменить s на 1 — s. Благодаря этому Риман еще больше расширил полезность уравнения, устранив два полюса в s=0 и s=1, и задав кси-функцию Римана ξ(s) без вырожденностей:
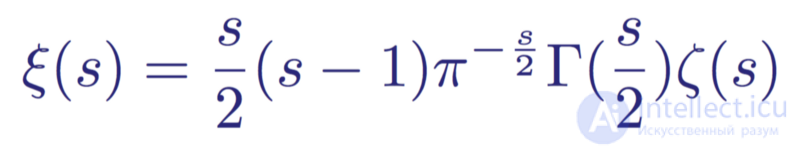
Кси-функция Римана ξ(s)
Корни/нули дзета-функции, когда ζ(s)=0, можно разделить на два вида, которые называются «тривиальными» и «нетривиальными» нулями дзета-функции Римана.
Существование нулей с вещественной частью Re(s) < 0
Тривиальные нули — это нули, которые легко найти и объяснить. Наиболее заметны они в следующем функциональном виде дзета-функции:
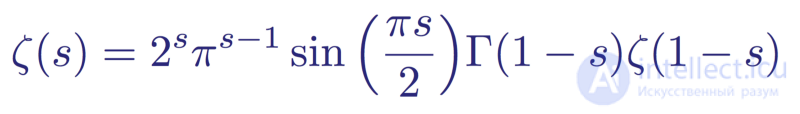
Разновидность функционального дзета-уравнения Римана
Это произведение становится равным нулю, когда нулем становится синус. Это происходит при значениях kπ. То есть при отрицательном четном целом числе s = -2n дзета-функция становится нулем. Однако для положительных четных целых чисел s = 2n нули сокращаются полюсами гамма-функции Γ(z). Это легче увидеть в исходном функциональном виде; если подставить s = 2n, то первая часть члена становится неопределенной.
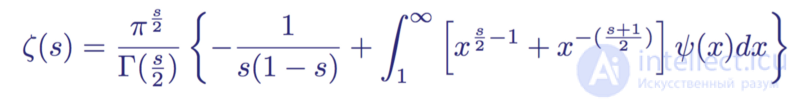
Итак, дзета-функция Римана имеет нули в каждом отрицательном четном целом s = -2n. Это тривиальные нули, и их можно увидеть на графике функции:
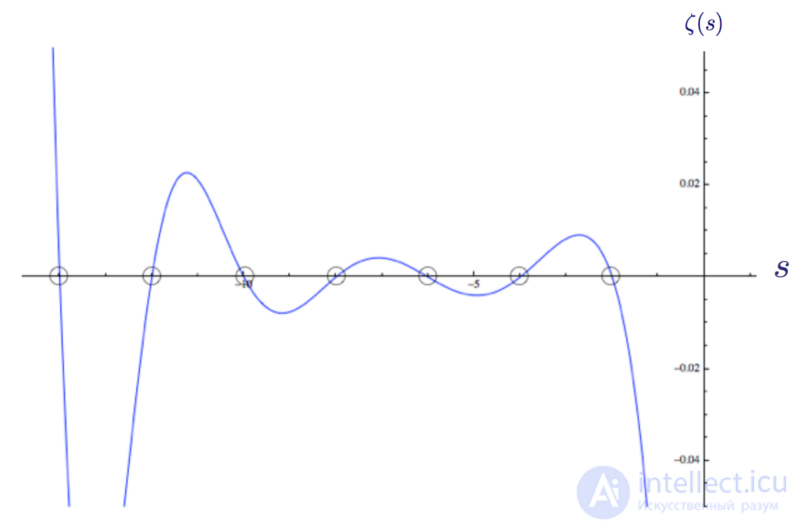
График дзета-функции Римана ζ(s) с нулями в s= -2, -4, -6 и так далее
Существование нулей с вещественной частью Re(s) > 1
Из формулировки дзеты Эйлера мы можем мгновенно увидеть что дзета ζ(s) не может быть нулем в области с вещественной частью s больше 1, потому что сходящееся бесконечное произведение может быть нулем только если равен нулю один из его множителей. Доказательство бесконечности простых чисел отрицает это.
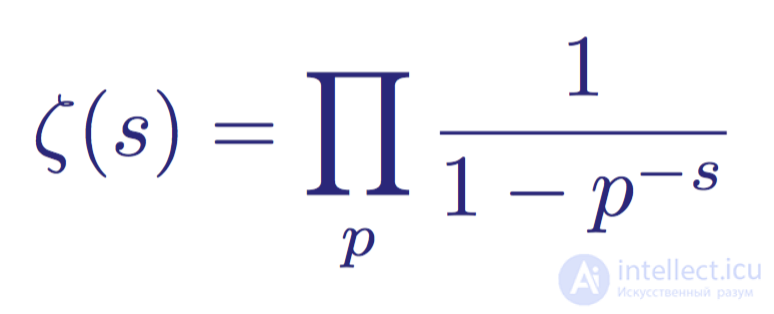
Формула произведения Эйлера
Существование нулей с вещественной частью 0 ≤ Re(s) ≤ 1
Мы нашли тривиальные нули дзеты в отрицательной полуплоскости, когда Re(s) < 0, и показали, что в области Re(s) > 1 не может быть нулей.
Однако область между этими двумя областями, называемая критической полосой, была основным центром внимания аналитической теории чисел в течение последних сотен лет.
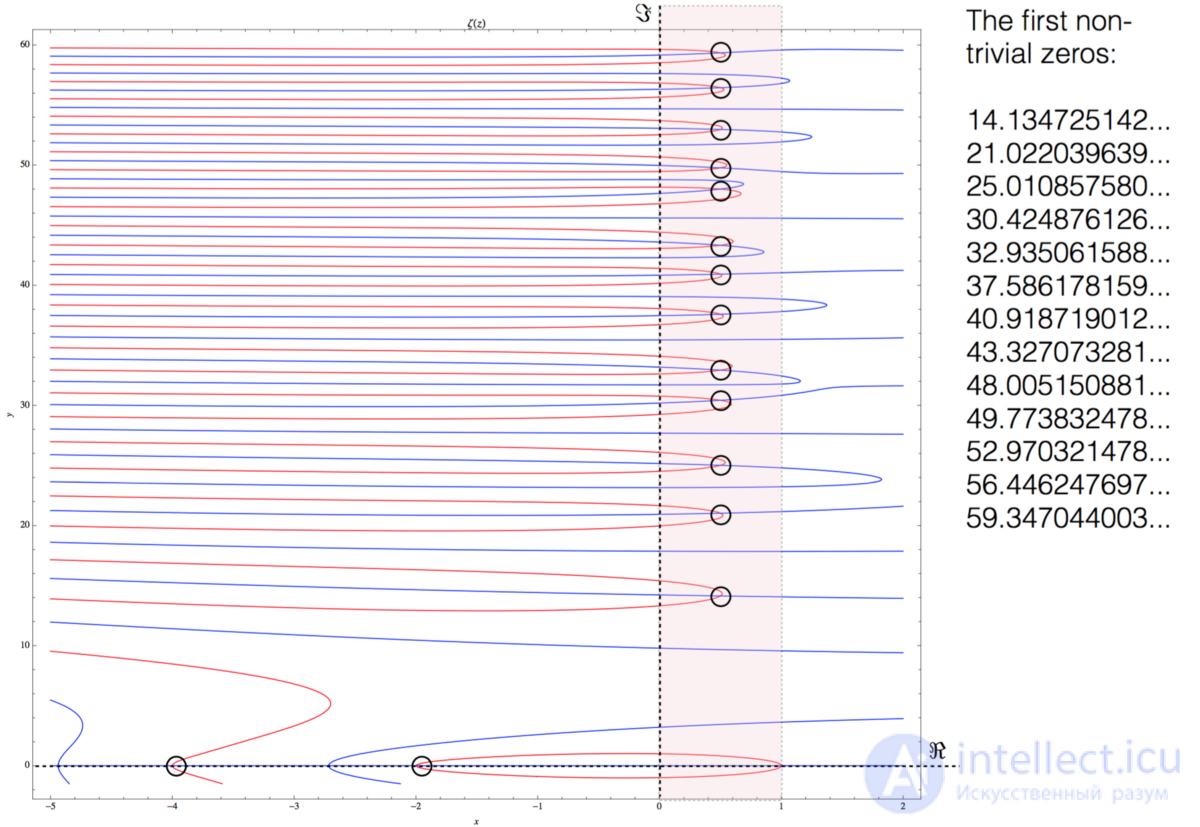
График вещественной и мнимой частей дзета-функции Римана ζ(s) в интервале -5 < Re < 2, 0 < Im < 60
На показанном выше графике я отобразил вещественные части дзеты ζ(s) красным, а мнимые — синим. Мы видим первые два тривиальных нуля в левом нижнем углу, где вещественная часть s равна -2 и -4. Между 0 и 1 я выделил критическую полосу и отметил пересечения вещественных и мнимых частей дзеты ζ(s). Это нетривиальные нули дзета-функции Римана. Поднимаясь к более высоким значениям, мы увидим больше нулей и две кажущиеся случайными функции, которые становятся плотнее при увеличении значений мнимой части s.
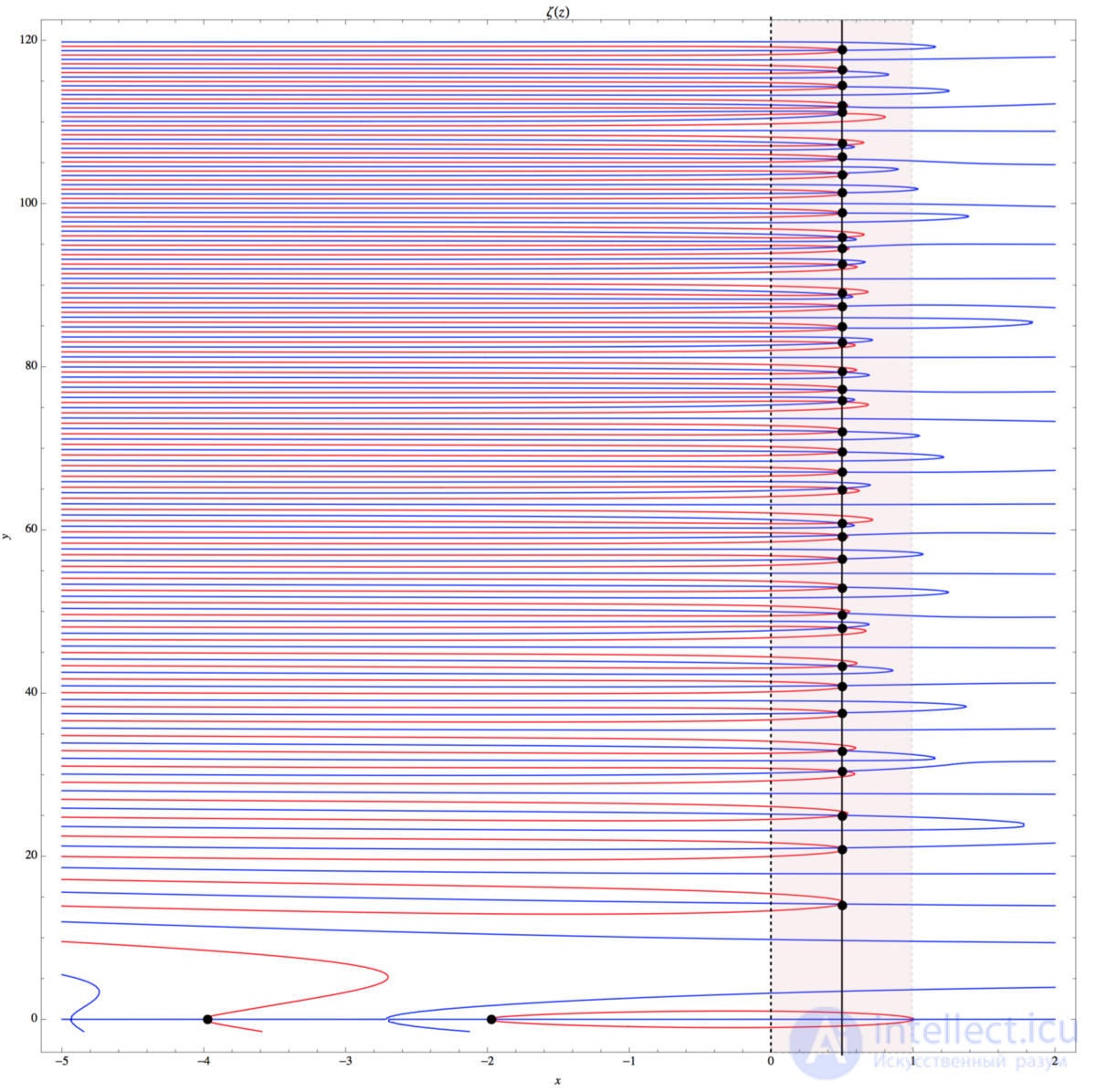
График вещественной и мнимой частей дзета-функции Римана ζ(s) в интервале -5 < Re < 2, 0 < Im < 120
Кси-функция Римана
Мы определили кси-функцию Римана ξ(s) (вид функционального уравнения, в котором устранены все вырожденности, то есть оно определено для всех значений s) так:
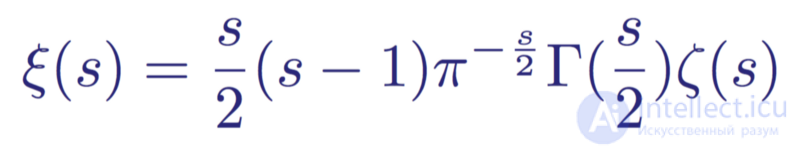
Кси-функция Римана без вырожденностей
Эта функция удовлетворяет соотношению
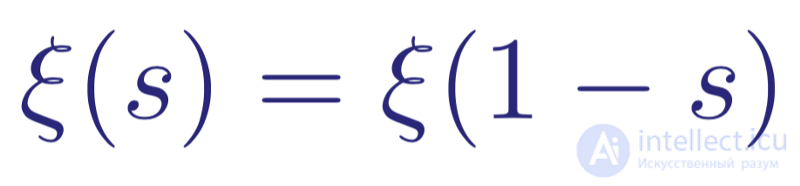
Симметричная взаимосвязь между положительными и отрицательными значениями кси-функции Римана
Это означает, что функция симметрична относительно вертикальной линии Re(s) = 1/2, то есть ξ(1) = ξ(0), ξ(2) = ξ(-1), и так далее. Эта функциональная связь (симметрия s и 1-s) в сочетании с произведением Эйлера показывают, что кси-функция Римана может иметь нули только в интервале 0 ≤ Re(s) ≤ 1. Другими словами, нули кси-функции Римана соответствуют нетривиальным нулям дзета-функции Римана. В известном отношении, критическая линия R(s) = 1/2 для дзета-функции Римана ζ(s) соответствует вещественной линии (Im(s) = 0) для кси-функции Римана ξ(s).
Посмотрев на два показанных выше графика, можно сразу заметить, что у всех нетривиальных нулей дзета-функции Римана ζ(s) (нулей кси-функции Римана) вещественная часть Re(s) равна 1/2. В своей статье Риман вкратце упомянул это свойство, и его поверхностное примечание в результате оказалось одним из величайших его наследий.
У нетривиальных нулей дзета-функции Римана ζ(s) вещественная часть имеет вид Re(s) = 1/2.
Это современная формулировка недоказанного предположения, сделанного Риманом в его знаменитой статье. Она гласит, что все точки, в которых дзета равна нулю (ζ(s) = 0) на критической полосе 0 ≤ Re(s) ≤ 1, имеют вещественную часть Re(s) = 1/2. Если это верно, то все нетривиальные нули дзеты будут иметь вид ζ(1/2 + it).
Эквивалентная формулировка (изложенная самим Риманом) заключается в том, что все корни кси-функции Римана ξ(s) вещественны.
На графике ниже линия Re(s) = 1/2 является горизонтальной осью. Вещественная часть Re(s) дзеты ζ(s) показана красной линией, а мнимая часть Im(s) — синей. Нетривиальные нули — это пересечения между красным и синим графиками на горизонтальной прямой.
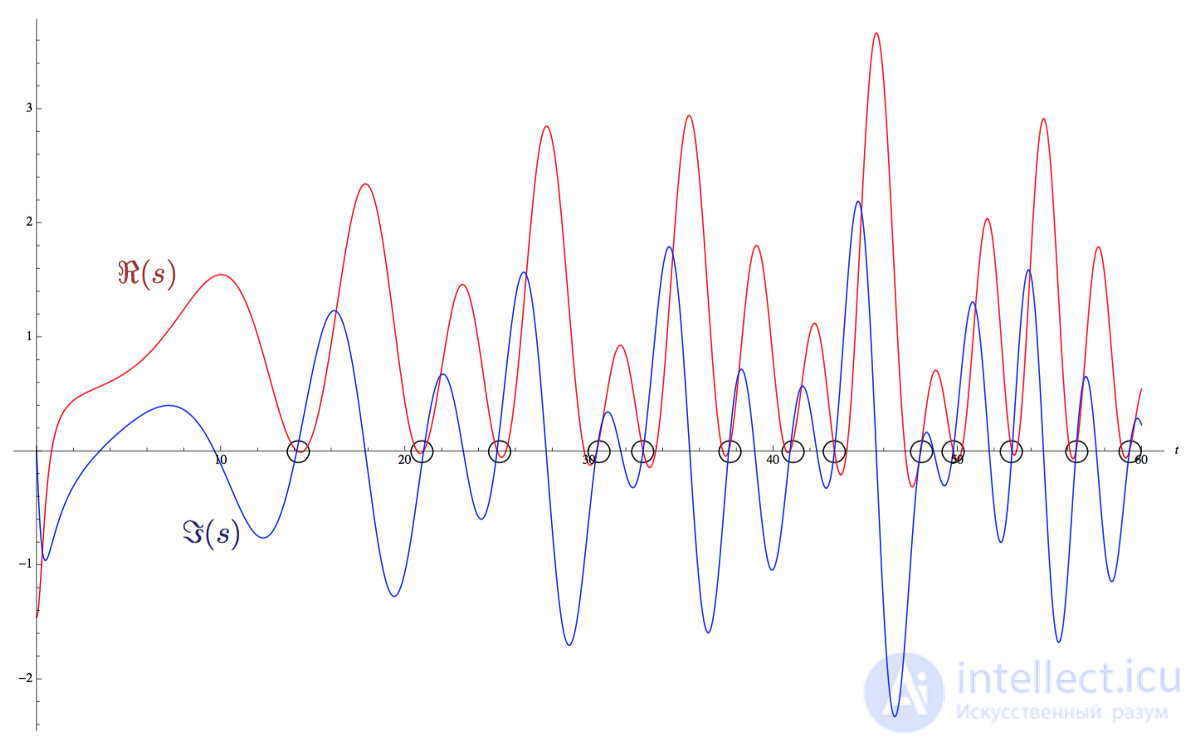
Первые нетривиальные нули дзета-функции Римана на прямой Re(s) = 1/2.
Если гипотеза Римана окажется истинной, то все нетривиальные нули функции будут встречаться на этой прямой как пересечения двух графиков.
Причины верить в гипотезу
Существует множество причин верить истинности гипотезы Римана относительно нулей дзета-функции. Наверно, самым убедительной для математиков причиной являются последствия, которые она будет иметь для распределения простых чисел. Численная проверка гипотезы при очень высоких значениях предполагает, что она истинна. На самом деле, численное подтверждение гипотезы настолько сильно, что в других областях, например, в физике или химии, его можно было бы считать экспериментально доказанным. Однако в истории математики было несколько гипотез, проверенных до очень высоких значений, и тем не менее оказавшихся неверными. Дербишир (2004) рассказывает историю числа Скьюза — чрезвычайно большого числа, указавшего верхний предел и доказавшего таким образом ложность одной из гипотез Гаусса о том, что интегральный логарифм Li(x) всегда больше, чем функция распределения простых чисел. Она была опровергнута Литлвудом без примера, а затем было показано, что она неверна выше очень огромного числа Скьюза — десять в степени десять, в степени десять, в степени 34. Это доказало, что несмотря на доказанность ошибочности идеи Гаусса, пример точного местонахождения такого отклонения от гипотезы находится далеко за пределами даже современных вычислительных мощностей. Такое может произойти и в случае с гипотезой Римана, которая была проверена «всего лишь» до десятки в степени двенадцати нетривиальных нулей.
Взяв за основу истинность гипотезы Римана, сам Риман начал исследовать ее последствия. В своей статье он писал: "…есть большая вероятность того, что все корни являются вещественными. Разумеется, здесь нужно строгое доказательство; сделав несколько безуспешных попыток, я отложу его поиск, потому что оно кажется необязательным для следующей цели моих исследований". Его следующей целью была связь нулей дзета-функции с простыми числами.
Вспомним функцию распределения простых чисел π(x), подсчитывающую количество простых чисел вплоть до вещественного числа x. Риман использовал π(x) для определения собственной функции распределения простых чисел, а именно функции распределения простых чисел Римана J(x). Она задается следующим образом:
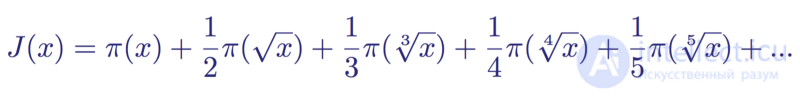
Функция распределения простых чисел Римана
Первое, что можно заметить в этой функции — она не бесконечна. При каком-то члене функция распределения будет равна нулю, потому что не существует простых чисел для x < 2. То есть взяв для примера J(100), мы получим, что функция состоит из семи членов, потому что восьмой член будет содержать восьмой корень 100, который приблизительно равен 1.778279.., то есть этот член распределения простых чисел становится равным нулю, а сумма становится равной J(100) = 28.5333…
Как и функция распределения простых чисел, функция Римана J(x) — это ступенчатая функция, значение которой увеличивается так:

Возможные значения функции распределения простых чисел Римана
Чтобы связать значение J(x) с количеством простых чисел до x, включая его, мы вернемся к функции распределения простых чисел π(x) при помощи процесса, называемого обращением Мебиуса (здесь я его показывать не буду). Полученное выражение будет иметь вид
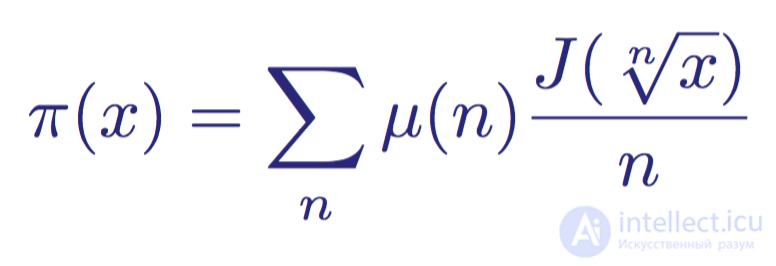
Функция распределения простых чисел π(x) и ее связь с функцией распределения простых чисел Римана и с функцией Мебиуса μ(n)
Вспомним, что возможные значения функции Мебиуса имеют вид

Три возможных значения функции Мебиуса μ(n)
Это значит, что теперь мы можем записать любую функцию распределения простых чисел как функцию распределения простых чисел Римана, что даст нам
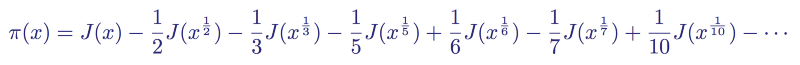
Функция распределения простых чисел, записанная как функция распределения простых чисел Римана для первых семи значений n
Это новое выражение по-прежнему является конечной суммой, потому что J(x) равна нулю при x < 2, так как не существует простых чисел меньше 2.
Если теперь мы еще раз рассмотрим пример с J(100), то получим сумму
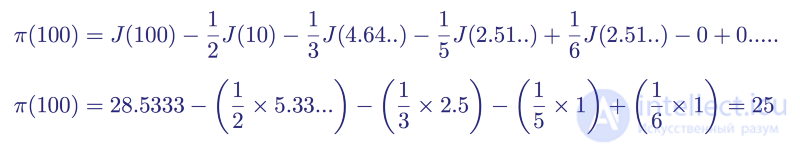
Функция распределения простых чисел для x = 100
Что, как мы знаем, является количеством простых чисел ниже 100.
Преобразование формулы произведения Эйлера
Затем Риман использовал в качестве начальной точки произведение Эйлера и получил метод для аналитической оценки простых чисел на неподдающемся исчислению языке матанализа. Начав с Эйлера:
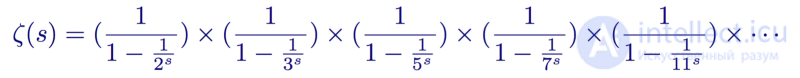
Произведение Эйлера для первых пяти простых чисел
Сначала взяв с обеих сторон логарифм а затем переписав знаменатели в скобках, он вывел взаимоотношение
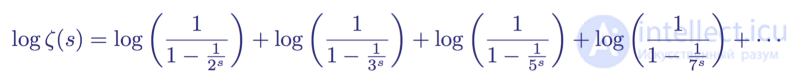
Логарифм переписанной формулы произведения Эйлера
Затем, воспользовавшись хорошо известным рядом Тейлора-Маклорена, он разложил каждый логарифмический член в правой части, создав бесконечную сумму бесконечных сумм, по одной для каждого члена в ряду простых чисел.

Разложение Тейлора для первых четырех членов логарифма произведения Эйлера
Рассмотрим один из таких членов, например:
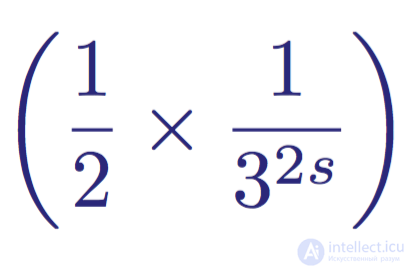
Второй член — это разложение Маклорена для 1/3^s
Этот член, как и каждый другой член вычисления, представляет часть площади под функцией J(x). В виде интеграла:

Интегральный вид второго члена разложения Маклорена для 1/3^s
Другими словами, с помощью произведения Эйлера Риман показал, что можно представить дискретную ступенчатую функцию распределения простых чисел в виде непрерывной суммы интегралов. На графике ниже взятый нами пример члена показан как часть площади под графиком функции распределения простых чисел Римана.
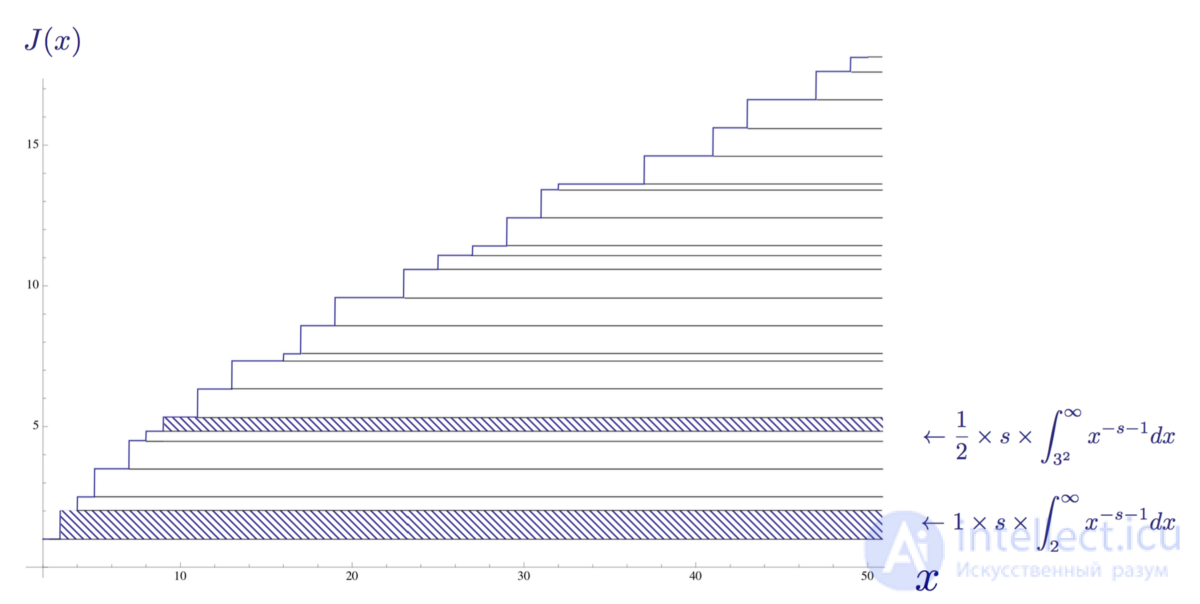
Функция распределения простых чисел Римана J(x) до x = 50, в котором выделены два интеграла
Итак, каждое выражение в конечной сумме, составляющей ряд величин, обратных простым числам из произведения Эйлера, может быть выражена в виде интегралов, составляющих бесконечную сумму интегралов, соответствующих площади под функцией распределения простых чисел Римана. Для простого числа 3 это бесконечное произведение интегралов имеет вид:

Бесконечное произведение интегралов, составляющих площадь под функцией распределения простых чисел, представленной целочисленной 3
Если собрать все эти бесконечные суммы вместе в один интеграл, то интеграл под функцией распределения простых чисел Римана J(x) может быть записан в простом виде:
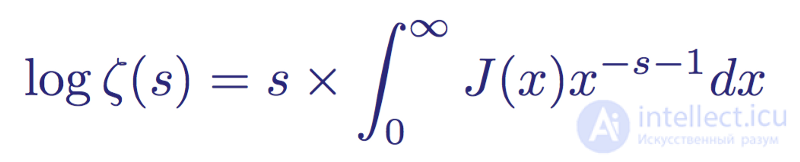
Логарифм дзеты, выраженный в виде бесконечного ряда интегралов
Или в более известном виде

Современный эквивалент произведения Эйлера, связывающий дзета-функцию с функцией распределения простых числе Римана
Благодаря этому Риману удалось связать на языке матанализа свою дзета-функцию ζ(s) с функцией распределения простых чисел Римана J(x) в равенстве, эквивалентном формуле произведения Эйлера.
Величина погрешности
Получив этот аналитический вид произведения Эйлера, Риман приступил к формулированию собственной теоремы о распределении простых чисел. Он представил ее в следующем явном виде:
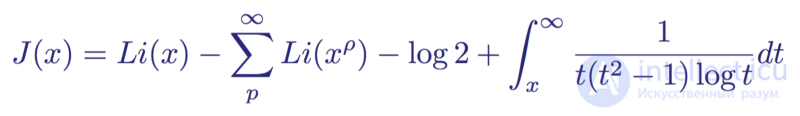
«Теорема о распределении простых чисел Римана», предугадывающая количество простых чисел меньше заданной величины x
Это явная формула Римана. Она стала усовершенствованием теоремы о распределении простых чисел, более точной оценкой количества простых чисел вплоть до числа x. Формула состоит из четырех членов:
Влияние двух последних членов на значение функции с ростом x становится чрезвычайно малым. Основной «вклад» для больших чисел делают функция интегрального логарифма и периодическая сумма. См. их влияние на графике:

Ступенчатая функция распределения простых чисел π(x), аппроксимируемая явной формулой функции распределения простых чисел Римана J(x) с помощью первых 35 нетривиальных нулей ρ дзета-функции Римана.
В показанном выше графике я аппроксимировал функцию распределения простых чисел π(x) с помощью явной формулы функции распределения простых чисел Римана J(x) и суммировал первые 35 нетривиальных нуля дзета-функции Римана ζ(s). Мы видим, что периодический член заставляет функцию «резонировать» и начать приближаться к форме функции распределения простых чисел π(x).
Ниже показан тот же график с использованием большего количества нетривиальных нулей.
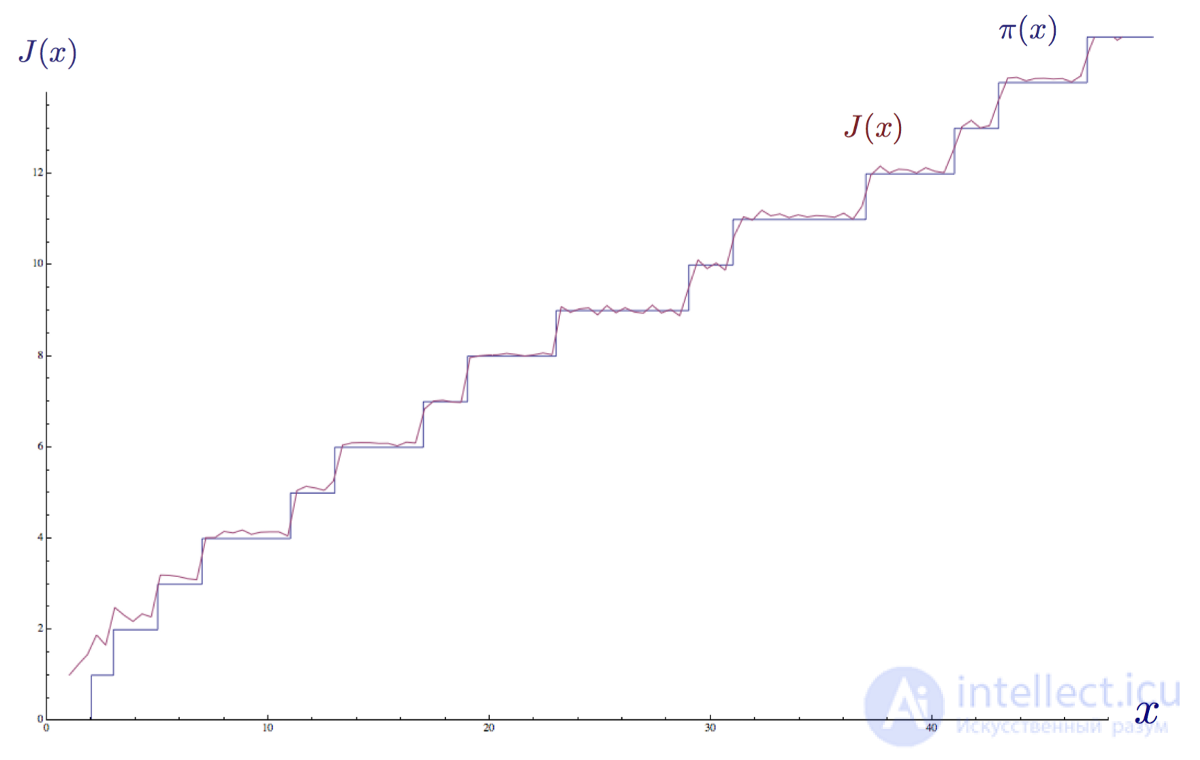
Ступенчатая функция распределения простых чисел π(x), аппроксимируемая явной формулой распределения простых чисел Римана J(x) с помощью первых 100 нетривиальных нулей ρ дзета-функции Римана.
С помощью явной функции Римана можно с очень большой точностью аппроксимировать количество простых чисел вплоть до заданного числа x. На самом деле, в 1901 году Нильс Кох доказал, что использование нетривиальных нулей дзета-функции Римана для коррекции погрешности функции интегрального логарифма эквивалентно «наилучшей» границе для величины погрешности в теореме о распределении простых чисел.
"… Эти нули действуют подобно телеграфным столбам, и особая природа дзета-функции Римана точно приказывает, как между ними должен висеть провод (ее график)...", — Дэн Рокмор
После смерти Римана в 1866 году всего лишь в возрасте 39 лет его новаторская статья продолжает оставаться ориентиром в области аналитической теории чисел и теории простых чисел. И по сей день гипотеза Римана о нетривиальных нулях дзета-функции Римана остается нерешенной, несмотря на активные исследования множества великих математиков. Каждый год публикуются связанные с этой гипотезой различные новые результаты и догадки в надежде, что когда-нибудь доказательство станет реальным
На этом все! Теперь вы знаете все про дзета-функция римана, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое дзета-функция римана и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Комментарии
Оставить комментарий
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Термины: Комплексный анализ и операционное исчисление (теория функций комплексного переменного)