Антиголоморфная функция

Привет, сегодня поговорим про антиголоморфная функция, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое антиголоморфная функция , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

Антиголоморфные функции (также называемые антианалитическими) — семейство функций, тесно связанных с голоморфными функциями.

Определение[править ]

Функция 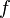, определенная на открытом подмножестве  комплексной плоскости, называется антиголоморфной, если ее производная  по 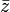 существует во всех точках этого множества. Это равносильно условию

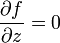
которым можно придать вид, аналогичный условиям Коши — Римана:

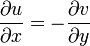
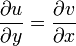
где

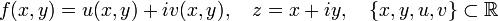
Функция, зависящая одновременно от 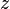 и 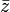, не является ни голоморфной, ни антиголоморфной.

Свойства[править ]

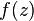•  голоморфна в  тогда и только тогда, когда 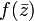 антиголоморфна в .
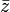• функция антиголоморфна тогда и только тогда, когда ее можно разложить по степеням  в окрестности каждой точки ее области определения.
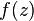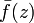•  голоморфна в  тогда и только тогда, когда  антиголоморфна в .
• если функция одновременно голоморфна и антиголоморфна, то она постоянна на любой связной компоненте ее области определения.

Литература[править ]

• Шабат Б. Об этом говорит сайт https://intellect.icu . В. Введение в комплексный анализ. — М.: Наука. — 1969, 577 стр.

На этом все! Теперь вы знаете все про антиголоморфная функция, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое антиголоморфная функция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)