Лекция
Привет, сегодня поговорим про дилогарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое дилогарифм , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
дилогарифм — специальная функция в математике, которая обозначается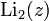 
и является частным случаем (n=2) полилогарифма 
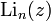. Дилогарифм определяется как
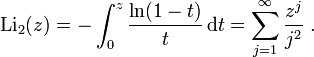
. В последние годы в самых разных задачах теории чисел, алгебры, топологии, геометрии мистическим образом появляется дилогарифм 
.
Вычисление дилогарифма по его разложению в ряд (х = РХ)
Приведенное определение дилогарифма верно для комплексных значений переменной z. Для действительных значений z=x у этой функции есть разрез вдоль действительной оси от 1 до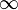 
. Обычно значение функции на разрезе определяется так, что мнимая часть дилогарифма отрицательна:
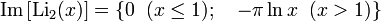
Функцию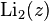 
часто называют дилогарифмом Эйлера, в честь Леонарда Эйлера, который рассмотрел эту функцию в 1768 году . Иногда дилогарифм называют функцией Спенса (Spence's function), в честь шотландского математикаУильяма Спенса (William Spence, 1777—1815) , который в начале XIX века исследовал функции, соответствующие 
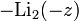и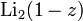 
. Название "дилогарифм" было введено Хиллом (C.J. Hill) в 1828 году.
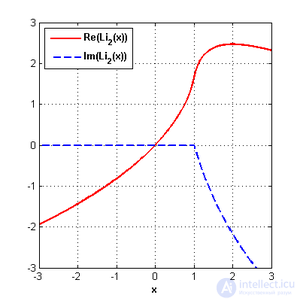
Действительная и мнимая части функции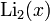 
Классический дилогарифм для комплексных чисел 
С 
определяется степенным рядом
.
Это может быть аналитическим продолжением на
Продолжать:
(Здесь, по тропинке в интегрироваться.)
Дилогарифм Блоха-Вигнера предназначен для 
определяется
.
Он четко выражен и устойчив даже в 
.
Он аналитик в 
, в 0 и 1 имеет особенности типа 
.
Дилогарифм Роджерса определяется
Для 
.
Другое распространенное определение:
.
Это зависит от первого через
все вместе.
Можно 
(прерывистый) полностью 
продолжить через 
и
Быть 
один больше 
заданная эллиптическая кривая . Об этом говорит сайт https://intellect.icu . Используя функцию Вейерштрассе , ее можно вычислить с помощью сетки
параметризовать через
мод 
.
Эллиптический дилогарифм 
тогда определяется как
,
в котором 
обозначает дилогарифм Блоха-Вигнера.
Эллиптический дилогарифм верен, за исключением рациональных кратных 
со значением 
совпадает с функцией L .
Для дилогарифма существует ряд полезных функциональных соотношений,
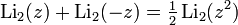
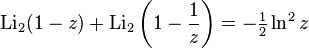
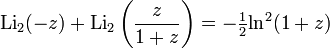
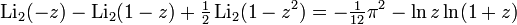
Для действительных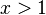 
,
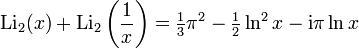
Известны также соотношения, содержащие две независимые переменные — например, тождество Хилла:
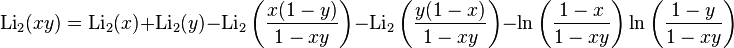
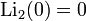
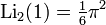
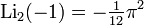
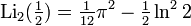
Используя соотношение между функциями от x и 1/x, получаем
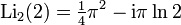
Существует также ряд результатов для аргументов, связанных с золотым сечением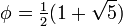 
,
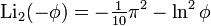
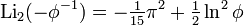
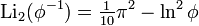
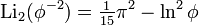
а также для дилогарифма мнимого аргумента,
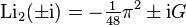
где G — постоянная Каталана.
Соотношения для частных значений
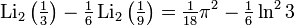
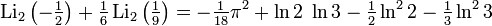
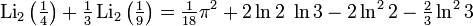
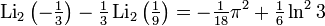
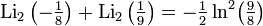
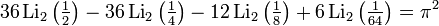
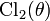
Возникает при рассмотрении дилогарифма, аргумент которого находится на единичной окружности в комплексной плоскости,
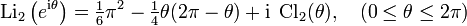
Таким образом,
![\operatorname{Cl}_2(\theta)=\operatorname{Im}\left[\operatorname{Li}_2\left(e^{{\rm i}\theta}\right)\right]
= {\textstyle{\frac{1}{2{\rm i}}}}\left[\operatorname{Li}_2\left(e^{{\rm i}\theta}\right)-\operatorname{Li}_2\left(e^{-{\rm i}\theta}\right)\right]](/th/25/blogs/id4261/38_39a3031ebd79874c3eca1eb64c899fc0.png)
Эта функция используется при вычислении объемов в гиперболической геометрии, и она связана с функцией Клаузена (а следовательно и с дилогарифмом),
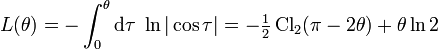
Иногда используется другое определение функции Лобачевского,
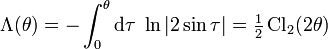
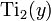
Возникает при рассмотрении дилогарифма мнимого аргумента,
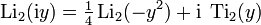
Таким образом,
![\operatorname{Ti}_2(y)=\operatorname{Im}\left[\operatorname{Li}_2({\rm i}y)\right]
= {\textstyle{\frac{1}{2{\rm i}}}}\left[\operatorname{Li}_2({\rm i}y)-\operatorname{Li}_2(-{\rm i}y)\right]](/th/25/blogs/id4261/43_301dd63c5eeba8c01653ec2f5cddf2fa.png)
Эта функция выражается через дилогарифмы как
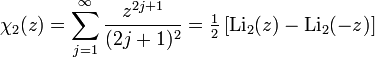
В частности,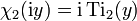 
.
описание физики часчтиц
На этом все! Теперь вы знаете все про дилогарифм, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое дилогарифм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Из статьи мы узнали кратко, но содержательно про дилогарифм
Комментарии
Оставить комментарий
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Термины: Комплексный анализ и операционное исчисление (теория функций комплексного переменного)