Тождество Эйлера - уравнение пяти констант (комплексный анализ) кратко

Привет, Вы узнаете о том , что такое тождество эйлера, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое тождество эйлера , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

тождество эйлера — частный случай формулы Эйлера при [⇨], известное тождество, связывающее пять фундаментальных математических констант - уравнение пяти констант:

где

— число е, или основание натурального логарифма,

— мнимая единица,

— пи, отношение длины окружности к длине ее диаметра,

— единица, нейтральный элемент по операции умножения,

— ноль, нейтральный элемент по операции сложения.

Тождество Эйлера названо в честь швейцарского, немецкого и российского математика Леонарда Эйлера[⇨]. Тождество считается образцом математической красоты[⇨], поскольку показывает глубокую связь между самыми фундаментальными числами в математике.

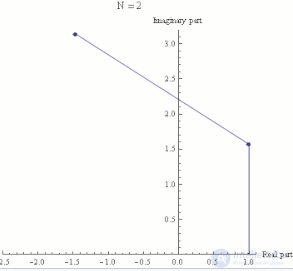
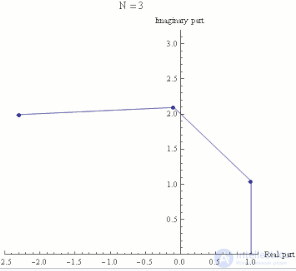
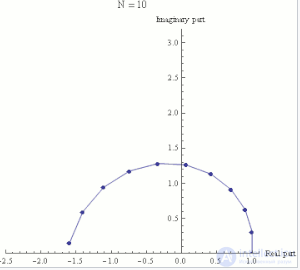
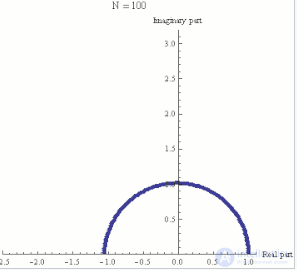
Экспоненциальная функция ez может быть определена как предел последовательности (1 + z/N)N, при N стремящемуся к бесконечности, и поэтому eiπ есть предел (1 + iπ/N)N. На каждом кадре этой анимации изображены числа (1 + iπ/N)k, где k пробегает от 0 до N, а N принимает различные возрастающие значения от 1 до 100.

Вывод

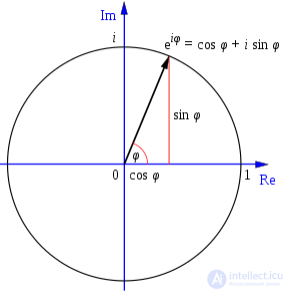
Тождество Эйлера — это особый случай формулы Эйлера из комплексного анализа:

для любого вещественного {\displaystyle x}. (Заметим, что аргументы тригонометрических функций и взяты в радианах). В частности

А из того, что

и

следует

что дает тождество:

Обобщения

Тождество Эйлера также является частным случаем более общего тождества: сумма корней из единицы -ой степени при равна :

Тождество Эйлера — это случай, когда .

В другой области математики, используя возведение в степень кватерниона, можно показать, что подобное тождество также применимо к кватернионам. Об этом говорит сайт https://intellect.icu . Пусть {i, j, k} — базисные элементы; тогда

В общем случае, если даны вещественные a1, a2, и a3 такие, что a12 + a22 + a32 = 1, то

Для октонионов, с вещественным an таким, что a12 + a22 + ... + a72 = 1, и с базисными элементами октонионов {i1, i2, ..., i7},

Математическая красота

Тождество Эйлера, объединяющее три основные математические операции (сложение, умножение и возведение в степень) и пять фундаментальных математических констант, принадлежащих к четырем классическим областям математики (числа и относятся к арифметике, мнимая единица — к алгебре, число — к геометрии, а число — к математическому анализу), произвело глубокое впечатление на научный мир, мистически истолковывалось как символ единства математики, и часто приводится как пример глубокой математической красоты.

Тождество Эйлера вызвало множество восторженных отзывов.

• Карл Фридрих Гаусс говорил, что если эта формула сразу не очевидна для студента, то он никогда не превратится в первоклассного математика.
• Профессор математики, натурфилософии и астрономии Гарвардского университета Бенджамин Пирс после доказательства на лекции тождества Эйлера заявил, что «это, наверное, правда, но она абсолютно парадоксальна; мы не можем понять ее, и мы не знаем, что она значит, но мы доказали ее, и поэтому мы знаем, что она должна быть достоверной»[3].
• Физик Ричард Фейнман называл (1977) тождество Эйлера «нашим сокровищем» и «самой замечательной формулой в математике».
• Профессор математики Стэнфордского университета Кит Девлин . в своем эссе «Самое прекрасное уравнение» (2002) сказал: «Как шекспировский сонет схватывает саму суть любви, или картина раскрывает красоту человеческой формы, намного более глубокую, чем просто кожа, уравнение Эйлера проникает в самые глубины существования».
• Почетный профессор Университета Нью-Гемпшира Пол Нахин . в своей книге, посвященной формуле Эйлера и ее применению в анализе Фурье, описывает тождество Эйлера как «изысканной красоты».
• По мнению популяризатора математики Констанс Рид, это тождество является «самой знаменитой формулой во всей математике».

Опрос читателей, проведенный математическим журналом The Mathematical Intelligencer в 1990 году, назвал тождество Эйлера «самой красивой теоремой в математике». В другом опросе читателей, проведенном физическим журналом PhysicsWorld в 2004 году, тождество Эйлера (вместе с уравнениями Максвелла) было названо «величайшим уравнением в истории».

Исследование мозга шестнадцати математиков показало, что «эмоциональный мозг» (в частности, медиальная орбитофронтальная кора, реагирующая на прекрасную музыку, поэзию, картины и т. д.) активировался более последовательно в случае тождества Эйлера, чем в отношении любой другой формулы[9].

История

Формула Эйлера, из которой сразу следует тождество Эйлера, впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году (когда Эйлеру было 7 лет), и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum) в 1722 году.

Эйлер опубликовал формулу Эйлера в ее привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748).

Однако, в работах Эйлера 1740 и 1748 годов не фигурирует именно тождество Эйлера (в его нынешнем классическом виде), где возможно, что он его никогда не выводил. Есть вероятность, что Эйлер мог получить информацию о формуле Эйлера через своего швейцарского соотечественника Иоганна Бернулли.

По мнению Робина Уилсона (англ.) :

Мы видели, как оно [тождество Эйлера] может быть легко выведено из результатов Иоганна Бернулли и Роджера Котса, но, похоже, ни один из них этого не сделал. Даже Эйлер, кажется, не записал этого в явном виде — и, конечно, оно не фигурирует ни в одной из его публикаций — хотя он, несомненно, понял, что это немедленно следует из его тождества [в данном случае — формулы Эйлера], eix = cos x + i sin x. Более того, кажется, неизвестно, кто первым сформулировал результат явно…

В культуре

• Тождеству Эйлера посвящен фильм Такаси Коидзуми[en] «Любимое уравнение профессора».

См. Также

• Формула де Муавра
• Экспоненциальная функция
• Постоянная ГельфондаБ
• Бета-функцияГ
• Гамма-функция
• Гауссов интегралД
• Диаграмма Эйлера
• Диск ЭйлераЗ
• Золотая медаль имени Леонарда ЭйлераК
• Клотоида
• Критерий Эйлера
• Международный математический институт имени Л. Эйлера
• Метод Эйлера
• Окружность девяти точек
• Подстановки Эйлера
• Постоянная Эйлера — Маскерони
• Проект Эйлер
• Прямая Эйлера
• Счастливые числа Эйлера
• Теорема вращения Эйлера
• Теорема Эйлера (теория чисел)
• Теорема Эйлера для многогранников
• Теорема Эйлера о треугольнике
• Тождество Эйлера (комплексный анализ)
• Углы Эйлера
• Уравнение Коши — Эйлера
• Уравнение Эйлера
• Уравнение Эйлера — Лагранжа
• Уравнения Эйлера
• Формула Эйлера
• Формула Эйлера (дифференциальная геометрия)
• Формула Эйлера для радиальных турбин и центробежных насосов
• Функция Эйлера
• Числа Эйлера I рода
• Число Эйлера (физика)
• (2002) Эйлер
• Эйлеров цикл
• Эйлерова характеристика
• E (число)

Исследование, описанное в статье про тождество эйлера, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое тождество эйлера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)

Из статьи мы узнали кратко, но содержательно про тождество эйлера