Некоторые применения операционного исчисления кратко

Привет, сегодня поговорим про применение операционного исчисления, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое применение операционного исчисления , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

1. Решение задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами

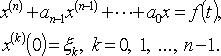
Применяя преобразование Лапласа и используя теорему о дифференцировании оригинала, приходим к уравнению

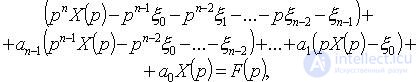
где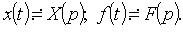

Преобразуя, получаем уравнение вида 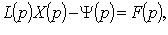откуда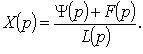

Из последнего соотношения получаем возможность найти оригинал x(t) по его изображению X(p).

Начальная задача 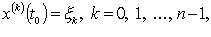сводится заменой 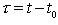к описанной.

2. Об этом говорит сайт https://intellect.icu . Решение задачи Коши для систем линейных дифференциальных уравнений с постоянными коэффициентами. Схема применения преобразования Лапласа такая же, как в п. 1.

Пример.

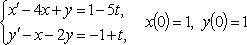
Применяя преобразование Лапласа, приходим к алгебраической системе:

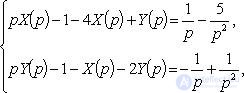
откуда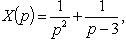

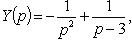
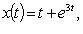
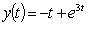
3. Решение интегральных уравнений Вольтера типа свертки

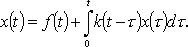
Применяя преобразование Лапласа, получаем

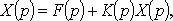
где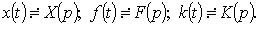

Из последнего уравнения выразим X(p) и по X(p) найдем оригинал x(t) - решение интегрального уравнения.

4. Вычисление несобственных интегралов.

Если f = F, g = G, то

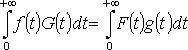
(формула Парсеваля).

Вау!! 😲 Ты еще не читал? Это зря!

• Решение задачи Коши операционным методом общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,

На этом все! Теперь вы знаете все про применение операционного исчисления, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое применение операционного исчисления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)