4.1.1. Общие понятия дифференциальных уравнений первого порядка. Задача Коши. примеры решения кратко

Привет, мой друг, тебе интересно узнать все про общие понятия дифференциальных уравнений первого порядка, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое общие понятия дифференциальных уравнений первого порядка, задача коши, дифференциальные уравнения первого порядка, ду первого порядка , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальные уравнения.

Дифференциальное уравнение первого порядка имеет вид F(x,y,y') или y' = f(x,y) , где y - неизвестная функция от переменной x.

Функция y = φ(x) называется решением дифференциального уравнения, если при подстановке y = φ(x) и ее производной в данное уравнение получается тождество.

Совокупность всех решений дифференциального уравнения называется общим решением. Оно представляется в виде некоторой функции y = φ(x,c) (c - постоянная). При надлежащем выборе постоянной c функция φ(x,c) задает любое частное решение.

Задача нахождения решения дифференциального уравнения, удовлетворяющего начальному условию y(x₀) = y₀ , называется задачей Коши.

Постановка Задачи Коши

задача коши — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при , а решение отыскивается при .

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее задачу Коши можно рассматривать как одну из краевых задач.

Основные вопросы, которые связаны с задачей Коши, таковы:

1. Существует ли (хотя бы локально) решение задачи Коши?
2. Если решение существует, то какова область его существования?
3. Является ли решение единственным?
4. Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?

Говорят, что задача Коши имеет единственное решение, если она имеет решение и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки имеет поле направлений, совпадающее с полем направлений . Точка задает начальные условия.

Различные постановки задачи Коши

• О ду первого порядка , разрешенное относительно производной

• Система ОДУ первого порядка, разрешенная относительно производных (нормальная система -го порядка)

• ОДУ n-го порядка, разрешенное относительно старшей производной

Теоремы о разрешимости задачи Коши для ОДУ

Пусть в области рассматривается задача Коши:

где . Об этом говорит сайт https://intellect.icu . Пусть правая часть является непрерывной функцией в . В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши: Пусть a>0 и b>0 таковы, что замкнутый прямоугольник

принадлежит области D, тогда на отрезке , где , , существует решение задачи Коши.

Указанный отрезок называется отрезком Пеано. Заметим, что, локальный характер теоремы Пеано не зависит от гладкости правой части. Например, для и для решение существует лишь на интервале . Также отметим, что без дополнительных предположений относительно гладкости правой части нельзя гарантировать единственность решения задачи Коши. Например, для возможно более одного решения.

Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x, y) удовлетворяет условию Липшица на D относительно y, если существует постоянная L такая, что

для всех .

Пусть правая часть f(x, y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.

Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.

Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию

где A>0 — константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.

Теоремы о разрешимости задачи Коши для дифференциальных уравнений в частных производных[

Пусть поставлена задача Коши:

,

где S - начальная гиперповерхность, , - n-мерные векторы. Тогда условие локальной разрешимости этой задачи Коши можно сформулировать следующим образом:

Решение задачи Коши в окрестности точки ∈ S существует и единственно, если проходящая через точку характеристика трансверсальна поверхности S

Пример 1

Найти решение задачи Коши методами операционного исчисления

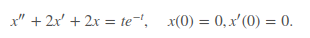
РЕШЕНИЕ:
Перейдем к изображениям:

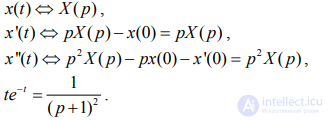
Подставляем все и получаем обычное уравнение:

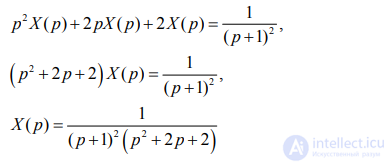
Разложим дробь 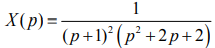на сумму простейших дробей методом неопределенных коэффициентов:

Приравниваем коэффициенты при одинаковых степенях p справа и слева и получаем систему для нахождения коэффициентов:

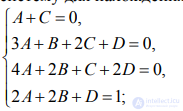
Находим решение:


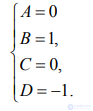
Получили

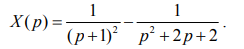
Возвращаемся к оригиналам:

Решение задачи Коши:

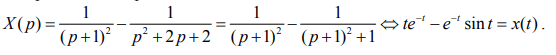
Пример 2 Найти решение задачи Коши

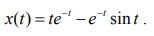
y″ = 8·sin³y·cosy, y(1) = π/2, y′(1) = 2.

Решение.

Это дифференциальное уравнение, допускающее понижение порядка. Порядок дифференциального уравнения может быть понижен при помощи замены

y′ = p(y).

Тогда y″ = p·p′ .

После подстановки, дифференциальное уравнение запишется p·p′ = 8sin³ycosy .

Это дифференциальное уравнение с разделяющимися переменными. Разделим переменные в полученном дифференциальном уравнении
p·dp = 8sin³ycosy dy.

Интегрируем последнее дифференциальное уравнение. ∫p·dp = ∫8sin³ycosy dy.

После интегрирования, получим p² = 4sin⁴y + С,

Подставим начальные условия. При y = π/2, p = y′ = 2. Тогда 4 = 4sin⁴(π/2) + С, или C = 0.
В результате, после подстановки C в найденное решение и извлечения корня с обеих сторон, получаем y′ = p = 2sin²y.

Получили дифференциальное уравнение первого порядка с разделяющимися переменными.

Разделим переменные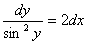 и проинтегрируем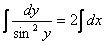

В результате получим ctg y = −2x + C₁.

Подставим начальные условия. При y = π/2, x = 1. Тогда ctg(π/2) = −2 + C₁, или C₁ = 2.

Искомое решение задачи Коши для исходного дифференциального уравнения второго порядка принимает вид

ctg y = 2−2x, или y = arctg(2−2x).

Ответ: y = arctg(2−2x).

Вау!! 😲 Ты еще не читал? Это зря!

• Обыкновенное дифференциальное уравнение
• Особое решение
• Краевая задача
• Метод Эйлера метод эйлера , уточненный метод эйлера , ]
• Метод Рунге — Кутты метод рунге-кутты , ]
• Теорема Пеано
• Операционное исчисление

Тебе нравиться общие понятия дифференциальных уравнений первого порядка? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое общие понятия дифференциальных уравнений первого порядка, задача коши, дифференциальные уравнения первого порядка, ду первого порядка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальные уравнения

Из статьи мы узнали кратко, но содержательно про общие понятия дифференциальных уравнений первого порядка

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.