Лекция
Привет, мой друг, тебе интересно узнать все про ы решения задач к разделу дифференциаоьные уравнения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ы решения задач к разделу дифференциаоьные уравнения , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальные уравнения.
Пример N 1
Найти общее решение уравнения 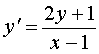 .
.
Решение.
Так как 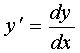 , то уравнение имеет вид :
, то уравнение имеет вид : 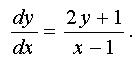
Домножив все уравнение на dx, получим: 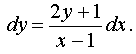
Разделив все уравнение на 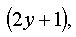 приходим к уравнению с разделяющимися переменными :
приходим к уравнению с разделяющимися переменными : 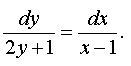
Интегрируя, получим :
Ответ:
Пример N 2
Найти общее решение уравнения 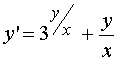 .
.
Решение.
Уравнение является однородным, так как функция, стоящая в правой части, является однородной:
.
Сделаем подстановку: 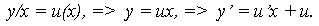
Преобразуем исходное уравнение:
Получили уравнение с разделяющимися переменными: 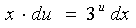 . Делим уравнение на
. Делим уравнение на 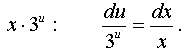
Интегрируя почленно, получим:
Ответ:
Пример N 3
Найти общее решение уравнения y' + 3x2 y + x2 = 0 .
Решение.
Уравнение является линейным относительно функции у и ее производной y'. Об этом говорит сайт https://intellect.icu . Решение ищем в виде y = u · v , где u и v √ функции от х. Так как 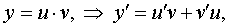 то исходное уравнение примет вид:
то исходное уравнение примет вид: 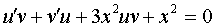 или
или 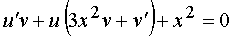 .
.
Функцию v находим из уравнения 3x2v + v' = 0, при этом исходное уравнение упрощается: u'v + x2 = 0. Находим функцию v :
Функцию находим из уравнения u'v + x2 = 0 с 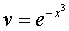 :
:
Ответ:
Пример N 4
Решить задачу Коши: y" + y = х, y(0) = 1, y'(0) = 1.
Решение.Это неоднородное линейное уравнение с постоянными коэффициентами. Его решение является суммой y0 - общего решения уравнения y" + y = 0 и y* - частного решения данного уравнения.
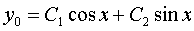 .
. 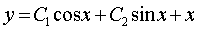 - общее решение.
- общее решение.Подставляя найденные постоянные С1 и С2 в общее решение, получаем решение задачи Коши: 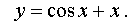
Ответ:
Пример N 5
Найти общее решение дифференциального уравнения: 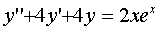 .
.
Решение.
Общее решение исходного уравнения, равного сумме общего решения однородного уравнения y0 и частного решения y* .
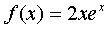 , (α = 1 не является корнем характеристического уравнения, степень многочлена равна одному), то частное решение y* ищем в виде:
, (α = 1 не является корнем характеристического уравнения, степень многочлена равна одному), то частное решение y* ищем в виде: 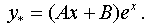
Подставляя y* , y*', y*" в исходное уравнение, получаем:
Разделив на ex , после приведения подобных получим:
Сравнивая коэффициенты при одинаковых степенях, составляем систему линейных алгебраических уравнений:
найдя решение этой системы:
записываем общее решение:
Ответ:
Тебе нравиться ы решения задач к разделу дифференциаоьные уравнения? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое ы решения задач к разделу дифференциаоьные уравнения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальные уравнения
Из статьи мы узнали кратко, но содержательно про ы решения задач к разделу дифференциаоьные уравнения
Комментарии
Оставить комментарий
Математический анализ. Дифференциальные уравнения
Термины: Математический анализ. Дифференциальные уравнения