4.2.2. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами

Привет, мой друг, тебе интересно узнать все про неоднородные линейные уравнения второго порядка с постоянными коэффициентами, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое неоднородные линейные уравнения второго порядка с постоянными коэффициентами , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальные уравнения.

Общим решением неоднородного линейного уравнения второго порядка y" + py' + qy = f(x) является сумма общего решения y₀ однородного уравнения и частного решения y_* данного уравнения, т.е. y = y₀ + y_* .

Если правая часть f(x) уравнения представляет собой произведение e^{α · x} P_n(x) , где α - число, P_n(x) - многочлен степени n , тогда частное решение y_* находится подбором неопределенных коэффициентов многочлена 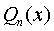   степени n .

1. Если число α не является корнем характеристического уравнения k² + pk + q = 0 , тогда    .
2. Если число α - однократный корень характеристического уравнения k² + pk + q = 0 , тогда   
3. Если число α - двукратный корень характеристического уравнения k² + pk + q = 0 , тогда   

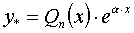Пусть f(x) имеет вид:

где P(x), R(x) - многочлены.

Пусть n - наибольшая степень этих многочленов. Об этом говорит сайт https://intellect.icu . Частное решение y_* находится подбором неопределенных коэффициентов многочленов U_n(x), V_n (x) степени n : 
  1)   если числа a ± ib не являются корнями характеристического уравнения k² + pk + q = 0 , тогда

;

  2)   если числа a ± ib - корни характеристического уравнения k² + pk + q = 0 , тогда

.

 

Выбрав вид частного решения y_* , соответствующий правой части f(x) дифференциального уравнения, находим y_*^', y_*^"

Подставив найденные для y_* , y_*^' , y_*^" выражения в исходное линейное уравнение второго порядка, определяем неизвестные коэффициенты многочлена    , или многочленов U(x)  и  V(x) .

Тебе нравиться неоднородные линейные уравнения второго порядка с постоянными коэффициентами? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое неоднородные линейные уравнения второго порядка с постоянными коэффициентами и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальные уравнения

Из статьи мы узнали кратко, но содержательно про неоднородные линейные уравнения второго порядка с постоянными коэффициентами