Операционное исчисление . Таблица основных преобразований Лапласа кратко

Привет, сегодня поговорим про операционное исчисление, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое операционное исчисление, таблица основных преобразований лапласа, преобразования лапласа , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

операционное исчисление — один из методов математического анализа, позволяющий в ряде случаев с помощью весьма простых средств решать сложные математические задачи.

История

В середине XIX века появился ряд сочинений, посвященных так называемому символическому исчислению и применению его к решению некоторых типов линейныхдифференциальных уравнений. Сущность символического исчисления состоит в том, что вводятся в рассмотрение и надлежащим образом интерпретируются функции оператора дифференцирования 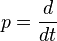(см. Операторное исчисление). Среди сочинений по символическому исчислению следует отметить вышедшую в 1862 году вКиеве обстоятельную монографию украинского математика М. Е. Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений». В ней поставлены и разрешены основные задачи того метода, который в дальнейшем получил название операционного.

В 1892 году появились работы английского ученого О. Хевисайда, посвященные применению метода символического исчисления к решению задач по теории распространения электрических колебаний в проводах. В отличие от своих предшественников, Хевисайд определил обратный оператор однозначно, полагая 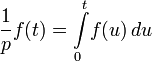и счита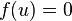я для 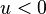. Труды Хевисайда положили начало систематическому применению символического, или операционного, исчисления к решению физических и технических задач.

Однако широко развитое в трудах Хевисайда операционное исчисление не получило математического обоснования, и многие его результаты оставались недоказанными. Строгое обоснование было дано значительно позже, когда была установлена связь между функциональным преобразованием Лапласа 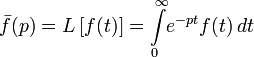и оператором дифференцирования 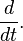Именно, если существует производная 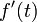, для которой 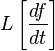существует и 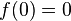, то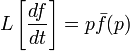

Операционное исчисление представляет собой метод интегрирования некоторых классов линейных дифференциальных уравнений, который состоит в том, что сначала ищут не саму неизвестную функцию, которая удовлетворяет дифференциальное уравнение, а некоторую соответствующую опцию, преобразованную по Лапласу. Этот метод непосредственно применяется также для решения некоторых типов линейных уравнений в частных производных, а также разностных, дифференциально-разностных уравнений и некоторых типов интегральных уравнений.
Построение операционного исчисления базируется на идее преобразования функции действительной переменной t, что называется оригиналом, в функцию комплексной переменной p, что называется изображением.

Свойства изображений

• Линейность

Оригинал линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.

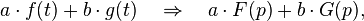
где a и b – произвольные комплексные числа.

• Теорема подобия

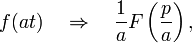
где a>0.

• Дифференцирование оригинала

• Дифференцирование изображения

• Интегрирование оригинала

• Интегрирование изображения

• Теорема смещения

• Теорема запаздывания

• Теорема умножения (свертки)

Изображения различных функций

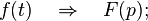
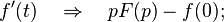
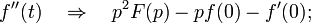
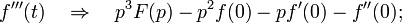
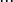
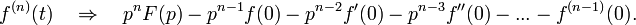
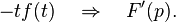
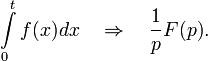
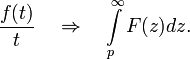
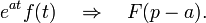
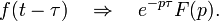
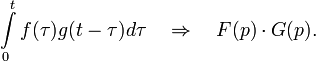
Оригинал	Изображение		Оригинал	Изображение		Оригинал	Изображение

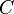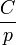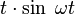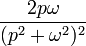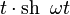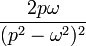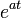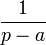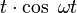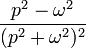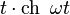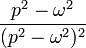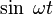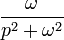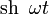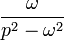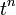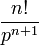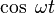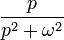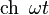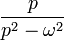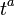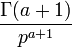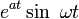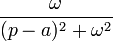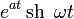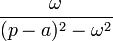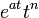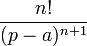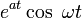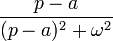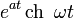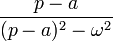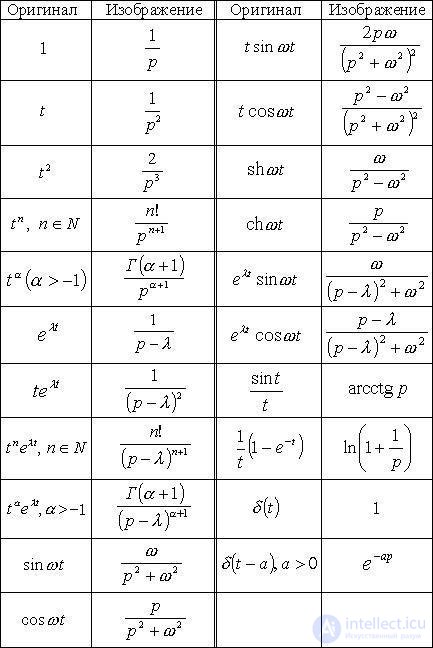
таблица основных преобразований лапласа

Пример применения операторных методов

Задача

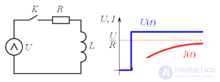
На рисунке изображена коммутируемая RL-цепочка. Об этом говорит сайт https://intellect.icu . В некоторый момент времени t=0 ключ К замыкается. Определить зависимость тока в RL-цепочке от времени.

Решение традиционным методом

Согласно второму закону Кирхгофа, схема описывается следующим дифференциальным уравнением:

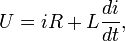
где первый член описывает падение напряжения на резисторе R, а второй - на индуктивности L.

Делаем замену переменной 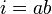и приводим уравнение к виду:

Поскольку один из сомножителей a, b можно выбрать произвольно, выберем b так, чтобы выражение в скобках было равно нулю:

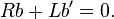
Разделяем переменные:

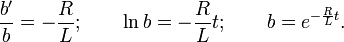
С учетом выбранного значения b дифференциальное уравнение приводится к виду

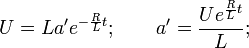
Интегрируя, получаем

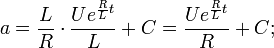
Получаем выражение для тока

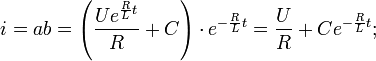
Значение постоянной интегрирования находим из условия, что в момент t=0 тока в цепи не было:

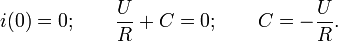
Окончательно получаем

Решение операторным методом

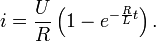
Найдем изображения каждого из слагаемых дифференциального уравнения:

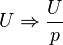получается потому, что изменение U во времени выражается функцией U = H(t)U (ключ замкнули в момент t = 0), где H(t) - ступенчатая функция Хевисайда, (H(t) = 0 при t < 0 и H(t) = 1 при t = 0 и t > 0, причем изображение H(t) есть 1/p).

Получаем следующее изображение дифференциального уравнения

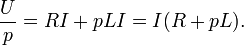
Из последнего выражения найдем изображение тока:

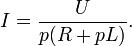
Таким образом, решение сводится к нахождению оригинала тока по известному изображению. Разложим правую часть уравнения на элементарные дроби:

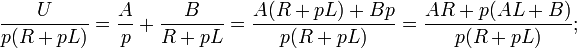
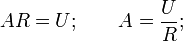
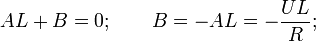
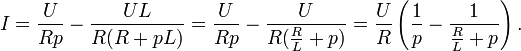
Найдем оригиналы элементов последнего выражения:

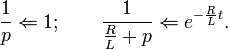
Окончательно получаем

Вывод

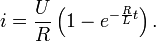
Операционное исчисление чрезвычайно удобно в электротехнике для расчета динамических режимов различных цепей. Алгоритм расчета следующий.

1) Все элементы цепи рассматриваем как сопротивления Z_i, величины которых находим исходя из изображений переходных функций соответствующих элементов.

Например, для резистора:

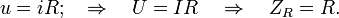
Для индуктивности:

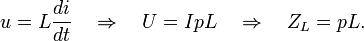
Для емкости:

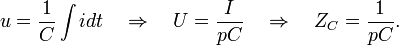
2) Используя указанные значения сопротивлений, находим изображения токов в цепи, используя стандартные методы расчета цепей, применяемые в электротехнике.

3) Имея изображения токов в цепи, находим оригиналы, которые и являются решением дифференциальных уравнений, описывающих цепь.

Замечания

Интересно отметить, что полученные выше выражения для операторного сопротивления различных элементов с точностью до преобразования

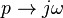
совпадают с соответствующими выражениями для сопротивлений в цепях переменного тока:

Вау!! 😲 Ты еще не читал? Это зря!

• Решение задачи Коши операционным методом общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
• применение операционного исчисления ,

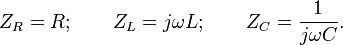
На этом все! Теперь вы знаете все про операционное исчисление, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое операционное исчисление, таблица основных преобразований лапласа, преобразования лапласа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)

Из статьи мы узнали кратко, но содержательно про операционное исчисление