Эллиптический интеграл сущность и области применения кратко

Привет, Вы узнаете о том , что такое эллиптический интеграл, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое эллиптический интеграл , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

Эллипти́ческий интегра́л — некоторая функция f над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:

,

где R — рациональная функция двух аргументов, P — квадратный корень из многочлена 3-й или 4-й степени, не имеющего кратных корней, c — некоторая константа из поля, где определена функция.

В общем случае эллиптический интеграл не может быть формально выражен в элементарных функциях. Исключением являются случаи, когда P имеет кратные корни или когда многочлены в R(x,y) не содержат нечетных степеней y .

Однако для каждого эллиптического интеграла существуют формулы приведения его к сумме элементарных функций и от одного до трех нормальных эллиптических интегралов, называемых эллиптическими интегралами 1-го, 2-го и 3-го рода).

В интегральном исчислении эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно, а позднее — Леонардом Эйлером.

Эллиптические интегралы часто представляют в виде функции ряда различных аргументов. Эти различные аргументы полностью эквивалентны (они дают одни и те же интегралы), но может возникнуть путаница, связанная с их различным происхождением. В большинстве работ авторы придерживаются канонического наименования. Прежде чем определить сами интегралы, необходимо ввести наименования для аргументов:

• α — модулярный угол (иногда модулярный угол обозначается лигатурой oε);
• — модуль эллиптического интеграла;
• — параметр.

Следует отметить, что нормальные эллиптические интегралы Лежандра, как полные, так и неполные, являются четными функциями модуля k (и модулярного угла α). Их область определения −1≤k≤+1.

Иногда, преимущественно в советской научной литературе, под параметром эллиптического интеграла подразумевают характеристику нормального эллиптического интеграла Лежандра 3-го рода (напр., Корн Г., Корн Т. «Справочник по математике для научных работников и инженеров»).

Заметим, что представленные выше величины определяются одна через другую; определение одной из них задает и две остальные.

Эллиптический интеграл зависит также и от другого параметра, который, как и предыдущий, можно ввести несколькими способами:

• где sn — эллиптическая функция Якоби;
• — амплитуда;

Определение одного из этих параметров определяет остальные. Таким образом, они могут использоваться вперемешку. Заметим, что u зависит также и от m. Несколько дополнительных уравнений связывают u с другими параметрами:

и

Последнее иногда называется дельта амплитуда и записывается как

Иногда в литературе ссылаются на дополнительный параметр, дополнительный модуль или дополнительный модулярный угол. Их вводят следующим способом:

• — дополнительный параметр;
• — дополнительный модуль;
• — дополнительный модулярный угол.

Нормальный эллиптический интеграл Лежандра 1-го рода F определяется как

,

или, в форме Якоби,

.

Обозначения эллиптических интегралов не являются универсально общепринятыми. Следует различать такие разделители между переменной и параметром, как «\», «|» и «,». Там, где в качестве разделителя используется вертикальная черта, за ней ставится параметр интеграла, тогда как за обратной косой чертой ставится модулярный угол. В частности, верно соотношение

.

;

;

;

;

Нормальный эллиптический интеграл Лежандра 2-го рода E определяется как

или, используя подстановку x=sin⁡φ,

E(φ,0)=φ ;

E(iφ,0)=iφ ;

E(φ,1)=sin⁡φ ;

E(iφ,1)=i sh ⁡φ .

Нормальный эллиптический интеграл Лежандра 3-го рода Π определяется как

или

Число c называется характеристикой и может принимать любое значение, независимо от остальных аргументов. Свойства эллиптического интеграла 3-го рода существенно зависят от величины характеристики. Заметим, что значение интеграла стремится к бесконечности для любых m.

Введем дополнительные обозначения:

;

;

;

;

;

K(α) — полный нормальный эллиптический интеграл Лежандра 1-го рода.

Тогда можно записать интеграл через тета-функции Якоби:

где

и

С помощью подстановки этот случай сводится к предыдущему, так как

Введем дополнительно величину

Тогда:

Введем дополнительные обозначения:

q=q(α);

Тогда эллиптический интеграл равен:

где

и

С помощью подстановки этот случай сводится к предыдущему, так как

Введем дополнительно величину

Тогда:

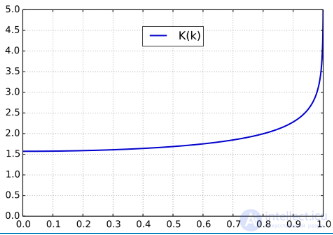
В случае, если амплитуда φ нормального эллиптического интеграла Лежандра 1-го рода равна π/2, он называется полным нормальным эллиптическим интегралом Лежандра 1-го рода:

или

Полный эллиптический интеграл 1-го рода можно представить в виде степенного ряда:

что эквивалентно выражению

где n!! обозначает двойной факториал.

Полный эллиптический интеграл 1-го рода можно записать через гипергеометрическую функцию следующим образом:

.

.

где E(k) — полный нормальный эллиптический интеграл Лежандра 2-го рода, определенный в следующем разделе.

Полный эллиптический интеграл 1-го рода является решением дифференциального уравнения

Вторым решением этого уравнения является

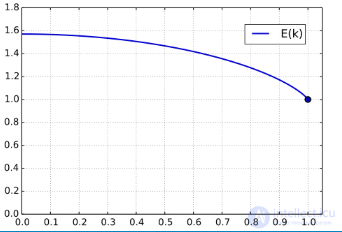
В случае, если амплитуда φ нормального эллиптического интеграла Лежандра 2-го рода равна π/2 , он называется полным нормальным эллиптическим интегралом Лежандра 2-го рода:

или

Полный эллиптический интеграл 2-го рода можно представить в виде степенного ряда:

что эквивалентно выражению

Полный эллиптический интеграл 2-го рода можно записать через гипергеометрическую функцию следующим образом:

E(1)=1.

Полный эллиптический интеграл 2-го рода является решением дифференциального уравнения

Вторым решением этого уравнения является функция

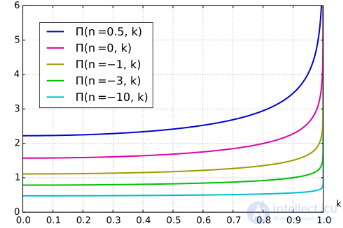
Аналогично полным эллиптическим интегралам 1-го и 2-го рода можно ввести полный эллиптический интеграл 3-го рода:

или

,

где — дзета-функция Якоби.

где — лямбда-функция Хеймана.

или

Практические применение эллиптического интеграла

Эллиптические интегралы — это не просто абстрактная математика. Об этом говорит сайт https://intellect.icu . Они возникают естественно во многих реальных физических, геометрических и инженерных задачах. Ниже — краткий, но систематичный обзор:

1. Геометрия и длины дуг

Классическое происхождение эллиптических интегралов — вычисление длины эллипса.

Пример:

Длина эллипса с полуосями a,ba, ba,b:

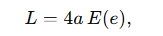
где 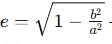— эксцентриситет,
а E(e) — эллиптический интеграл второго рода.

Нельзя выразить длину эллипса через элементарные функции, только через эллиптические.

2. Физика колебаний и маятники

Реальный (не малый!) математический маятник описывается уравнением:

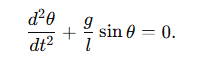
Решение выражается через обратные эллиптические функции Якоби (а период через K(k) ):

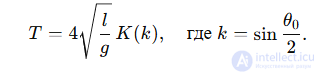
То есть при больших амплитудах период маятника увеличивается, и формула 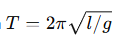становится неточной.

3. Электродинамика, магнитные поля, потенциалы

В задачах вычисления взаимной индукции, поля кольцевого тока, вихревых токов эллиптические интегралы описывают:

• магнитное поле по оси кольца,

• поток через виток,

• индуктивность между коаксиальными кольцами.

Например, для кольцевого проводника радиуса aaa и наблюдателя на расстоянии rrr:

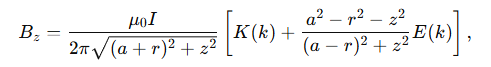
где k зависит от геометрии.

4. Механика, орбиты и небесная механика

Эллиптические интегралы появляются при:

• вычислении траекторий под действием обратноквадратичных сил (орбиты, гравитация);

• расчетах времени движения по орбите;

• моделировании прецессии и нутации.

5. Теория потенциала, интегралы поверхностей

При решении интегралов типа:

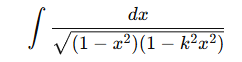
или при параметризации эллиптических цилиндров и поверхностей второго порядка.

6. Электроника и сигналы

В теории фильтров:

• Эллиптические фильтры (Cauer filters) названы именно из-за связи их амплитудной характеристики с эллиптическими функциями Якоби.

• Формулы расчета параметров фильтров включают K(k) и E(k).

7. Современные вычислительные и графические применения

• в моделировании деформаций (анизотропные поверхности);

• при генерации эллиптических контуров и поверхностей в 3D-графике;

• в аналитической геометрии кривых второго порядка.

8. Чистая математика

Эллиптические интегралы и их обратные функции (функции Якоби, Вейерштрасса) — фундамент эллиптических кривых, на которых основана:

• современная криптография (ECC),

• теория чисел (модулярные формы, теорема Ферма–Вайля–Тейта).

• эллиптическая функция ,
• Эллиптическая кривая
• Специальные функции
• Аппроксимации эллиптических интегралов

Исследование, описанное в статье про эллиптический интеграл, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое эллиптический интеграл и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)

Из статьи мы узнали кратко, но содержательно про эллиптический интеграл