Полилогарифм функция, график, значения кратко

Привет, сегодня поговорим про полилогарифм, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое полилогарифм , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

полилогарифм — специальная функция, обозначаемая 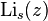и определяемая как бесконечный степенной ряд

где s и z — комплексные числа, причем . Для иных z делается обобщение с помощью аналитического продолжения.

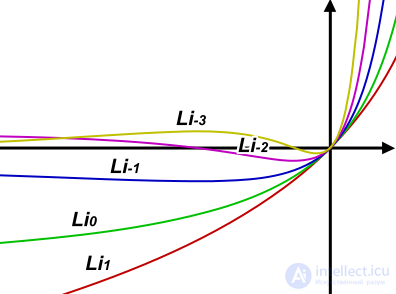
В математике , то полилогарифм (также известный как функции Jonquiere в , для Альфреда Jonquiere) является специальной функцией Li сек ( г ) порядка s и аргумента г . Только для специальных значений s полилогарифм сводится к элементарной функции, такой как натуральный логарифм или рациональные функции . В квантовой статистике , функция полилогарифм выступает в качестве замкнутой форме интегралов в распределении Ферми-Дирака и распределения Бозе-Эйнштейнаи также известен как интеграл Ферми – Дирака или интеграл Бозе – Эйнштейна . В квантовой электродинамике полилогарифмы положительного целого порядка возникают при расчете процессов, представленных диаграммами Фейнмана высших порядков .

Функция полилогарифма эквивалентна дзета-функции Гурвица - любая функция может быть выражена через другую - и обе функции являются частными случаями трансцендента Лерха . Полилогарифмы не следует путать ни с полилогарифмическими функциями, ни со смещенным логарифмическим интегралом, который имеет те же обозначения, но с одной переменной.

Карта высот полилогарифма на комплексной плоскости

Частным случаем является 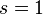, при котором 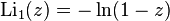. Функци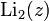и и 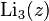получили названия дилогарифма и трилогарифма соответственно. Для полилогарифмов различных порядков справедливо соотношение

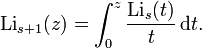
Альтернативными определениями полилогарифма являются интегралы Ферми — Дирака и Бозе — Эйнштейна.

Частные значения

Отношение к другим функциям

• При z = 1 полилогарифм сводится к дзета-функции Римана

• Полилогарифм связан с функцией эты Дирихля и Дирихлем беты - функцией :

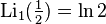
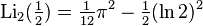
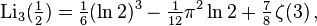
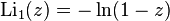
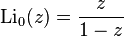
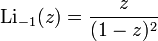
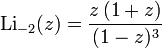
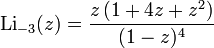
где η ( s ) - эта функция Дирихле. Об этом говорит сайт https://intellect.icu . Для чисто мнимых аргументов мы имеем:

где β ( s ) - бета-функция Дирихле.

• Полилогарифм связан с полным интегралом Ферми – Дирака как:

• Полилогарифм является частным случаем неполной функции полилогарифма

• Полилогарифм является частным случаем трансцендента Лерха ( Erdélyi et al. 1981 , § 1.11-14)

• Полилогарифм связан с дзета-функцией Гурвица следующим образом:

отношении которых, однако, признана недействительной в положительное целое число с помощью полюсов в гамма - функции Г (1- з ), а при х = 0 полюса обоих дзета - функций; вывод этой формулы дан под представлениями серии ниже. С небольшой помощью функционального уравнения для дзета-функции Гурвица полилогарифм, следовательно, также связан с этой функцией через ( Jonquière 1889 ):

какое соотношение имеет место для 0 ≤ Re ( x ) <1, если Im ( x ) ≥ 0, и для 0 x ) ≤ 1, если Im ( x ) <0. Эквивалентно, для всех комплексов s и для комплекса z ∉] 0; 1], формула обращения гласит:

и для всего комплекса s и для комплекса z ∉] 1; ∞ [

Для z ∉] 0; ∞ [ln (- z ) = −ln (- 1 ⁄ z ), и оба выражения совпадают. Эти соотношения дают аналитическое продолжение полилогарифма за пределами круга сходимости | z | = 1 определяющего степенного ряда. (Соответствующее уравнение Jonquière (1889 , уравнение 5) и Erdélyi et al. (1981 , § 1.11-16) неверно, если предположить, что главные ветви полилогарифма и логарифма используются одновременно.) См. Следующее пункт для упрощенной формулы, когда s является целым числом.

• Для положительных целочисленных порядков полилогарифма s дзета-функция Гурвица ζ (1− s , x ) сводится к полиномам Бернулли , ζ (1− n , x ) = −B n ( x ) / n и формуле обращения Жанкьера для n = 1 , 2, 3, ... становится:

где снова 0 ≤ Re ( x ) <1, если Im ( x ) ≥ 0, и 0 x ) ≤ 1, если Im ( x ) <0. При ограничении аргумента полилогарифма единичным кругом Im ( x ) = 0, левая часть этой формулы упрощается до 2 Re (Li n ( e 2 πix )), если n четное, и до 2 i Im (Li n ( e 2 πix )), если n нечетное. Для отрицательных целочисленных порядков, с другой стороны, дивергенция Γ ( s ) подразумевает для всех z, что ( Erdélyi et al. 1981 , § 1.11-17):

В более общем случае для n = 0, ± 1, ± 2, ± 3, ...

где оба выражения совпадают для z ∉] 0; ∞ [. (Соответствующее уравнение Jonquière (1889 , уравнение 1) и Erdélyi и др. (1981 , § 1.11-18) снова неверно.)

• Полилогарифм с чисто мнимым µ может быть выражен через функции Клаузена Ci s (θ) и Si s (θ) и наоборот ( Левин 1958 , гл. VII § 1.4; Абрамовиц и Стегун 1972 , § 27.8):

• Арктангенс интеграл Ti сек ( г ) ( Левин 1958 . Ч. VII , § 1.2) может быть выражено в терминах полилогарифмов:

Отношение, в частности, подразумевает:

который объясняет имя функции.

• Функция Лежандра-чи χ s ( z ) ( Lewin 1958 , Ch. VII § 1.1; Boersma & Dempsey 1992 ) может быть выражена через полилогарифмы:

• Полилогарифм целочисленного порядка можно выразить как обобщенную гипергеометрическую функцию :

• В терминах неполных дзета-функций или « функций Дебая » ( Abramowitz & Stegun 1972 , § 27.1):

полилогарифм Li n ( z ) для положительного целого числа n можно выразить как конечную сумму ( Wood 1992 , § 16):

Замечательно похожее выражение связывает «функции Дебая» Z n ( z ) с полилогарифмом:

Применение полилогарифмов

• используется для приближенного решения неоднородного телеграфного уравнения для линии без искажений
• Полиномиальные решения краевых задач для уравнения Пуассона в слое
• и др

Вау!! 😲 Ты еще не читал? Это зря!

• Квантовый логарифм
• логарифм
• дилогарифм ,

На этом все! Теперь вы знаете все про полилогарифм, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое полилогарифм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)

Из статьи мы узнали кратко, но содержательно про полилогарифм