Вычет (комплексный анализ)

Привет, сегодня поговорим про вычет комплексный анализ , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое вычет комплексный анализ , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

В компле́ксном анализе вы́четом заданного объекта (функции, формы) называется объект (число, форма или когомологический класс формы), характеризующий локальные свойства заданного.

История[править ]

Теория вычетов одного комплексного переменного была в основном разработана О. Коши в 1825—1829 гг. Кроме него, важные и интересные результаты были получены Ш. Эрмитом, Ю. Сохоцким, Э. Линделефом и многими другими.

В 1887 году А. Пуанкаре обобщил интегральную теорему Коши и понятие вычета на случай двух переменных^[1], с этого момента и берет свое начало многомерная теория вычетов. Однако, оказалось, что обобщить это понятие можно различными способами.

Обозначение[править ]

Для обозначения вычета аналитической функции 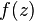 в точке  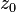применяется выражение 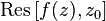, от англ. Residue. В некоторой литературе обозначается какВыч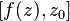^[2].

Одномерный комплексный анализ[править ]

Определение[править ]

Пусть 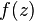 — комплекснозначная функция в области 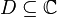, голоморфная в некоторой проколотой окрестности точки .

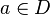Вычетом функции 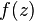 в точке  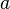называется число

.

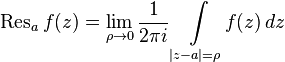В силу голоморфности функции 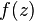 в малой проколотой окрестности точки  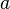по теореме Коши величина интеграла не зависит от  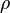при достаточно малых значениях этого параметра, так же как и от формы пути интегрирования. Важно только то, что путь является замкнутой кривой в области аналитичности функции, один раз охватывающей рассматриваемую точку и никаких других точек не принадлежащих области голоморфности .

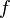В некоторой окрестности точки 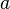 функция  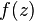представляется сходящимся рядом Лорана по степеням 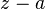. Нетрудно показать, что вычет совпадает с коэффициентом ряда  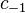при 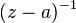. Об этом говорит сайт https://intellect.icu . Часто это представление принимают за определение вычета функции.

Вычет в «бесконечности»[править ]

Для возможности более полного изучения свойств функции вводится понятие вычета в бесконечности, при этом она рассматривается как функция на сфере Римана. Пусть бесконечно удаленная точка является изолированной особой точкой 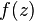, тогда вычетом в бесконечности называется комплексное число, равное

.

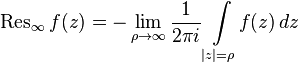Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.

Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удаленной точки:

.

Вычет дифференциальной формы[править ]

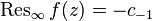С точки зрения анализа на многообразиях вводить специальное определение для некоторой выделенной точки сферы Римана (в данном случае, бесконечно удаленной) неестественно. Более того, такой подход затруднительно обобщить на более высокие размерности. Поэтому понятие вычета вводится не для функций, а для дифференциальных -форм на сфере Римана:

.

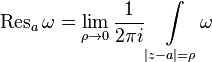На первый взгляд разницы в определениях никакой, однако теперь 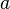 — произвольная точка 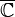, и смена знака при вычислении вычета в бесконечности достигается за счет замены переменных в интеграле.

Логарифмические вычеты[править ]

Интеграл 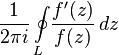 называется логарифмическим вычетом функции  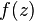относительно контура .

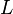Понятие логарифмического вычета используется для доказательства теоремы Руше и основной теоремы алгебры

Способы вычисления вычетов[править ]

Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоемко. Поэтому на практике пользуются, в основном, следствиями из определения:

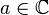• В устранимой особой точке , так же как и в точке регулярности, вычет функции  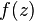равен нулю. В то же время для бесконечно удаленной точки это утверждение не верно. Например, функция  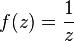имеет в бесконечности нуль первого порядка, однако, 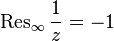. Причина этого в том, что форма 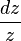имеет особенность как в нуле, так и в бесконечности.

• В полюсе  кратности  вычет может быть вычислен по формуле: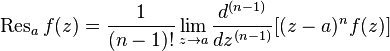

,

частный случай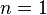 

.

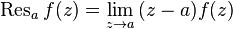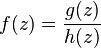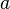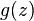• Если функция  имеет простой полюс в точке , где  и 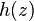 голоморфные в окрестности  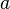функции, 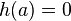, , 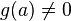то можно использовать более простую формулу:

.

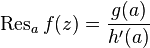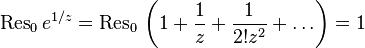• Очень часто, особенно в случае существенно особых точек, удобно вычислять вычет пользуясь разложением функции в ряд Лорана. Например, , так как коэффициент при  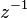равен 1.

Приложения теории вычетов[править ]

В большинстве случаев теория вычетов применяется для вычисления разного рода интегральных выражений с помощью основной теоремы о вычетах. Часто полезной в данных случаях бывает лемма Жордана.

Вычисления определенных интегралов от тригонометрических функций[править ]

Пусть функция 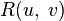 — рациональная функция переменных  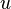и 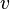. Для вычисления интегралов вида  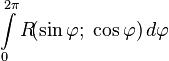удобно использовать формулы Эйлера. Положив, что 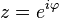, и произведя соответствующие преобразования, получим:

.

Вычисление несобственных интегралов[править ]

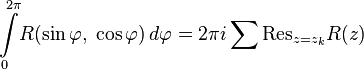Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:

1. Пусть функция 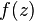 голоморфна в верхней полуплоскости  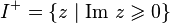и на вещественной оси за исключением конечного числа  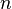полюсов, не лежащих на вещественной оси и 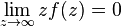. Тогда

.

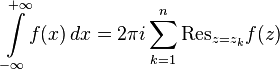2. Пусть функция 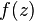 голоморфна в верхней полуплоскости  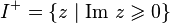и на вещественной оси за исключением конечного числа  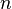полюсов, не лежащих на вещественной ос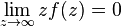и,  и 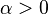. Тогда

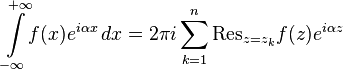
При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).

Многомерный комплексный анализ[править ]

Форма-вычет и класс-вычет[править ]

Этот раздел не завершен. Вы поможете проекту, исправив и дополнив его.

Локальный вычет[править ]

Этот раздел не завершен. Вы поможете проекту, исправив и дополнив его.

Вычетный поток[править ]

Этот раздел не завершен. Вы поможете проекту, исправив и дополнив его.

На этом все! Теперь вы знаете все про вычет комплексный анализ , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое вычет комплексный анализ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)