Гамма-функция

Привет, сегодня поговорим про гамма-функция, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое гамма-функция , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).

гамма-функция  — математическая функция, которая расширяет понятие факториала на поле комплексных чисел. Обычно обозначается .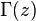

Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Определения[править ]

 

График гамма-функции действительного переменного

Интегральное определение[править ]

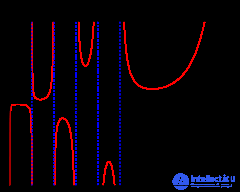
Если вещественная часть комплексного числа 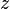 положительна, то Гамма-функция определяется через интеграл

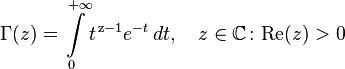
На всю комплексную плоскость функция аналитически продолжается через тождество

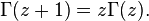
Существует непосредственное аналитическое call-with-current-continuation -8294#term-prodolzhenie">продолжение исходной формулы на всю комплексную плоскость , называемое интегралом Римана-Ханкеля

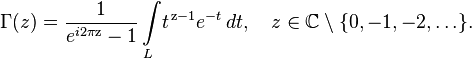
где контур 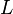 — любой контур на комплексной плоскости, обходящий точку  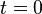против часовой стрелки, и концы которого уходят на бесконечность вдоль положительной вещественной оси.

Последующие выражения служат альтернативными определениями Гамма-функции.

Определение по Гауссу[править ]

Оно верно для всех комплексных 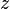, за исключением 0 и отрицательных целых чисел

Определение по Эйлеру[править ]

Определение по Вейерштрассу[править ]

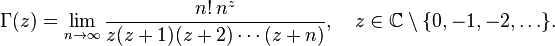
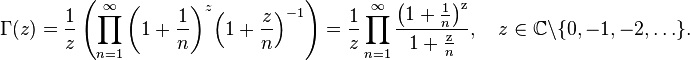
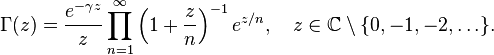
где 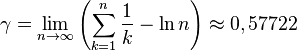 — постоянная Эйлера — Маскерони.

Замечания [править ]

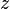• Интеграл выше сходится абсолютно, если вещественная часть комплексного числа   положительна.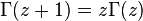
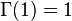• Применяя  интегрирование по частям , можно показать, что тождество

  

выполняется для подынтегрального выражения .

• А поскольку , для всех натуральных чисел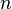 

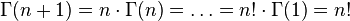
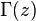•  является мероморфной на комплексной плоскости и имеющей полюса в точках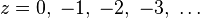 

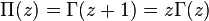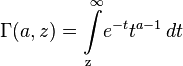
Связанные определения[править ]

• Иногда используется альтернативная запись, так называемая пи-функция, зависящая от гамма-функции следующим образом:

  .

• В интеграле выше, определяющем гамма-функцию, пределы интегрирования фиксированы. Об этом говорит сайт https://intellect.icu . Рассматривают также неполную гамма-функцию, определяемую аналогичным интегралом с переменным верхним либо нижним пределом интегрирования. Различают верхнюю неполную гамма-функцию, часто обозначаемую как гамма-функцию от двух аргументов:

и нижнюю неполную гамма-функцию, аналогично обозначаемую строчной буквой «гамма»:

.

Свойства[править ]

 

График модуля гамма-функции на комплексной плоскости .

• Формула дополнения Эйлера:

  .

• Из нее вытекает формула умножения Гаусса _en^ru:

  

• которую при n=2 называют формулой удвоения Лежандра:

  

• Наиболее известные значения гамма-функции от нецелого аргумента это

  

  

  

  

  

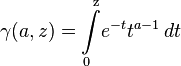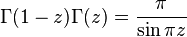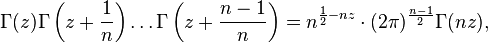
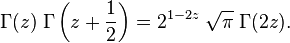
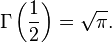
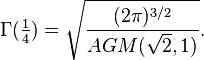
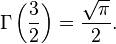
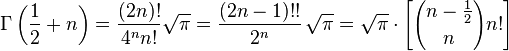
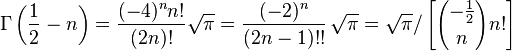
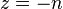• Гамма-функция имеет полюс в  для любого натурального  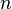и нуля; вычет в этой точке задается так

  .

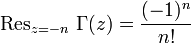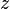• Следующее бесконечное произведение для гамма-функции, как показал Вейерштрасс, верно для всех комплексных , не являющихся неположительными целыми:

  ,

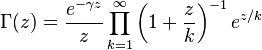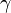где  — это константа Эйлера.

• Основное, но полезное свойство , которое может быть получено из предельного определения:

  .

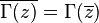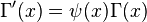• Гамма-функция дифференцируема бесконечное число раз, и , где 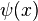 часто называют «пси-функцией», или дигамма-функцией.
• Гамма-функция и бета-функция связаны следующим соотношением:

  .

Литература[править ]

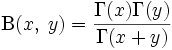Кузнецов Д.С. Специальные функции (1962) - 249 с.

Вау!! 😲 Ты еще не читал? Это зря![править ]

• Список объектов, названных в честь Леонарда Эйлера
• K-функция
• G-функция Барнса
• Бета-функция
• Гамма-распределение
• Неполная гамма- функция

На этом все! Теперь вы знаете все про гамма-функция, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое гамма-функция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)