Лекция
Привет, сегодня поговорим про голоморфная функция, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое голоморфная функция, регулярная функция, аналитическая функция, функция комплексного переменного , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
голоморфная функция , иногда называемая регулярной функцией —
функция комплексного переменного , определенная на открытом подмножестве комплексной плоскости 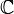 и комплексно дифференцируемая в каждой точке.
и комплексно дифференцируемая в каждой точке.
В отличие от вещественного случая, это условие означает, что функция бесконечно дифференцируема и может быть представлена сходящимся к ней рядом Тейлора.
Голоморфные функции также называют иногда аналитическими, хотя второе понятие гораздо более широкое, так как аналитическая функция не обязана быть определена на множестве комплексных чисел. Тот факт, что для комплекснозначных функций комплексной переменной множества голоморфных и аналитических функций совпадают, является нетривиальным и весьма замечательным результатом комплексного анализа.
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ (голоморфная функция) - функция f(z) комплексной переменной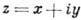 , к-рая дифференцируема в след. смысле: в каждой точке z0 нек-рой области D комплексной плоскости С существует производная
, к-рая дифференцируема в след. смысле: в каждой точке z0 нек-рой области D комплексной плоскости С существует производная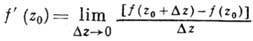 , причем предел не зависит от способа стремления Дг к нулю. Рассматриваются аналитическая функция. мн. комплексных переменных. аналитическая функция. широко распространены в математике и ее физ. приложениях. Ряд задач классич. веществ. анализа решается переходом к комплексным переменным. Все элементарные и спец. ф-ции аналитичны в тех или иных областях, причем выход в комплексную плоскость обнаруживает глубокие связи между этими ф-циями. Теория аналитическая функция прямо связана с теорией двумерного Лапласа уравнения и, следовательно, с теорией гармонических функций. Важной характеристикой аналитическая функция являются ее особенности, т. е. точки комплексной плоскости, в к-рых нарушается аналитичность.
, причем предел не зависит от способа стремления Дг к нулю. Рассматриваются аналитическая функция. мн. комплексных переменных. аналитическая функция. широко распространены в математике и ее физ. приложениях. Ряд задач классич. веществ. анализа решается переходом к комплексным переменным. Все элементарные и спец. ф-ции аналитичны в тех или иных областях, причем выход в комплексную плоскость обнаруживает глубокие связи между этими ф-циями. Теория аналитическая функция прямо связана с теорией двумерного Лапласа уравнения и, следовательно, с теорией гармонических функций. Важной характеристикой аналитическая функция являются ее особенности, т. е. точки комплексной плоскости, в к-рых нарушается аналитичность.
Классификация особенностей аналитическая функция позволяет во многом охарактеризовать и свойства ф-ции в целом. Ф-ции комплексной переменной использовались уже в 18 в., в частности в работах Л. Эйлера (L. Euler). Окончательно теория аналитическая функция. одной переменной оформилась в работах О. Коши (А. Саuchy), К. Вейерштрасса (К. Weierstrass) и Б.Римана (В. Riemann) в 19 в. Теория аналитическая функция. многих переменных продолжает интенсивно развиваться.
Одна из причин широкого применения аналитическая функция. в физике связана с физ. требованиями типа причинности. Так, в квантовой теории поля аналитичность Уайтмена функций и амплитуд рассеяния вытекает из исходных постулатов теории. Метод дисперсионных соотношений целиком базируется на теории аналитическая функция, ур-ния Янга - Миллса можно записать как условия аналитичности нек-рых ф-ций. Большое число приложений аналитическая функция связано также с двумерными задачами электростатики, гидродинамики и т. д., где используются, напр., конформные отображения.
Пусть 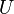 — открытое подмножество в
— открытое подмножество в 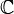 и
и 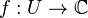 — комплекснозначная функция на
— комплекснозначная функция на 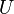 .
.
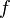 называют комплексно дифференцируемой в точке
называют комплексно дифференцируемой в точке 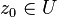 , если существует предел
, если существует предел
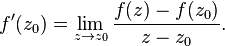
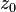 , для всех таких последовательностей выражение должно сходиться к одному и тому же числу
, для всех таких последовательностей выражение должно сходиться к одному и тому же числу 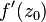 . Комплексное дифференцирование во многом похоже на вещественное: оно линейно и удовлетворяет тождеству Лейбница.
. Комплексное дифференцирование во многом похоже на вещественное: оно линейно и удовлетворяет тождеству Лейбница.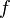 называют голоморфной в
называют голоморфной в 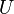 , если она комплексно дифференцируема в каждой точке
, если она комплексно дифференцируема в каждой точке 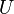 .
.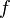 называют голоморфной в
называют голоморфной в 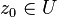 , если она голоморфна в некоторой окрестности
, если она голоморфна в некоторой окрестности 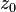 .
.Определению голоморфной функции можно придать несколько другой вид, если воспользоваться операторами 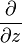 и
и 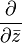 , определяемыми по правилу
, определяемыми по правилу
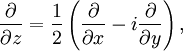
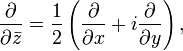
где 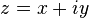 . Тогда функция
. Тогда функция 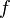 называется голоморфной, если
называется голоморфной, если
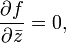
что эквивалентно условиям Коши — Римана.
Термин «голоморфная функция» был введен двумя учениками Коши, Брио (1817—1882) и Буке (1819—1895), и происходит от греческих слов őλoς (холос), что значит «целый», и μoρφń (морфе) — форма, образ.
Сегодня многие математики предпочитают термин «голоморфная функция» вместо «аналитическая функция», так как второе понятие более общее. Кроме того, одним из важных результатом комплексного анализа является то, что любая голоморфная функция является аналитической, что не очевидно из определения. Термин «аналитический» употребляют обычно для более общих функций, заданных не обязательно на комплексной плоскости.
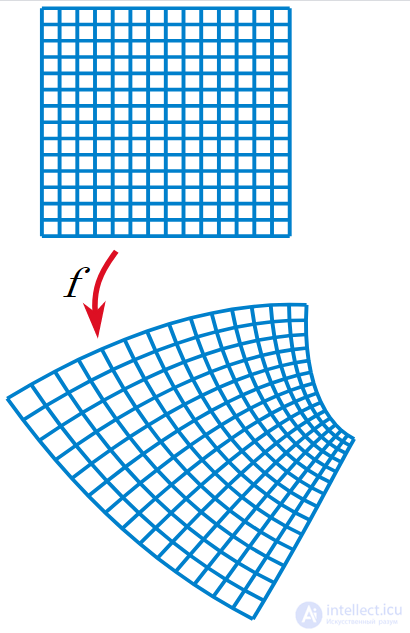
Голоморфная функция осуществляет конформное отображение, преобразуя ортогональную сетку в ортогональную (там где комплексная производная не обращается в нуль).
 и имеющая во всех своих особых точках
и имеющая во всех своих особых точках  полюс.
полюс. называется голоморфной на компакте
называется голоморфной на компакте  , если существует открытое множество
, если существует открытое множество  , содержащее
, содержащее 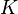 , такое что
, такое что 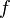 голоморфна в
голоморфна в  .
.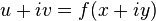 является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана
является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана

и частные производные 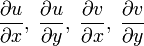 непрерывны.
непрерывны.
 . То есть если
. То есть если 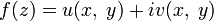 — голоморфная функция, то
— голоморфная функция, то 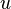 и
и 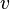 — гармонические функции.
— гармонические функции. равномерно сходится на любом компакте в
равномерно сходится на любом компакте в 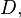 то его сумма также голоморфна, причем ее производная является пределом производных частичных сумм ряда .
то его сумма также голоморфна, причем ее производная является пределом производных частичных сумм ряда .Основные свойства. Если  и
и 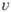 - вещественная и мнимая части ф-ции
- вещественная и мнимая части ф-ции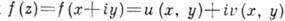 , то требование существования комплексной производной эквивалентно т. н. ур-ниям Коши - Римана
, то требование существования комплексной производной эквивалентно т. н. ур-ниям Коши - Римана

из к-рых следует, что 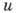 и
и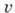 являются гармонич. ф-циями. Две ф-ции, гармонические в области D и удовлетворяющие там ур-ниям Коши - Римана, наз. взаимно сопряженными. Любая производная
являются гармонич. ф-циями. Две ф-ции, гармонические в области D и удовлетворяющие там ур-ниям Коши - Римана, наз. взаимно сопряженными. Любая производная 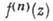 А. ф. f(z) есть также А. ф. В окрестности каждой точки z из области D А. ф. можно разложить в абсолютно сходящийся ряд Тейлора:
А. ф. f(z) есть также А. ф. В окрестности каждой точки z из области D А. ф. можно разложить в абсолютно сходящийся ряд Тейлора:
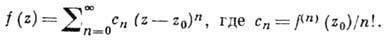
Радиус сходимости этого ряда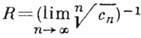 не меньше радиуса любого круга с центром в z0, содержащегося в D. Обратно, если в каждой точке z0 из D ф-ция f(z) представима абсолютно сходящимся степенным рядом, то f(z) аналитична в D, так что разложимость в степенной ряд можно считать др. эквивалентным определением А. ф.
не меньше радиуса любого круга с центром в z0, содержащегося в D. Обратно, если в каждой точке z0 из D ф-ция f(z) представима абсолютно сходящимся степенным рядом, то f(z) аналитична в D, так что разложимость в степенной ряд можно считать др. эквивалентным определением А. ф.
Пример: для распространенных элементарных ф-ций ez, sin z и cos z имеют место след. разложения в точке z0=0:
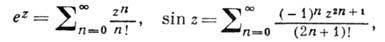

из к-рых, в частности, вытекает ф-ла Эйлера
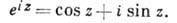
Специфичны и интегральные св-ва А. ф. Если замкнутый контур Y целиком лежит в области аналитичности D ф-ции / (z) и там его можно стянуть в точку, то интеграл от /(z) по этому контуру равен нулю. Это свойство также вполне характеризует А. ф.: если 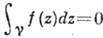 для нек-рой непрерывной в D ф-ции / (z) для любого контура
для нек-рой непрерывной в D ф-ции / (z) для любого контура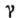 с перечисленными выше свойствами, то f(z) аналитична в D. Для А. ф. выполняется важная ф-ла Коши
с перечисленными выше свойствами, то f(z) аналитична в D. Для А. ф. выполняется важная ф-ла Коши
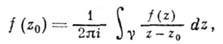
справедливая для любой точки z0, к-рая лежит в области, ограниченной контуром 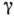 , причем направление обхода контура должно быть таким, чтобы область оставалась слева.
, причем направление обхода контура должно быть таким, чтобы область оставалась слева.
Для А. ф. имеет место принцип максимума модуля, согласно к-рому модуль А. ф., отличной от постоянной, не может достигать своего макс. значения ни в какой внутр. точке области аналитичности D. Напр., если А. ф. задана в единичном шаре 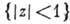 , по модулю не превосходит там 1 и f(0)=0, то
, по модулю не превосходит там 1 и f(0)=0, то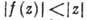 при
при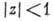 (лемма Шварца). Применительно к областям спец. вида принцип максимума приводит к следующей теореме Фрагмена - Линделефа.
(лемма Шварца). Применительно к областям спец. вида принцип максимума приводит к следующей теореме Фрагмена - Линделефа.
Пусть f(z) аналитична в секторе 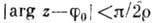 и непрерывна вплоть до его границы, на к-рой ее модуль не превосходит постоянной М. Если, кроме того,
и непрерывна вплоть до его границы, на к-рой ее модуль не превосходит постоянной М. Если, кроме того, 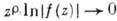 при
при 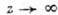 , то
, то 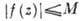 во всем секторе. Теоремы типа Фрагмена - Линделефа существенно используются в теории рассеяния элементарных частиц высокой энергии, приводя там к асимптотич. соотношениям между сечениями рассеяния частиц и античастиц (Померанчука теорема и др.).
во всем секторе. Теоремы типа Фрагмена - Линделефа существенно используются в теории рассеяния элементарных частиц высокой энергии, приводя там к асимптотич. соотношениям между сечениями рассеяния частиц и античастиц (Померанчука теорема и др.).
Понятие аналитичности имеет смысл также и на множествах более сложных, чем области комплексной плоскости С, но локально устроенных как последние. Напр., добавляя к С бесконечно удаленную точку, получают расширенную комплексную плоскость С. Комплексная структура в окрестности бесконечно удаленной точки задается отображением 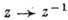 , переводящим ее в начало координат. Ф-ция f(z) аналитична в окрестности бесконечно удаленной точки, если
, переводящим ее в начало координат. Ф-ция f(z) аналитична в окрестности бесконечно удаленной точки, если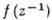 аналитична в окрестности точки z=0. Для областей в
аналитична в окрестности точки z=0. Для областей в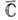 справедливо все сказанное выше. В то же время, если f(z) аналитична во всей
справедливо все сказанное выше. В то же время, если f(z) аналитична во всей 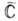 , то она постоянна (теорема Лиувилля).
, то она постоянна (теорема Лиувилля).
Особые точки. Точки, в к-рых нарушается аналитичность ф-ции f(z), наз. ее особыми точками. Если f(z) аналитична во всех точках нек-рой окрестности точки z0, кроме, быть может, ее самой, то z0 наз. изолиров. особой точкой. В окрестности изолиров. особой точки f(z) разлагается в абсолютно сходящийся ряд Лорана, содержащий, быть может, отрицат. степени (z-z0):
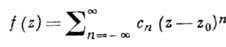
Различают три типа изолиров. особых точек: устранимую особую точку, полюс и существенно особую точку. Точка z0 наз. устранимой, если f(z) ограничена в нек-рой ее окрестности. Полагая 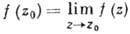 (этот предел существует), получают ф-цию, аналитическую и в z0. Изолиров. особая точка z0 наз. полюсом, если
(этот предел существует), получают ф-цию, аналитическую и в z0. Изолиров. особая точка z0 наз. полюсом, если 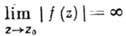 .
.
В этом случае лишь конечное число членов лорановского разложения f(z) в z0 с отрицат. степенями (z - z0) отлично от нуля. Коэф. c_j наз. вычетом функции f(z) в точке z0 и обозначается 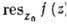 . Если бесконечное число членов ряда Лорана f (z) в точке z0 с отрицат. показателями п отлично от нуля, то z0 наз. существенно особой точкой. Существенно особые точки характеризуются тем, что для любого комплексного числа а существует последовательность zк, сходящаяся к z0 при
. Если бесконечное число членов ряда Лорана f (z) в точке z0 с отрицат. показателями п отлично от нуля, то z0 наз. существенно особой точкой. Существенно особые точки характеризуются тем, что для любого комплексного числа а существует последовательность zк, сходящаяся к z0 при  , такая, что
, такая, что 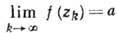
Пусть 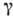 -замкнутый контур, лежащий в области аналитичности ф-ции f(z) и содержащий внутри себя лишь ее полюсы (их обязательно конечное число), расположенные в точках z1 ..., zn, тогда
-замкнутый контур, лежащий в области аналитичности ф-ции f(z) и содержащий внутри себя лишь ее полюсы (их обязательно конечное число), расположенные в точках z1 ..., zn, тогда
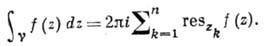
Эта формула является основой теории вычетов и служит эфф. инструментом для вычисления определ. интегралов. Ф-ция, аналитическая во всей комплексной плоскости, за исключением, быть может, полюсов, наз. мероморфной. Ф-ция, не имеющая в С особых точек, наз. целой.
Многозначные функции. Всякая А. ф. однозначно восстанавливается по своим значениям в любом сколь угодно малом открытом подмножестве области аналитичности. Более того, если две аналитические в D ф-ции совпадают в счетном числе точек из D, имеющих хотя бы одну предельную точку, также принадлежащую D, то эти ф-ции совпадают и всюду в D. Типичной является ситуация, когда А. ф. первоначально задана в нек-рой области D, но продолжается до А. ф. в существенно большей области. Т. о., возникает задача об аналитическом продолжении заданной А. ф. до А. ф. в максимально возможной области.
Чтобы эта задача была разрешима в классе однозначных ф-ций, приходится расширить понятие области, допустив возможность ее самоналожений. Это приводит к понятию неоднолистных областей, в частности римановой поверхности данной А. ф. Пусть f(z) - А. ф. в области D к  - нек-рый путь, соединяющий точку z0 из D с точкой z' из расширенной комплексной плоскости. Говорят, что f(z) аналитически продолжается вдоль
- нек-рый путь, соединяющий точку z0 из D с точкой z' из расширенной комплексной плоскости. Говорят, что f(z) аналитически продолжается вдоль , если существует конечное число кругов Vк, к=0, 1, ..., N с центрами, последовательно расположенными на
, если существует конечное число кругов Vк, к=0, 1, ..., N с центрами, последовательно расположенными на 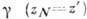 , и ф-ции fк(z) аналитические в Vк, такие, что fк(z)= =fк-1(z) в пересечении Vк, и Vk-1.
, и ф-ции fк(z) аналитические в Vк, такие, что fк(z)= =fк-1(z) в пересечении Vк, и Vk-1.
Если f(z) аналитически продолжается вдоль двух путей 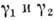 с началом в z0 и концом в z', то в результате этих продолжений в окрестности точки z' могут получиться, вообще говоря, разные А. ф. Риманову поверхность ф-ции f(z), первоначально заданной в D, можно понимать как множество всех путей, к рые исходят из нек-рой точки z0, лежащей в D, и вдоль к-рых f(z) аналитически продолжима. При этом два пути отождествляются, если они заканчиваются в одной и той же точке и приводят к одинаковым А. ф. в ее окрестности. Тем самым всякая аналитическая в D ф-ция f(z) определяет нек-рую ф-цию, аналитическую на своей римановой поверхности,- полную А. ф.
с началом в z0 и концом в z', то в результате этих продолжений в окрестности точки z' могут получиться, вообще говоря, разные А. ф. Риманову поверхность ф-ции f(z), первоначально заданной в D, можно понимать как множество всех путей, к рые исходят из нек-рой точки z0, лежащей в D, и вдоль к-рых f(z) аналитически продолжима. При этом два пути отождествляются, если они заканчиваются в одной и той же точке и приводят к одинаковым А. ф. в ее окрестности. Тем самым всякая аналитическая в D ф-ция f(z) определяет нек-рую ф-цию, аналитическую на своей римановой поверхности,- полную А. ф.
Пусть f(z) аналитична в нек-рой области D и аналитически продолжается (вообще говоря, неоднозначно) вдоль любого пути, не содержащего фиксиров. точку z0 (такая точка наз. точкой ветвления). Если провести разрез плоскости С, соединяющий точку z0 с бесконечно удаленной точкой, то можно получить конечное или счетное число ф-ций, аналитичных в плоскости С с разрезом, получающихся из f(z) аналитич. продолжением вдоль путей, огибающих z0 заданное число раз. Риманову поверхность ф-ции f(z) можно представить себе как конечное или счетное число экземпляров плоскостей С с разрезом (листов), склеенных вдоль берегов разрезов таким образом, что каждый оборот вокруг z0 переводит точку на новый лист.
А. ф., заданная в области D, наз. однолистной в D, если она осуществляет взаимно однозначное отображение D на ее образ 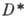 =f(D), к-рый также является областью. Всякая однолистная в D А. ф. задает конформное отображение D на
=f(D), к-рый также является областью. Всякая однолистная в D А. ф. задает конформное отображение D на  в том смысле, что оно сохраняет углы между кривыми. Обратно, всякое (гладкое) конформное взаимно однозначное отображение D на
в том смысле, что оно сохраняет углы между кривыми. Обратно, всякое (гладкое) конформное взаимно однозначное отображение D на 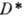 , сохраняющее углы между кривыми (по величине и знаку), порождается нек-рой однолистной в D А. ф., такой, что
, сохраняющее углы между кривыми (по величине и знаку), порождается нек-рой однолистной в D А. ф., такой, что 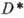 =f(D). Области D и
=f(D). Области D и в этом случае наз. конформно изоморфными. Согласно теореме Римана, любые две односвязные области, границы которых состоят более чем из одной точки, конформно изоморфны.
в этом случае наз. конформно изоморфными. Согласно теореме Римана, любые две односвязные области, границы которых состоят более чем из одной точки, конформно изоморфны.
Функции многих переменных. Теория А. ф. мн. комплексных переменных по сравнению с одномерной теорией обладает новыми специфич. чертами. Ф-ция f(z), z=(z1, ..., zn) наз. аналитической (голоморфной) в области D n-мерного комплексного пространства 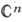 , если в окрестности каждой ее точки z0=(z01, ..., z0n) она представляется в виде суммы абсолютно сходящегося степенного ряда:
, если в окрестности каждой ее точки z0=(z01, ..., z0n) она представляется в виде суммы абсолютно сходящегося степенного ряда:
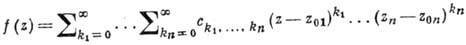
По теореме Гартогса f(z) аналитична в D тогда и только тогда, когда она аналитична по каждому переменному в отдельности при фиксированных остальных в соответствующих сечениях области D.
Важное отличие многомерной теории от одномерной состоит в существовании таких областей, что голоморфные в них ф-ции обязательно аналитически продолжаются в существенно большие области. В частности, при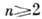 не существует А. ф. с изолиров. особенностями. Естеств. областями определения А. ф. служат т. н. области голоморфности. Область D в
не существует А. ф. с изолиров. особенностями. Естеств. областями определения А. ф. служат т. н. области голоморфности. Область D в 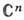 наз. областью голоморфности, если существует ф-ция, голоморфная в D и аналитически непродолжимая ни в какую другую большую область (в т. ч. и неоднолистную).
наз. областью голоморфности, если существует ф-ция, голоморфная в D и аналитически непродолжимая ни в какую другую большую область (в т. ч. и неоднолистную).
Свойство области быть областью голоморфности есть локальное свойство ее границы, обобщающее понятие выпуклости. Если D не является областью голоморфности, то все ф-ции, голоморфные в D, одноврем. продолжаются в нек-рую большую область. Вопрос об отыскании такой наибольшей области (оболочки голоморфности), как и в случае аналитич. продолжения заданной функции, приводит к многолистным областям наложения над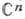 (многообразиям Штейна).
(многообразиям Штейна).
Др. пример неожиданного "принудительного" продолжения многомерных А. ф. дает теорема об острие клина (получена Н. Н. Боголюбовым в 1956), играющая важную роль в теории дисперсионных соотношений и аксиоматич. квантовой теории поля. По этой теореме две ф-ции, аналитические каждая в своей спец. вида трубчатой области и совпадающие на n-мерном чисто вещественном открытом множестве соприкосновения этих областей (т. е. на множестве вдвое меньшей размерности), аналитически продолжаются в комплексную окрестность G этого множества и представляют собой единую А. ф. Вид области G можно найти с помощью теоремы о С-выпуклой оболочке (получена В. С. Владимировым в 1964).
Существует также определение голоморфности функций многих комплексных переменных
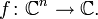
Для определения используются понятия 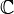 -дифференцируемости и
-дифференцируемости и 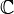 -линейности таких функций
-линейности таких функций
С-линейность[править ]
Функция 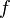 называется
называется 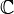 -линейной если удовлетворяются условия:
-линейной если удовлетворяются условия:
 .
.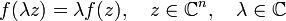
(для 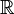 -линейных функций
-линейных функций 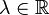 ).
).
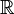 -линейной функции
-линейной функции 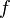 существуют последовательности
существуют последовательности 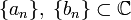 , такие, что
, такие, что 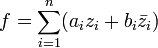 .
. -линейной функции
-линейной функции 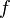 существуют последовательность
существуют последовательность  , такая, что
, такая, что 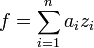 .
.С-дифференцируемость[править ]
Функция 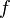 называется
называется  -дифференцируемой в точке
-дифференцируемой в точке 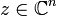 если существуют функции
если существуют функции 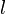 и
и  , такие что в окрестности точки
, такие что в окрестности точки 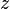
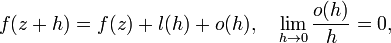
где 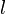 —
— 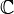 -линейная (для
-линейная (для 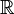 -дифференцируемости —
-дифференцируемости — 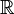 -линейная) функция.
-линейная) функция.
Голоморфность[править ]
Функция 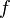 называется голоморфной в области
называется голоморфной в области 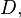 если она
если она 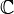 -дифференцируема в окрестности каждой точки этой области.
-дифференцируема в окрестности каждой точки этой области.
Все полиномиальные функции от z с комплексными коэффициентами голоморфны на C , как и синус , косинус и экспоненциальная функция . (Тригонометрические функции на самом деле тесно связаны с экспоненциальной функцией и могут быть определены с помощью формулы Эйлера ). Главная ветвь функции комплексного логарифма голоморфна на множестве C ∖ { z ∈ R : z ≤ 0}. Функция квадратного корня может быть определена как
и поэтому голоморфен везде, где стоит логарифм log ( z ). Функция 1 / z голоморфна на { z : z ≠ 0}.
Как следствие уравнений Коши – Римана , вещественнозначная голоморфная функция должна быть постоянной. Таким образом, абсолютное значение г , то аргумент о г , то действительная часть из г и мнимая часть из г не голоморфны. Другой типичный пример непрерывной функции, которая не является голоморфной, - комплексно сопряженная функция z, образованная комплексным сопряжением .
На этом все! Теперь вы знаете все про голоморфная функция, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое голоморфная функция, регулярная функция, аналитическая функция, функция комплексного переменного и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Комментарии
Оставить комментарий
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)
Термины: Комплексный анализ и операционное исчисление (теория функций комплексного переменного)