Сразу хочу сказать, что здесь никакой воды про неопределенный интеграл, и только нужная информация. Для того чтобы лучше понимать что такое неопределенный интеграл, первообразная , настоятельно рекомендую прочитать все из категории Математический анализ. Интегральное исчисление.

неопределенный интеграл . Понятие первообразной, основные понятия и определения

Определение

Первообрзная (иногда называемая антипроизводной или примити́вной функцией) — одно из важнейших понятий математического анализа вещественной переменной (существуют также обобщения этого понятия для комплексных функций).

Функция 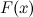называется первообразной для функции 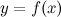на промежутке 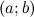, конечном или бесконечном, если функция 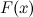дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:

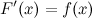
Последнее равенство можно записать через дифференциалы:

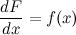или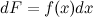

Первообразной для данной функции называют такую функцию , производная которой равна (на всей области определения ), то есть . Нахождение первообразной является операцией, обратной дифференцированию — последнее по заданной функции находит ее производную, а найдя первообразную, мы, наоборот, по заданной производной определили исходную функцию.

Первообразные важны тем, что позволяют вычислять определенные интегралы. Если — первообразная интегрируемой непрерывной функции , то:

Это соотношение называется формулой Ньютона — Лейбница.

Технически нахождение первообразной заключается в вычислении неопределенного интеграла для , а сам процесс называется интегрированием. О применении этой теории в геометрии см. Интегральное исчисление.

Пример: функция является первообразной для потому что

Пример

Функция 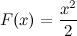является первообразной для функции 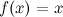, так как

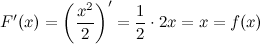
Первообразная 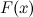имеет конечную производную, а, следовательно, является непрерывной функцией.

Теорема

(О бесконечном множестве первообразных для функции)

Если функция 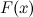является первообразной для функции 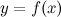на некотором промежутке, то и функция 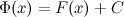, где 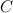- произвольная постоянная, также будет первообразной для функции 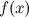на рассматриваемом промежутке.

Пример

Известно, что для функции 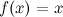первообразной является функция 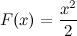, а, следовательно, и все функции вида 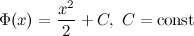также будут первообразными, так как выполняется равенство :

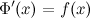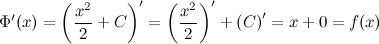
Таким образом, если функция 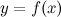имеет первообразную, то она имеет бесконечное множество первообразных.

Теорема

(Об общем виде первообразной для функции)

Если функци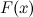и и 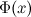- две любые первообразные функции 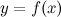, то их разность равна некоторой постоянной, то есть

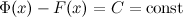
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции 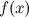, может быть представлена в виде .

Свойства первообразной

• Первообразная суммы равна сумме первообразных.
• Первообразная произведения константы и функции равна произведению константы и первообразной функции.
• У всех функций, непрерывных на отрезке, существуют и первообразная, и интеграл по Риману. Однако в общем случае существование первообразной и интегрируемость функции не связаны :
  • Функция знака (sgn) интегрируема по Риману, но не имеет первообразной (из-за разрыва в нуле).
  • У функции (положим также ) на отрезке имеется конечная производная таким образом, у функции существует первообразная (а именно, ), но не ограничена на и поэтому не интегрируема по Риману.

Неопределенный интеграл

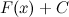Определение

Совокупность всех первообразных функции 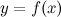, определенных на заданном промежутке, называется неопределенным интегралом от функции 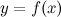и обозначается символом 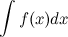. Об этом говорит сайт https://intellect.icu . То есть

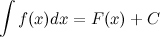
Знак 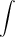называется интегралом, 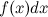- подынтегральным выражением, 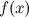- подынтегральной функцией, а - переменной интегрирования.

Операция нахождения первообразной или неопределенного интеграла от функции 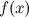называется интегрированием функции 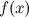. Интегрирование представляет собой операцию, обратную дифференцированию.

Геометрическая интерпретация неопределенного интеграла

Неопределенный интеграл представляет собой семейство параллельно расположенных кривых 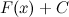, где каждому конкретному числовому значению постоянной 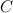соответствует определенная кривая из указанного семейства.

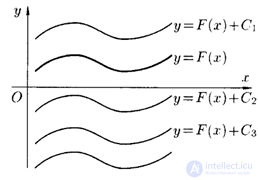
График каждой кривой из семейства называется интегральной кривой.

Теорема

Каждая непрерывная на промежутке 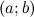функция, имеет на этом интервале первообразную.

Свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению

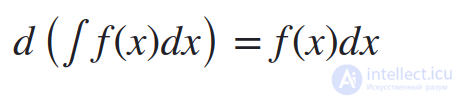
Пример

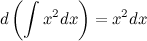
2. Производная от неопределенного интеграла равна подынтегральной функции

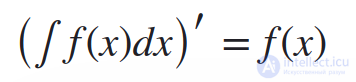
Пример

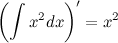
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

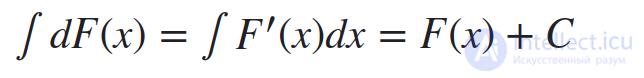
Пример

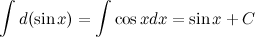
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла

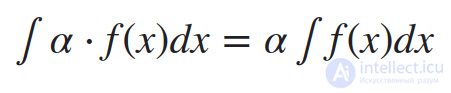
Пример

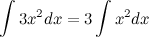
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций

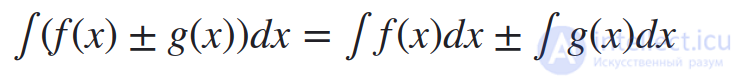
Пример

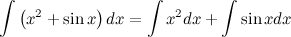
6. Если 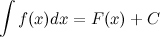, то и 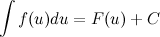, где функция 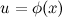- произвольная функция с непрерывной производной.

Пример

Известно, что 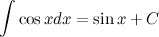, а тогда

Техника интегрирования Методы интегрирования Список интегралов элементарных функций

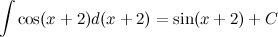
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

• линейность интегрирования позволяет разбивать сложные интегралы на части,
• интегрирование подстановкой, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
• интегрирование по частям для операций с произведениями функций,
• метод обратной цепочки, особый случай интегрирования по частям,
• метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
• алгоритм Риша - алгоритм для интегрирования любых элементарных функций,
• некоторые интегралы можно найти в таблице интегралов,
• при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
• Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведенные символьные операции (в частности алгоритм Риша), что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
• если функция не имеет элементарной первообразной (как, например, ), ее интеграл может быть вычислен приближенно с помощью численного интегрирования.

Таблица интегралов, таблица неопределенных интегралов

В таблице интегралов мы постарались собрать самое полное собрание формул, которое поможет Вам решить любой интеграл. Неизменными спутниками таблицы интегралов являются - таблица производных и формулы производных , которые также в полном виде представлена у нас на сайте.

Основные формулы

Методы решения неопределенных интегралов

1. Метод непосредственного интегрирования

Приведение к табличному виду или метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов.

Пример

Задание. Найти интеграл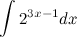

Решение. Воспользуемся свойствами интеграла и приведем данный интеграл к табличному виду.

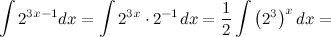
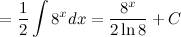
Ответ.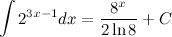

Метод непосредственного интегрирования

Определение

Метод интегрирования, при котором интеграл с помощью тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

Таким образом, алгоритм действий следующий:

1. тождественное преобразование подынтегральной функции;
2. применение свойств неопределенного интеграла: вынесение константы за знак интеграла, представление интеграла от суммы функций в вид суммы интегралов;
3. использование таблицы интегралов.

В простейших примерах для применения непосредственного интегрирования достаточно разложить подынтегральную функцию на слагаемые и постоянные величины вынести за знак интеграла.

При определенной практике интегрирования обычно эти действия проводят устно, записывая лишь результат интегрирования.

2. Внесение под знак дифференциала

В формуле неопределенного интеграла величина 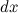означает, что берется дифференциал от переменной . Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула

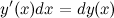
Если нужная функция 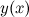отсутствует, иногда ее можно образовать путем алгебраических преобразований.

Интегрирование внесением под дифференциал

Пусть требуется найти неопределенный интеграл 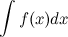. Предположим, что существуют дифференцируемые функци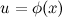и и 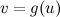такие, что

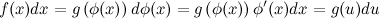
Тогда

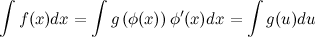
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.

Тогда, есл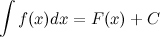и и 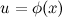, то имеет место следующее равенство:

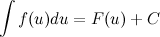
Замечание. При интегрировании методом подведения под знак дифференциала полезны следующие равенства для дифференциалов:

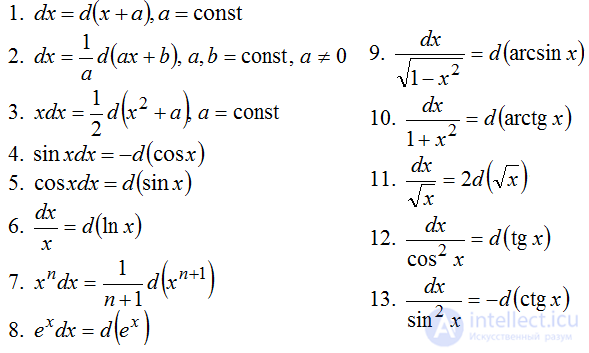
Пример

Задание. Внесением под дифференциал найти неопределенный интеграл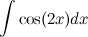

Решение. Внесем 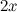под знак дифференциала, тем самым приведя исходный интеграл к табличному.

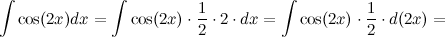
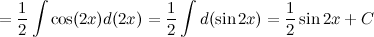
Ответ.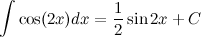

В общем виде справедливо равенство:

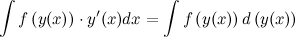
Пример

Задание. Найти интеграл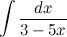

Решение. Внесем 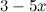под знак дифференциала, тем самым приведя исходный интеграл к табличному.

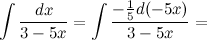
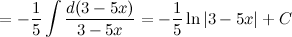
Ответ.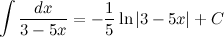

3. Интегрирование заменой переменной

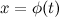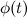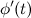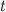Интегрирование заменой переменной или методом подстановки. Пусть , где функция имеет непрерывную производную , а между переменными и существует взаимно однозначное соответствие. Тогда справедливо равенство

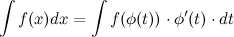
Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования.

Интегрирование заменой переменной

Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже самое, делается подстановка. После этого заданный в условии интеграл сводится либо к табличному интегралу, либо к нему сводящемуся.

Если в неопределенном интеграле 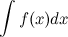сделать подстановку 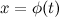, где функция 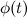- функция с непрерывной первой производной, то тогда 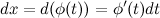и согласно свойству 6 неопределенного интеграла имеем, что:

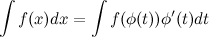
Эта формула называется формулой замены переменной в неопределенном интеграле.

Замечание

После нахождения интеграла по новой переменной 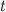необходимо вернуться к первоначальной переменной .

Замечание

В некоторых случаях целесообразно делать подстановку 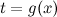, тогда

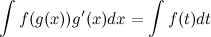
Пример

Задание. Найти интеграл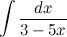

Решение. Заменим знаменатель на переменную 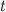и приведем исходный интеграл к табличному.

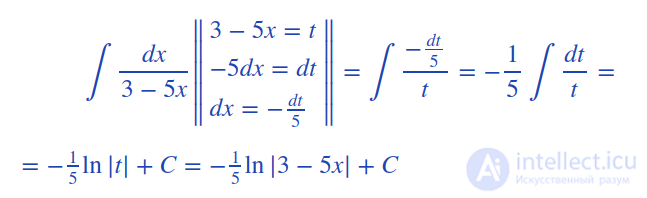
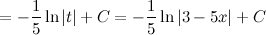
Ответ.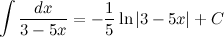

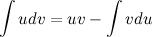
4 Интегрированием по частям называют интегрирование по формуле

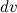При нахождении функции по ее дифференциалу можно брать любое значение постоянной интегрирования 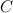, так как она в конечный результат не входит. Поэтому для удобства будем брать .

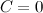Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой.

Метод интегрирования по частям

Рассмотрим функци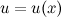и и 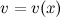, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство:

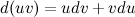
Проинтегрировав левую и правую части последнего равенства, получим:

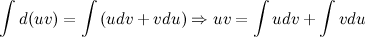
Полученное равенство перепишем в виде:

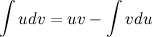
Эта формула называется формулой интегрирования по частям. С ее помощью интеграл 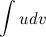можно свести к нахождению интеграла 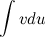, который может быть более простым.

Пример

Задание. Найти интеграл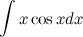

Решение. В исходном интеграле выделим функции и , затем выполним интегрирование по частям.

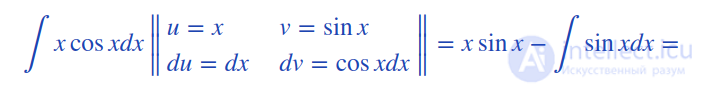
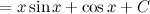
Ответ.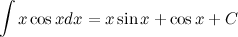

Вау!! 😲 Ты еще не читал? Это зря!

• Производная
• Дифференциал
• Интеграл

А как ты думаешь, при улучшении неопределенный интеграл, будет лучше нам? Надеюсь, что теперь ты понял что такое неопределенный интеграл, первообразная и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Интегральное исчисление