Лекция
Сразу хочу сказать, что здесь никакой воды про производная, и только нужная информация. Для того чтобы лучше понимать что такое производная, таблица производных, приложения производных, применение производных, физическое приложение производной , геометрическое приложение производной , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Пусть 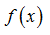 определена в точке
определена в точке 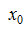 и в некоторой ее окрестности.
и в некоторой ее окрестности.
Пусть 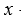 точка рассматриваемой окрестности, то приращением аргумента в точке
точка рассматриваемой окрестности, то приращением аргумента в точке 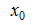 называется величина
называется величина 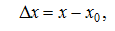 , приращением функции – величина
, приращением функции – величина  . Если выразить
. Если выразить 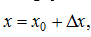 , то
, то  .
.
Производной функции 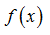 в точке
в точке 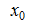 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
Производную в точке обозначают 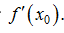 . По определению
. По определению
 , (1)
, (1)
или, что то же,
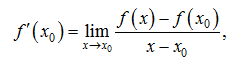 , (2)
, (2)
при условии, что пределы (1),(2) существуют.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
производная функции в точке – это число. Если функция дифференцируема на некотором множестве X из ее области определения, то 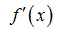 также является функцией (ее обозначают также
также является функцией (ее обозначают также 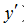 ).
).
Пусть 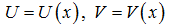 -дифференцируемые функции. Справедливы формулы:
-дифференцируемые функции. Справедливы формулы:
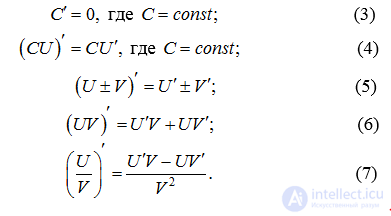
Если 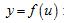 и
и 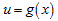 – дифференцируемые функции своих аргументов, то производная сложной функции
– дифференцируемые функции своих аргументов, то производная сложной функции 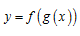
вычисляется по формуле 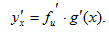

производная от синуса, косинуса, тангенса, артангенса, логорифма, константы
Пример



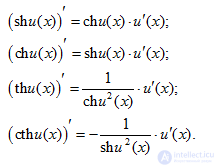
Если для функции 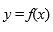 существует обратная функция
существует обратная функция 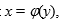 ,
,
которая имеет производную 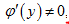 то верна формула
то верна формула 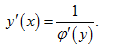
Уравнение касательной и нормали
Производная функции 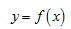 в точке
в точке 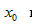 представляет собой угловой коэффициент касательной, проведенной к графику функции в точке
представляет собой угловой коэффициент касательной, проведенной к графику функции в точке
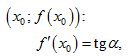
где 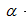 – угол наклона касательной к оси Ox. В этом состоит геометрический смысл производной.
– угол наклона касательной к оси Ox. В этом состоит геометрический смысл производной.
Уравнение касательной, проведенной к графику функции в точке 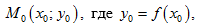 имеет вид:
имеет вид:
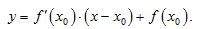 (11.9)
(11.9)
Прямая, проходящая через точку 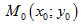 графика функции
графика функции 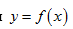 перпендикулярно касательной, проведенной в этой точке,
перпендикулярно касательной, проведенной в этой точке,
называется нормалью к графику функции 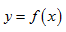 в точке
в точке 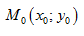 (рис. 11.1).
(рис. 11.1).
Уравнение нормали имеет вид:
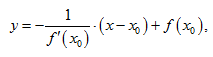 (11.10)
(11.10)
где 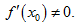
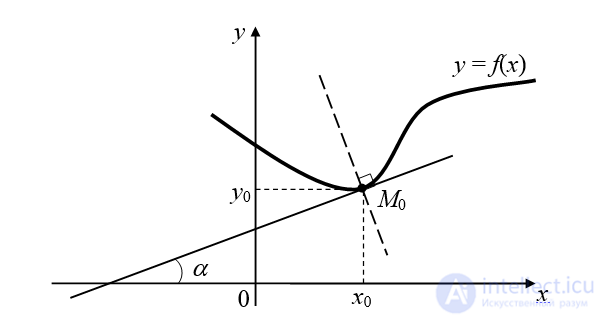
Рис. 11.1
1. КИНЕМАТИКА Если материальная точка M движется неравномерно по пути, заданному функцией 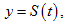 то мгновенная скорость движения в момент времени
то мгновенная скорость движения в момент времени 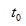 есть производная от пути S по времени t:
есть производная от пути S по времени t: 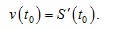 (11.11)
(11.11)
2.КИНЕМАТИКА Если функцией  описывается процесс изменения скорости неравномерного движения в зависимости от времени, то мгновенное ускорение материальной точки в момент времени
описывается процесс изменения скорости неравномерного движения в зависимости от времени, то мгновенное ускорение материальной точки в момент времени 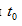 есть производная от скорости v по времени t:
есть производная от скорости v по времени t: 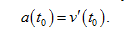 (11.12)
(11.12)
3.ТЕРМОДИНАМИКА Если 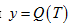 – функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры T, то теплоемкость тела есть производная от количества теплоты Q по температуре T:
– функция, описывающая процесс изменения количества теплоты, сообщаемой телу при нагревании его до температуры T, то теплоемкость тела есть производная от количества теплоты Q по температуре T: 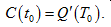
4. МАТЕРИАЛОВЕДЕНИЕ Линейная плотность неоднородного тонкого стержня в точке 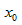 есть производная от массы m по длине l:
есть производная от массы m по длине l: 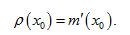
5. ЭЛЕКТРОДИНАМИКА Мгновенное значение электродвижущей силы индукции равно скорости изменения магнитного потока ,
т. е. производной от магнитного потока 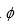 по времени t:
по времени t: 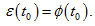
6. Об этом говорит сайт https://intellect.icu . Сила тока в колебательном контуре в момент времени 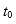 равна производной заряда q по времени t:
равна производной заряда q по времени t: 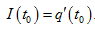
7. Максимальная мощность тока.
Мощность тока 
Известно, что функция имеет экстремум (max или min) в точке в которой ее производная равна нулю. В данном случае

Из решения полученного уравнения следует, что максимальная мощность при нагрузке может быть достигнута, если ее сопротивление R равно внутреннему
сопротивлению источника тока r. Т.е.
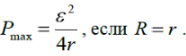
8.Мгновенное значение силы переменного тока
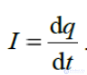 Например, при электромагнитных колебаниях, возникающих в колебательном контуре заряд на обкладках конденсатора изменяется
Например, при электромагнитных колебаниях, возникающих в колебательном контуре заряд на обкладках конденсатора изменяется
по закону 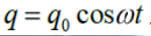
тогда 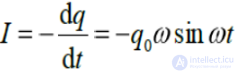
Пример 1. Написать уравнение касательной и нормали, проведенной к графику функции 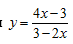 в точке с абсциссой x = 2.
в точке с абсциссой x = 2.
Решение.Для нахождения уравнения касательной воспользуемся формулой (9). Сначала найдем ординату точки касания 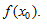
. Для этого значение x=2 подставим в уравнение функции:
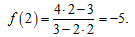
Для нахождения углового коэффициента найдем производную 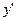 , используя формулу дифференцирования дроби:
, используя формулу дифференцирования дроби:

Найдем значение производной при x=2 :
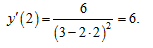
Подставляем найденные значения в формулу (9), получаем уравнение касательной:
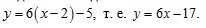
Чтобы написать уравнение нормали, воспользуемся формулой (10):

Получим, что уравнение нормали , проведенной к заданной кривой в заданной точке имеет вид 
Пример 2. Определить, в какой точке кривой 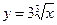 касательная наклонена к оси абсцисс под углом 45°.
касательная наклонена к оси абсцисс под углом 45°.
Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдем производную функции:
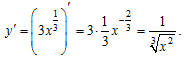 .
.
По условию 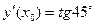 Значит,
Значит, 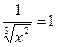 .
.
Отсюда
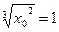 ,
, 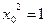 ,
, 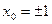 .
.
Получили два значения абсциссы точки касания:
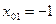 ,
, 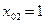 ,
,
т.е. существует две точки касания, в которых касательная образует угол  с осью
с осью 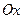 .
.
Найдем соответствующие ординаты точек касания, подставляя значения 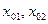 в формулу функции:
в формулу функции:
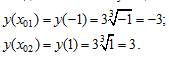
Приходим к ответу: в точках  и
и 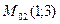 касательная к заданной кривой образует с осью
касательная к заданной кривой образует с осью 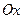 угол
угол 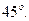
Пример 3. Найти острый угол между параболами 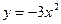 и
и 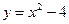 в точке их пересечения, имеющей отрицательную абсциссу.
в точке их пересечения, имеющей отрицательную абсциссу.
Решение. Угол между двумя кривыми в точке их пересечения - это угол между касательными к этим кривым, проведенными в точке их пересечения. Тангенс этого угла вычислим по формуле:
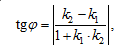 (13)
(13)
где 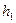 и
и 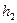 -угловые коэффициенты заданных парабол.
-угловые коэффициенты заданных парабол.
Найдем точку пересечения этих парабол. Для этого решим систему:

Отсюда 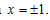 Условие задачи удовлетворяет точка
Условие задачи удовлетворяет точка  Найдем коэффициент
Найдем коэффициент 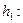
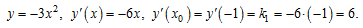 Аналогично найдем
Аналогично найдем 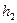 :
:
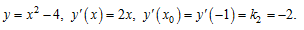
Воспользуемся формулой и получим:
 ,
,
откуда 
Пример 4. Тело движется прямолинейно по закону 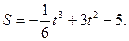 Найти скорость движения тела в тот момент, когда ускорение равно нулю.
Найти скорость движения тела в тот момент, когда ускорение равно нулю.
Решение. Согласно формуле (11) скорость есть производная пути, а, согласно формуле (12), ускорение есть производная от скорости.
Последовательно вычислим производные:

Найдем момент времени, когда ускорение равно нулю:

Вычислим скорость движения тела в момент времени 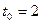
пример задачи физика- теплота
Вычислить количество теплоты, которое необходимо для того, чтобы нагреть 1 кг вещества от 0 градусов до t градусов (по Цельсию).
решение
Пусть Q=Q(t). Рассмотрим малый отрезок [t; t+Δt], на этом отрезке
ΔQ=c(t) • Δt
c(t)= ΔQ/Δt
При Δt→0 lim ΔQ/Δt =Q′(t)
Δt→0
c(t)=Q′(t)
Математическое моделирование применимо в различных областях знаний, поэтому и производную можно использовать не только в математике и смежных с ней дисциплинах
Доказательство неравенств
Решение уравнений
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)
Скоростью химической реакции в химии называется изменение концентрации реагирующих веществ в единицу времени или производная от концентрации реагирующих веществ по времени (на языке математике концентрация была бы функцией, а время –аргументом)
|
Понятие на языке химии |
Обозначение |
Понятие на языке математики |
|
Количество в-ва в момент времени t0 |
p = p(t 0) |
Функция |
|
Интервал времени |
∆t = t– t0 |
Приращение аргумента |
|
Изменение количества в-ва |
∆p= p(t0+ ∆ t ) – p(t0) |
Приращение функции |
|
Средняя скорость химической реакции |
∆p/∆t |
Отношение приращения функции к приращению аргумента |
|
скорость v(t) химической Если P(t) – закон изменения количества |
V (t) = p ‘(t) |
пример
Пусть количество вещества,вступившего в химическую реакцию задается зависимостью: р(t) = t2/2 + 3t –3 (моль)
Найти скорость химической реакции через 3 секунды.
решение
р(t) = t2/2 + 3t –3 (моль)
1. Найдем производную функции: Р’(t) = t +3
2. Подставим значение t = 3 сек: P’(3) = 3 + 3 = 6 (моль/сек )
Ответ: 6 (моль/сек )
Популяция – это совокупность особей данного вида, занимающих определенный участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

|
понятия на языке биологии |
Обозначение |
Понятие на языке математики |
|
Численность в момент времени t1 |
x = x(t) |
Функция |
|
Интервал времени |
∆t = t2 – t1 |
Приращение аргумента |
|
Изменение численности популяции |
∆x = x(t2) – x(t1)
|
Приращение функции |
| Скорость изменения численности популяции
|
Р = х‘ (t) =∆x/∆t |
Отношение приращения функции к приращению аргумента |
|
Относительный прирост в данный момент |
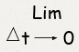 ∆x/∆t ∆x/∆t |
Производная |
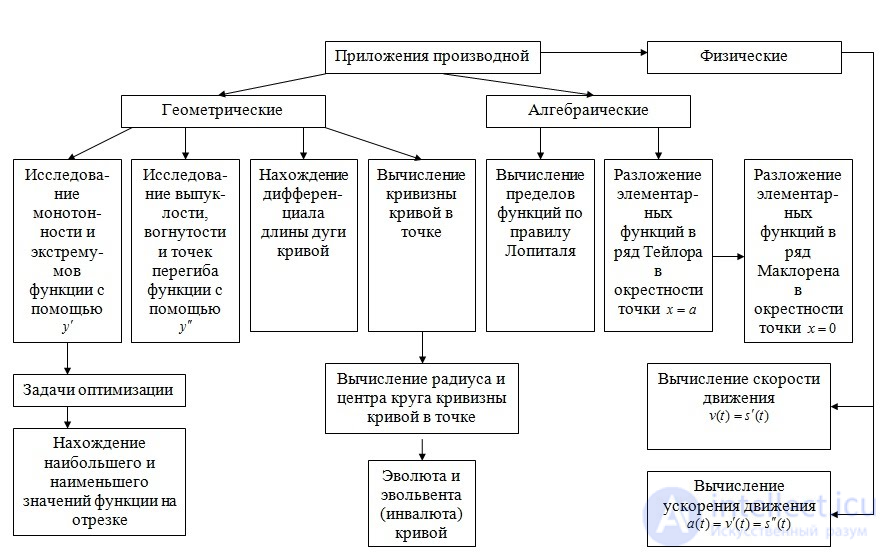
Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
наибольшее значение для сейсмогеодинамики имеют производные от скоростей движения земной коры, важнейшая из которых – градиент, характеризующий скорость деформации. Для поля вертикальной составляющей скорости в свое время были составлены карты модуля градиента [Гзовский, 1967; Николаев, Шенкарева, 1967].
2. Особенности электромагнитного поля земли
Высшие производныене только использовались при интерпретации потенциальных полей, но и способствовали развитию некоторых новых направлений в геологическом истолковании наблюденных аномалий: 1) локализация особых точек потенциальных функций; 2) разделение сложных аномалий, вызванных породами, залегающими на разной глубине; 3) ослабление регионального влияния; 4) изучение фигуры Земли; 5) решение задач редукции гравитационных наблюдений и т. д.
3. Радиоактивность ядерно- геоифзичексих показателей
4.Многие значения в экономической географии
5.Вывести формулу для вычисления численности населения на территории в момент времени t.
у’= к у
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует
Выведем формулу для вычисления численности населения наограниченной территории в момент времени t.
Пусть у = у(t)- численность населения.
Рассмотрим прирост населения за Δt = t-t0
Δy = k y Δt, где к = кр – кс –коэффициент прироста (кр –коэффициент рождаемости,кс – коэффициент смертности)
Δy:Δt=k y
При Δt→0 получим lim Δy/ Δt=у’.
В наших домах, на транспорте, на заводах : всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на ее продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.
Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.
Рассмотрим ситуацию: пусть y - издержки производства, а х -количество продукции, тогда x1- прирост продукции, а y1 -приращение издержек производства.
В этом случае производная выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство дополнительной единицы продукции.
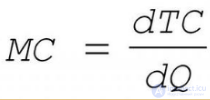
Где:
MC - предельные издержки (marginal costs);
TC - общие издержки (total costs);
Q - количество.
Производительность труда
Через производную можно определить и производительность труда:
Пусть функция u = u(t) выражает количество произведенной продукции u за время t. Необходимо найтипроизводительность труда в момент tο.
За период времени от tο до tο + Δt количество произведенной продукции изменится от значения uο = u(tο) до значения uο +Δu = u(tο + Δt). Тогда
средняя производительность труда за этот период времени Zср =Δu :Δt. Очевидно, что производительность труда в момент tο
можно определить как предельное значение средней производительности за период времени от tο до tο + Δt при Δt→ 0, т.е.
z = lim Zср = lim Δu/Δt = u'(t) при Δt→0
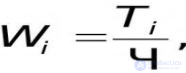
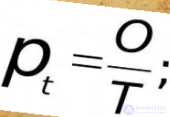
Задача по экономической теории.
Предприятие производит Х единиц некоторой однородной продукции в месяц. Установлено, что зависимость финансовых накопления предприятия от объема выпуска выражается формулой f(x)=-0,02x^3+600x -1000. Исследовать потенциал предприятия.
Функция исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений.
Таким образом , задачи ,решаемые с помощью производной, широко используются в производстве.
ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни
Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь свое применение в других темах и предметах.
А как ты думаешь, при улучшении производная, будет лучше нам? Надеюсь, что теперь ты понял что такое производная, таблица производных, приложения производных, применение производных, физическое приложение производной , геометрическое приложение производной и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление