5.5. План общего исследования функции, Исследование функции одной переменной методами дифференциального исчисления кратко

Привет, мой друг, тебе интересно узнать все про план общего исследования функции, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое план общего исследования функции, исследование функции , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

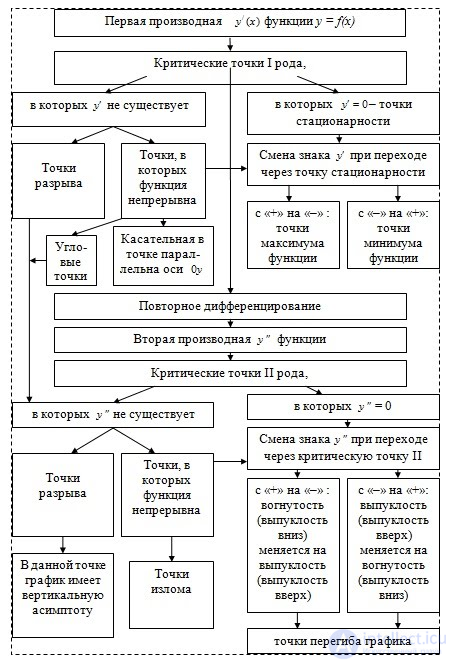
Полное исследование функции проводят по следующему плану:

1. Область определения функции.
2. Четность, нечетность, периодичность функции.
3. Непрерывность функции.
4. Асимптоты.
5. Нули функции и интервалы знакопостоянства.
6. Интервалы монотонности и экстремумы.
7. Выпуклость, вогнутость, точки перегиба.
8. Построение графика.

Исследование функции одной переменной методами дифференциального исчисления

Точка x0 называется точкой максимума (минимума) функции y=f (x), если существует такая δ–окрестность точки x0, что для всех 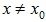из этой окрестности выполняется неравенство .

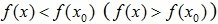Точки максимума и минимума функции называются точками экстремума (рис. 3.5).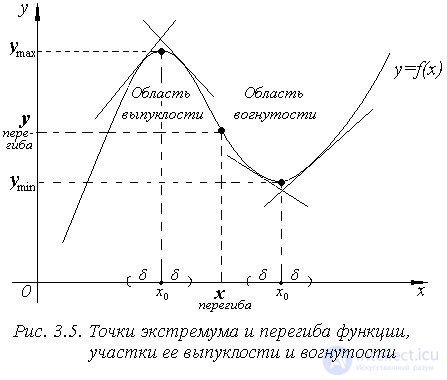

Теорема 3.15 (необходимое условие существования точек экстремума функции одной переменной). Если дифференцируемая функция y=f (x) имеет экстремум в точке x0, то ее производная в этой точке равна нулю или не существует

Точки, в которых производная функции либо равна нулю, либо не существует, называют критическими точками 1-го рода.

Критические точки, в которых производная функции равна нулю, называются точками стационарности.

Функция y=f (x) называется возрастающей на некотором интервале (a;b), если на этом интервале большему значению аргумента x соответствует большее значение переменной y, и убывающей, если большему значению аргумента x соответствует меньшее значение переменной y.

Для дальнейшего исследования критические точки помещают на числовую ось, которая делится этими точками на интервалы, после чего поверяют выполнение следующих достаточных условий.

Теорема 3.16 (достаточное условие возрастания и убывания функции одной переменной). Если на некотором интервале (a;b) функция y=f (x) дифференцируема и при этом ее производная 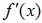положительна (отрицательна), то функция на данном интервале возрастает (убывает)

Теорема 3.17 (достаточное условие существования точек экстремума функции ). Если функция y=f (x) непрерывна и дифференцируема в некоторой δ –окрестности критической точки x0 и при переходе через нее производная 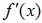меняет знак с плюса на минус, то точка x0 является точкой максимума; если с минуса на плюс, то точка x0 является точкой минимума функции

Те критические точки функции, для которых достаточное условие не выполняется, остаются просто критическими точками 1-го рода.

Критические точки 1-го рода, в которых производная не существует, делятся на классы:

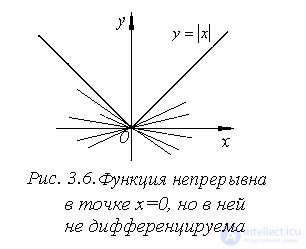
– точки, в которых функция непрерывна, но при выполнении теоремы 3.17 имеет в этих точках «острый» экстремум (угловые точки или точки излома) (рис. 3.6);

– точки, в которых функция непрерывна, но касательная в них к графику функции параллельна оси 0y (угловой коэффициент такой касательной

, то есть не существует); например, для функции 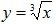такой точкой является x0=0;

– точки, в которых функция терпит разрыв (всегда переходят в класс критических точек 2-го рода).

Но проведенное таким образом исследование, не дает ответ на очень важный вопрос: как возрастает (убывает) функция – выпукло или вогнуто? Ответ на поставленный вопрос дает дальнейшее рассмотрение функции с помощью второй производной. Об этом говорит сайт https://intellect.icu . Дадим ряд необходимых определений.

Функция называется выпуклой (выпуклой вверх) на некотором интервале (a;b), если касательная, проведенная к графику функции в каждой точке этого интервала, лежит выше графика функции.

Функция называется вогнутой (выпуклой вниз) на некотором интервале (a;b), если касательная, проведенная к графику функции в каждой точке этого интервала, лежит ниже графика функции.

Точки, отделяющие участки выпуклости от участков вогнутости функции, называются ее точками перегиба (см. рис. 3.5).

Теорема 3.18 (необходимое условие существования точек перегиба функции). Если дважды дифференцируемая функция y=f (x) имеет перегиб в точке x0, то в этой точке вторая производная равна нулю или не существует

Точки, в которых вторая производная функции либо равна нулю, либо не существует, называют критическими точками 2-го рода.

Для дальнейшего исследования критические точки 2-го рода помещают на числовую ось, которая делится этими точками на интервалы, после чего поверяют выполнение следующих достаточных условий.

Теорема 3.19 (достаточное условие выпуклости и вогнутости функции). Если на некотором интервале (a;b) функция y=f(x) дважды дифференцируема и при этом ее вторая производная 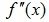положительна (отрицательна), то функция на данном интервале вогнута (выпукла)

Примечание. Очевидно, что на интервале выпуклости функция имеет точку максимума, а на интервале вогнутости – точку минимума (см. рис. 3.5).

Теорема 3.20 (достаточное условие существования точек перегиба функции). Если функция y=f(x) непрерывна и дважды дифференцируема в некоторой окрестности критической точки 2-го рода и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба функции

Те критические точки функции, для которых достаточное условие 3.19 не выполняется, остаются просто критическими точками 2-го рода. Критические точки 2-го рода, в которых вторая производная не существует, делятся на классы:

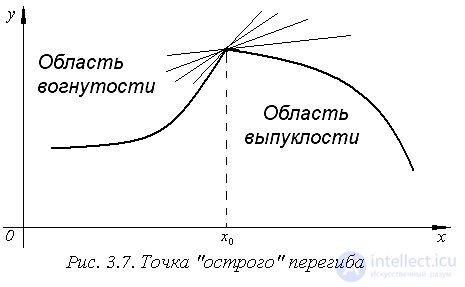
– точки, в которых функция непрерывна и при выполнении теоремы 3.20 имеет в этих точках «острый» перегиб, – в них можно провести к графику функции бесконечное множество касательных (рис. 3.7);

– угловые точки (переходят из критических точек первого рода);

– точки, в которых функция терпит разрыв (в точках разрыва 2-го рода график функции имеет вертикальную асимптоту).

Для окончательного перечисления точек экстремума и перегиба функции необходимо найти их ординаты, после чего выписать указанные точки двумя координатами.

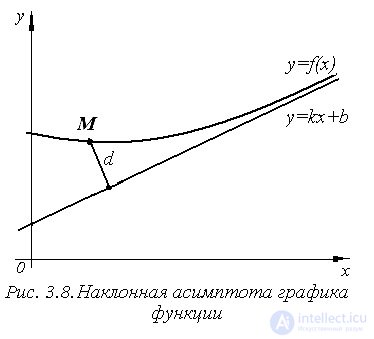
Для завершения исследования функции и построения графика необходимо проверить наличие у нее асимптот. Напомним, что асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат точки по кривой (рис. 3.8).

Асимптоты могут быть вертикальными, наклонными, горизонтальными.

Говорят, что прямая x=a является вертикальной асимптотой графика

.

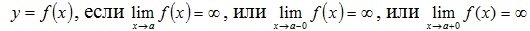Например, кривая 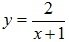имеет вертикальную асимптоту x=-1, так как .

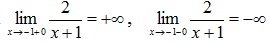Уравнение наклонной асимптоты ищем в виде y=kx+b (рис. 3.8).

Коэффициенты k и b находятся по формулам:

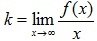(3.41)

и 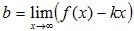. (3.42)

Верно и обратное: если существуют конечные пределы (3.41) и (3.42), то прямая y=kx+b является наклонной асимптотой.

Если хотя бы один из пределов (3.41) или (3.42) не существует или равен бесконечности, то кривая y=f (x) наклонной асимптоты не имеет.

В частности, если k=0, то . Поэтому y=b – уравнение горизонтальной асимптоты.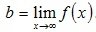

Примечание. Асимптоты графика функции y=f (x) при ∆x→+∞ и ∆x→–∞ могут быть разными. Поэтому при нахождении пределов (3.41) и (3.42) следует отдельно рассматривать случай, когда ∆x→+∞ и когда ∆x→–∞.

Пример 3.16. Исследовать методами дифференциального исчисления и построить график функции .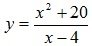

Решение.

1. Область определения: .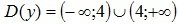

2. Исследуем функцию на непрерывность и классифицируем ее точки разрыва. Заданная функция непрерывна всюду, кроме точки x=4. Вычислим односторонние пределы в этой точке:

.

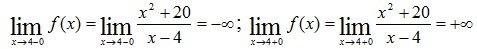Таким образом, точка x=4 является для заданной функции точкой разрыва второго рода, а прямая x=4 – вертикальной асимптотой графика.

3. Проведем исследование функции методами дифференциального вычисления. Для исследования на экстремум и промежутки монотонности вычислим первую производную: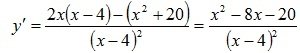. На основании теоремы 3.15 найдем критические точки первого рода, в которых производная равна нулю или не существует

.

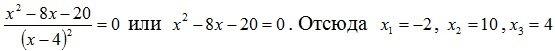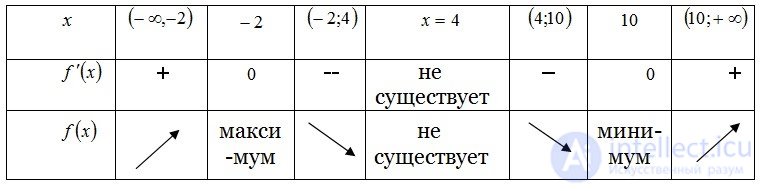
Результаты исследования заданной функции с помощью первой производной занесем в таблицу 3.1, основываясь на теоремах 3.16, 3.17.

Таблица 3.1

Исследование функции с помощью первой производной

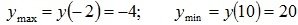. Следовательно, A (–2; –4) – точка максимума, а B(10; 20) – точка минимума функции.

4. Исследуем функцию на выпуклость, вогнутость и точки перегиба с помощью второй производной, основываясь на теоремах 3.23, 3.24:

.

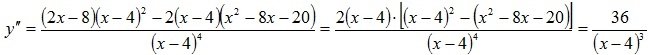Так как 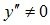, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости. Результаты исследования занесем в следующую таблицу 3.2.

Таблица 3.2

Исследование функции с помощью второй производной

5. Исследуем график функции на наличие наклонных и горизонтальных асимптот, уравнение которых как прямых линий y=kx+b.

Согласно (3.41) 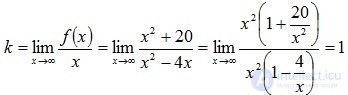. Так как 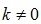, то горизонтальных асимптот не существует.

Согласно (3.42) .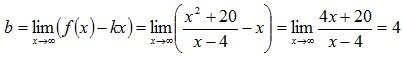

Таким образом, прямая y=x+4 – наклонная асимптота графика.

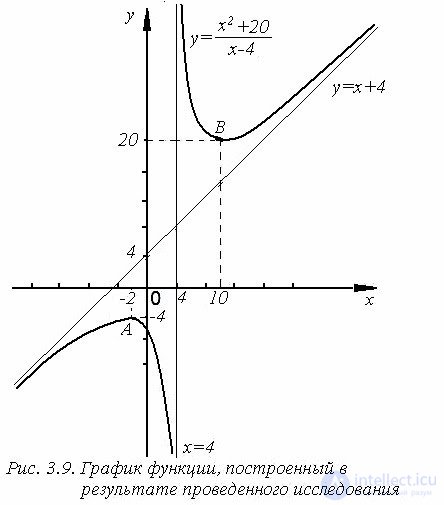
Очевидно, график заданной функции пересекает ось 0y в точке (0; –5) и, на основе обобщения результатов всех предыдущих исследований, имеет вид, представленный на рисунке 3.9

Тебе нравиться план общего исследования функции? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое план общего исследования функции, исследование функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление