2.6.6. Экстремумы ФМП

Привет, мой друг, тебе интересно узнать все про экстремумы фмп, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое экстремумы фмп , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

Точка  M_o(x_o, y_o)  называется точкой максимума функции  , если для всех точек  (x, y), принадлежащих достаточно малой окрестности точки  M_o(x_o, y_o), выполняется неравенство 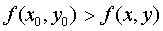 . Значение функции    в точке максимума называется максимумом функции.

Точка  M_o(x_o, y_o)  называется точкой минимума функции  , если для всех точек  (x, y), принадлежащих достаточно малой окрестности точки  M_o(x_o, y_o), выполняется неравенство  . Об этом говорит сайт https://intellect.icu . Значение функции    в точке максимума называется минимумом функции.

Точки максимума и минимума функции называются точками экстремума функции, а значения функции в этих точках называются экстремумами функции.

Необходимое условие существования экстремума ФМП: если дифференцируемая функция    достигает экстремума в точке  M_o(x_o, y_o), то ее частные производные первого порядка в этой точке равны нулю, т.е.  .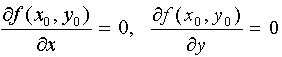

Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.

Достаточное условие существования экстремума ФМП:
пусть  M_o(x_o, y_o)  - стационарная точка функции  .
Обозначим: 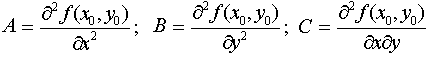   и составим соотношение  .

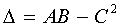Тогда:

• если  Δ > 0, то значение функции    есть экстремум, причем это максимум, если  A < 0  и минимум, если  A > 0;
• если  Δ < 0, то значение функции    экстремумом не является;
• если  Δ = 0, то требуется дальнейшее исследование.

Тебе нравиться экстремумы фмп? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое экстремумы фмп и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление