2.1. Понятие предела и непрерывности функции в точке, классификация точек разрыва функции одной переменной кратко

Привет, мой друг, тебе интересно узнать все про понятие предела функции, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое понятие предела функции, предел функции, непрерывность функции , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении ее аргумента к данной точке. Одно из основных понятий математического анализа.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, являющихся образами точек такой последовательности элементов области определения функции, которая сходится к точке, в которой рассматривается предел. Если такой предел существует, то говорят, что функция сходится к указанному значению, иначе говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения. Это позволяет говорить о стремлении аргумента функции к данной точке. Предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т. н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

График функции, предел которой при аргументе, стремящемся к бесконечности, равен

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удаленной точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция в заданной точке сама стремится к бесконечности. Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции в данной точке означает, что для любого заранее заданного значения области значений существует окрестность этого значения такая, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной в данной точке.

Определение непрерывности функции

Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определенным на подмножестве вещественных чисел и принимающим вещественные значения.

Определение предела функции

Пусть функция 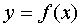определена в окрестности числа 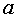(при функция ƒ может быть не определена). Об этом говорит сайт https://intellect.icu . Число А называется пределом функции при x , стремящемся к 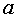( ), если для любого сколь угодно малого числа ε > 0 найдется такое число δ > 0 , что для всех x, удовлетворяющих условию 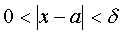выполняется неравенство .

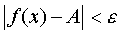Выражение 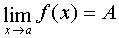означает, что предел функции 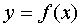при x, стремящемся к 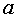, равен А.

Если для любого сколь угодно большого положительного числа М найдется такое число δ > 0 , что для всех x, удовлетворяющих условию 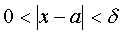, выполняется неравенство 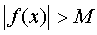, то говорят, что функция является бесконечно большой величиной при x, стремящемся к 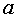, и записывают: .

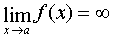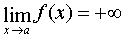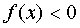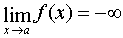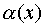Если при этом значения , то пишут: , а если , то пишут: . Если , то функция называетсябесконечно малой величиной при x, стремящемся к .

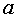Рассмотрим функцию , определенную на некотором множестве {\displaystyle X}, которое имеет предельную точку (которая, в свою очередь, не обязана ему принадлежать). Существуют разные определения предела функции, сформулированные Гейне, Коши.

Предел функции по Гейне

Значение называется пределом (предельным значением) функции в точке , если для любой последовательности точек , сходящейся к , но не содержащей в качестве одного из своих элементов (то есть в проколотой окрестности ), последовательность значений функции сходится к .

Предел функции по Коши

Значение называется пределом (предельным значением) функции в точке , если для любого наперед взятого положительного числа найдется отвечающее ему положительное число такое, что для всех аргументов {\displaystyle x}, удовлетворяющих условию , выполняется неравенство: .

Понятие предела и непрерывности функции в точке,

классификация точек разрыва функции одной переменной

Тебе нравиться понятие предела функции? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое понятие предела функции, предел функции, непрерывность функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление