Лекция
Сразу хочу сказать, что здесь никакой воды про неопределенность, и только нужная информация. Для того чтобы лучше понимать что такое неопределенность, отношение эквивалентности , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Неопределенности в математиеском анализе — это выражения, значение которых не определено котрорые при вычислении пределов зачастую появляются
отношение эквивалентности — бинарное отношение между элементами данного множества, свойства которого сходны со свойствами отношения равенства.
Бесконечно малые величины имеют фундаментальное значение в математическом анализе. Например, понятие предела функции можно сформулировать, положив в основу концепцию бесконечно малой функции. Бесконечно большая функция представляет собой величину, обратную бесконечно малой. Фактически любой раздел дифференциального и интегрального исчисления опирается на анализ бесконечно малых.
Концепция эквивалентных бесконечно малых функций позволяет существенно упростить процедуру раскрытия неопределенностей различного вида и свести вычисление пределов сложных выражений к тривиальным преобразованиям комбинаций степенных функций.
Перечислим основные формы неопределенностей:
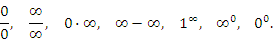
Под
неопределенность ю вида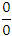 
понимается отношение двух бесконечно малых величин. Неопределенность вида 
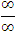возникает при делении одной бесконечно большой величины на другую. Аналогично интерпретируются и другие формы неопределенностей.
Любая форма неопределенности может быть преобразована к неопределенности вида 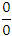. Действительно, пусть 
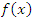и 
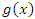– бесконечно большие функции в окрестности некоторой точки. Тогда
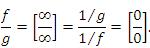
Аналогично,
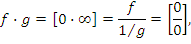
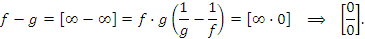
Для преобразования форм неопределенностей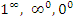 
к виду 
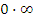(и, следовательно, к виду 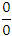) можно использовать логарифмическое тождество
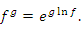
Пусть, например,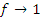 
и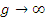 
при x → a. Тогда
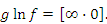
Аналогично,
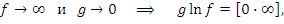
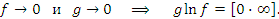
Отношение эквивалентности (
) на множестве 
— это бинарное отношение, для которого при любых 
из выполнены следующие условия:
;
, то 
; и 
, то 
.Запись вида «» читается как «
эквивалентно 
».
Классом эквивалентности 
элемента 
называется подмножество элементов, эквивалентных ; то есть,
.
Из вышеприведенного определения немедленно следует, что если 
, то 
.
Фактормножество — множество всех классов эквивалентности заданного множества по заданному отношению , обозначается 
.
Для класса эквивалентности элемента используются следующие обозначения: 
, 
, 
.
Множество классов эквивалентности по отношению является разбиением множества.
»), тривиальное отношение эквивалентности на любом множестве, в частности, вещественных чисел.
»).»).
») (но только если дополнительно к принятому определению считать каждую прямую параллельной самой себе).Говорят, что функция 
эквивалентна функции 
при 
, если она допускает представление вида 
, где 
при . Об этом говорит сайт https://intellect.icu . В этом случае пишут 
, напоминая при необходимости, что речь идет о сравнении функций при . Если 
при 
, эквивалентность функций и при , очевидно, равносильна соотношению 
.
Множество всех классов эквивалентности, отвечающее отношению эквивалентности , обозначается символом и называется фактормножеством относительно . При этом сюръективное отображение
называется естественным отображением (или канонической проекцией) на фактормножество .
Пусть и 
— множества, 
— отображение, тогда бинарное отношение 
, определенное правилом
,
является отношением эквивалентности на . При этом отображение 
индуцирует отображение 
, определяемое правилом
или, что то же самое,
.
При этом получается факторизация отображения на сюръективное отображение 
и инъективное отображение 
.
А как ты думаешь, при улучшении неопределенность, будет лучше нам? Надеюсь, что теперь ты понял что такое неопределенность, отношение эквивалентности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но содержательно про неопределенность
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление