3. Непрерывность функции 2.3.1. Непрерывные и разрывные функции

Привет, мой друг, тебе интересно узнать все про непрерывность функции непрерывные, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое непрерывность функции непрерывные, разрывные функции , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

Пусть функция 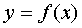   определена в окрестности числа  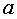. Функция  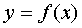  называется непрерывной в точке  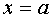, если:

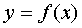•    функция    определена в некоторой окрестности точки  ;
•    . 

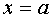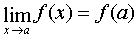Функция 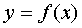   называется непрерывной на интервале  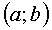, если она непрерывна в каждой точке этого интервала. Об этом говорит сайт https://intellect.icu . Если говорят, что функция  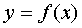 непрерывна на отрезке  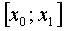, то при этом подразумевают, что функция  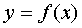  непрерывна на некотором интервале  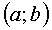, содержащем отрезок  .

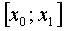Элементарные функции непрерывны в своей области определения, точнее, на наибольшем открытом множестве, содержащемся в области определения. Например, функция 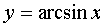   определена на отрезке [-1; 1], а непрерывна на интервале (1; 1).

Тебе нравиться непрерывность функции непрерывные? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое непрерывность функции непрерывные, разрывные функции и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление