Лекция
Привет, Вы узнаете о том , что такое ноль в нулевой степени, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ноль в нулевой степени , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Выражение 0⁰ (ноль в нулевой степени) многие учебники считают неопределенным и лишенным смысла . Связано это с тем, что функция двух переменных f(x,y)=xy в точке (0,0)
имеет неустранимый разрыв. В самом деле, вдоль положительного направления оси X,
где y=0,
она равна единице, а вдоль положительного направления оси Y,
где x=0,
она равна нулю. Поэтому никакое соглашение о значении 0⁰ не может дать непрерывную в нуле функцию.
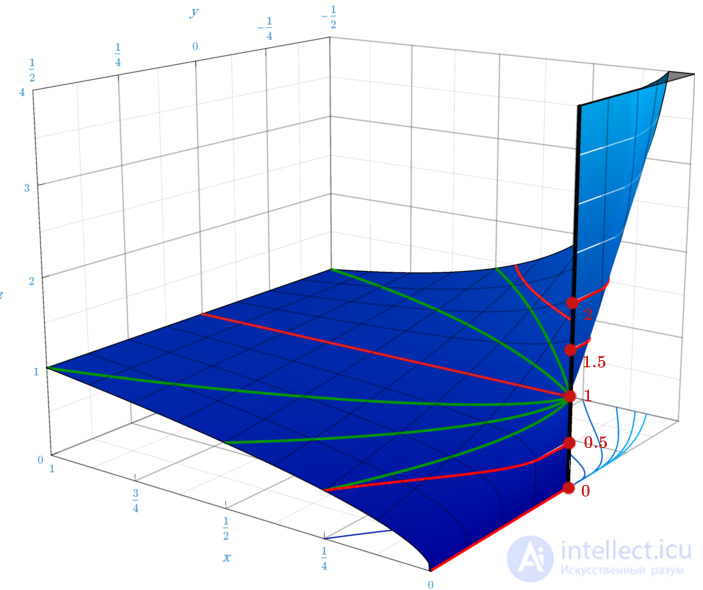
График функции z = xy вблизи x = 0, y = 0
Некоторые авторы предлагают принять соглашение о том, что 00 равно 1. В пользу подобного варианта приводятся несколько доводов. Например, разложение в ряд экспоненты:
можно записать короче, если принять :
(рассматриваемое соглашение используется при x=0, n=0 ).
Другое обоснование соглашения опирается на «Теорию множеств» Бурбаки : число различных отображений n-элементного множества в m-элементное равно mn,
при m=n=0 получаем отображение пустого множества в пустое, а оно единственно. Разумеется, это нельзя считать доказательством (соглашения не нуждаются в доказательствах), тем более что в самой теории множеств соглашение
не используется.
В любом случае соглашение чисто символическое, и оно не может использоваться ни в алгебраических, ни в аналитических преобразованиях из-за разрывности функции в этой точке, в противном случае может возникнуть ошибка. Пример для аналитических вычислений: функция
где a
— произвольное положительное вещественное число. При t→0 мы получаем неопределенность типа
и, если не отличать тип предела
(где каждый из нулей обозначает стремление к нулю) и значение
(где каждый из нулей и есть ноль), можно ошибочно посчитать, что предел равен 1. На самом деле данное выражение тождественно равно a−1.
Это означает, что бесконечно малая в бесконечно малой степени может в пределе дать любое значение, не обязательно единицу. Аналогичные ошибки могут быть сделаны, если использовать соглашение в алгебраических преобразованиях.
Дискуссия по поводу определения продолжается, по крайней мере, с начала XIX века. Многие математики тогда принимали соглашение 00=1
, но в 1821 году Коши причислил 00
к неопределенностям, таким, как 00.
В 1830-х годах Либри опубликовал неубедительный аргумент в пользу
(см. Об этом говорит сайт https://intellect.icu . Функция Хевисайда § История), и Мебиус встал на его сторону, ошибочно заявив, что
всякий раз, когда
. Обозреватель, который подписал свое имя просто как «S», предоставил приведенный выше контрпример
, и это немного успокоило дебаты. Больше исторических деталей можно найти в статье Кнута (1992) .
Более поздние авторы интерпретируют ситуацию выше по-разному. Часть математиков считает, что 00 должно быть определено как 1. Например, Кнут (1992) уверенно утверждает, что
«должно быть 1», делая различие между значением
, которое должно равняться 1, как это было предложено Либри, и предельной формой 00
(аббревиатура для предела
где f(x),g(x)→0 ), что обязательно является неопределенностью, как указано Коши: «И Коши, и Либри были правы, но Либри и его защитники не понимали, почему истина на их стороне» . Авторитетный сайт MathWorld, приведя мнение Кнута, все же констатирует, что обычно значение 00
считается неопределенным, несмотря на то, что соглашение 00=1
позволяет в некоторых случаях упростить запись формул .
Другие математики утверждают, что наилучшее значение для зависит от контекста, и поэтому определение его раз и навсегда проблематично[10]. Согласно Бенсону (1999), «Выбор, следует ли определять 00,
основан на удобстве, а не на правильности. Если мы воздержимся от определения 00
, то некоторые утверждения становятся излишне неудобными. <…> Консенсус заключается в использовании определения 00=1
, хотя есть учебники, которые воздерживаются от определения
»[11].
В России Большая российская энциклопедия, Большая советская энциклопедия, Математический энциклопедический словарь, Справочник по элементарной математике Выгодского, школьные учебники и другие источники однозначно характеризуют 00 как выражение, не имеющее смысла (неопределенность).
Если даны две функции f(x) и g(x), которые стремятся к нулю, то предел в общем случае, как показано выше, может быть любым. Таким образом, с этой точки зрения
является неопределенностью. Для нахождения предела
в этом случае пользуются методами раскрытия неопределенности — как правило, сначала взяв логарифм от данного выражения:
,
а потом воспользовавшись правилом Лопиталя.
Однако при определенных условиях этот предел будет действительно равен единице. А именно: если функции f и g
являются аналитическими в точке 0
(то есть в некоторой окрестности точки 0
совпадают со своим рядом Тейлора), и f(0)=g(0)=0
, а f(x)>0
в окрестности (0,δ)
, то предел f(x)g(x)
при x
стремящемся к нулю справа равен 1[12][13][14].
Например, таким образом можно сразу убедиться, что
При этом надо не забывать, что если хотя бы одна из функций не разлагается в ряд Тейлора в точке 0 или f(x) тождественно равен 0, то предел может быть любым, или может не существовать. Например,
Для комплексных чисел u,v выражение вида uv для u≠0 многозначно и определяется как
, Однако комплексный логарифм
не определен ни в какой своей ветви, и это лишает смысла любое соглашение не только для ,
но и для любого ,
хотя часть авторов предлагает при z≠0 принять соглашение
Стандарт IEEE 754-2008, описывающий формат представления чисел с плавающей запятой, определяет три функции возведения в степень[18]:
NaN или бесконечности.NaN.x=NaN.Во многих языках программирования
ноль в нулевой степени равен 1. Например, в C++: pow(0, 0) == 1, в языке Haskell это верно для всех трех стандартных операций возведения в степень: 0^0 == 1, 0^^0 == 1, 0**0 == 1. То же касается и стандартного калькулятора MS Windows.
Хотя общеизвестно, что — это неопределенность, поведение некоторых функций, возвращающих в данном случае 1
, не является результатом соглашения или ошибкой, оно имеет логическое обоснование. Дело в том, что в компьютерной арифметике числовые данные подразделяются на целые и вещественные. Это может неявно использоваться в некоторых функциях, реализующих операцию возведения в степень. Например, так сделано в калькуляторе Windows и функции
pow в C++. Для целого и вещественного показателя степени используются различные алгоритмы, и функция возведения в степень анализирует показатель: если он равен целому числу, то вычисление степени идет по другому алгоритму, в котором отрицательные и нулевое основания степени являются допустимыми. Если показатель степени принадлежит множеству целых чисел и равен 0, а основание - вещественное число, то операцию следует определять не иначе как
. Поскольку 0 в показателе точный, предельный переход касается только основания и (в отличие от случая, когда показатель тоже вещественный) определен однозначно и равен 1 . Сказанное в полной мере относится и к случаю вычисления выражения
.
Исследование, описанное в статье про ноль в нулевой степени, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое ноль в нулевой степени и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но содержательно про ноль в нулевой степени
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление