Лекция
степень числа — это математическая операция, при которой число умножается само на себя определенное количество раз.
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
Степень числа записывается в виде an, где:
Положительный показатель степени: an=a×a×a×⋯×a (где число aaa умножается на себя nnn раз).
Например, 
Отрицательный показатель степени: 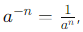 , где a≠0 . Отрицательная степень означает, что мы берем обратное значение числа, возведенного в положительную степень.
, где a≠0 . Отрицательная степень означает, что мы берем обратное значение числа, возведенного в положительную степень.
Например,  .
.
Нулевая степень: Для любого числа aaa, кроме нуля, выполняется правило: a0=1.
Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулем.
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберемся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращенное обозначение.
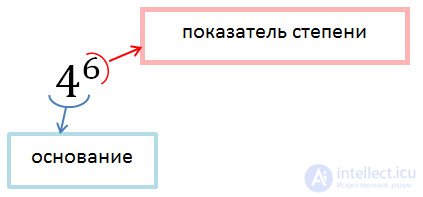
Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 46 и произносят «четыре в шестой степени».
4 • 4 • 4 • 4 • 4 • 4 = 46
Выражение 46 называют степенью числа, где:
В общем виде степень с основанием "a" и показателем "n" записывается с помощью выражения:
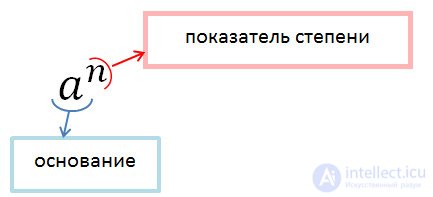
Степенью числа "a" с натуральным показателем "n", бóльшим 1, называется произведение "n" одинаковых множителей, каждый из которых равен числу "a".

Запись an читается так: «а в степени n» или «n-ая степень числа a».
Исключение составляют записи:
Конечно, выражения выше можно читать и по определению степени:
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1
Выражение 00 (ноль в нулевой степени) считают лишенным смыслом.
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
Пример. Возвести в степень.
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 • 3 • 3 • 3 |
| 4 • 4 • 4 • 4 |
| 81 |
| 256 |
Основание степени (число, которое возводят в степень) может быть любым числом - положительным, отрицательным или нулем.
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того четным или нечетным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
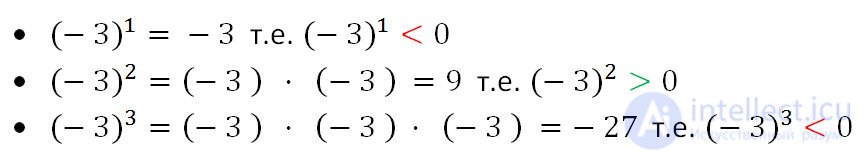
Из рассмотренных примеров видно, что если отрицательное число возводится в нечетную степень, то получается отрицательное число. Так как произведение нечетного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в четную степень, то получается положительное число. Так как произведение четного количество отрицательных сомножителей положительно.
Отрицательное число, возведенное в четную степень, есть число положительное.
Отрицательное число, возведенное в нечетнуюстепень, - число отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)4 и -54 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (- 5)4 означает найти значение четвертой степени отрицательного числа.
(- 5)4 = (- 5) • (- 5) • (- 5) • (- 5) = 625
В то время как найти -54 означает, что пример нужно решать в 2 действия:
Пример. Вычислить: - 62 - (- 1)4
- 62 - (- 1)4 = - 37
Когда вы решаете выражения, включающие степени, следует соблюдать определенный порядок действий:
В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:

Возведение в степень и работа со степенями применяются в различных областях науки и техники. Вот несколько примеров применения:
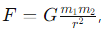 2 где расстояние между телами rrr возводится в квадрат.
2 где расстояние между телами rrr возводится в квадрат.
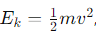 , где скорость vvv возводится в квадрат.
, где скорость vvv возводится в квадрат. , где напряжение V возводится в квадрат.
, где напряжение V возводится в квадрат. , включает возведение в степень, где t — количество лет, а n — частота начисления процентов.
, включает возведение в степень, где t — количество лет, а n — частота начисления процентов.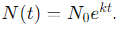 .
.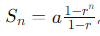 , где n — степень множителя r.
, где n — степень множителя r. продукты, скорость может выражаться как
продукты, скорость может выражаться как 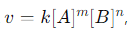 , где m и n — степени концентраций A и B.
, где m и n — степени концентраций A и B.Возведение в степень также играет важную роль в сокращении вычислений и оптимизации математических операций. Вот несколько примеров, как степени упрощают или сокращают вычисления:
Вместо того чтобы выполнять длительные вычисления с многократным умножением одного и того же числа, можно воспользоваться возведением в степень. Например:
Возведение в степень позволяет быстро вычислять большие значения, используя свойства степеней, такие как:
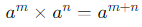 (суммирование показателей степени),
(суммирование показателей степени), (вычитание показателей степени),
(вычитание показателей степени),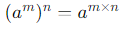 (произведение показателей степени).
(произведение показателей степени).Эти свойства уменьшают количество операций и ускоряют процесс решения.
При разработке алгоритмов в программировании часто используется возведение в степень для ускорения вычислений, например:
Пример быстрого возведения в степень:
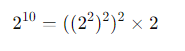
Степени помогают эффективно выражать и работать с очень большими числами. Например, вместо того чтобы писать большие числа вручную, можно использовать экспоненциальные формы, такие как:
Это удобно в астрономии, физике и других науках, где часто используются очень большие числа.
Степени играют важную роль в упрощении решения уравнений, особенно полиномиальных и экспоненциальных. Применение свойств степеней позволяет свести сложные выражения к более простым формам.
Пример:
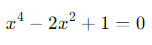
Можно заменить x2 на новую переменную y, и уравнение становится квадратичным:
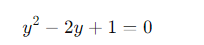
Это существенно упрощает вычисления.
Возведение в степень помогает записывать сложные выражения в компактной форме, что не только облегчает понимание, но и ускоряет вычисления. Например, многочлены и полиномиальные выражения записываются с помощью степеней, что экономит место и делает математические расчеты более структурированными.
В задачах, где происходит экспоненциальный рост (например, рост численности населения, увеличение капитала при сложных процентах или распространение информации), возведение в степень позволяет прогнозировать результат через большие промежутки времени, сокращая необходимость в пошаговых вычислениях.
Таким образом, возведение в степень существенно сокращает вычисления, как в математических задачах, так и в практических приложениях, благодаря удобным правилам и свойствам степеней, а также возможности выражать большие числа и сложные выражения в сжатой форме.
Таким образом, возведение в степень — это ключевой инструмент для решения множества практических задач в науке и технике.
Комментарии
Оставить комментарий
Арифметика
Термины: Арифметика