Лекция
Привет, мой друг, тебе интересно узнать все про свойства арифметических корней, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое свойства арифметических корней, вынесение множителя под корень, вынесение множителя под корень , настоятельно рекомендую прочитать все из категории Арифметика.
. Об этом говорит сайт https://intellect.icu
Все свойства обычных (целых) степеней распространяются также и на дробные степени.
При умножении одинаковых оснований, степени чисел складываются:
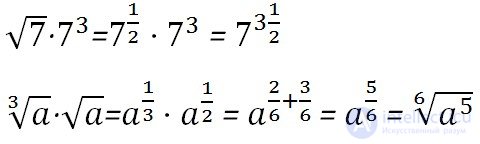
При делении одинаковых оснований, степени чисел вычитаются:
При возведение в степень числа, которое уже и так находится в степени, старая степень перемножается с новой:
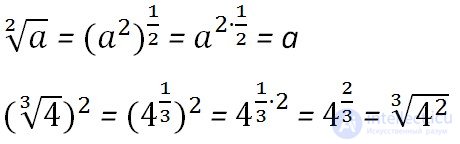
Свойств корней много, но мы выделяем всего два, так как считаем их наиболее важными.
Корень из произведения - это произведение корней.
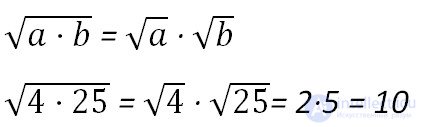
Корень из дроби - это корень из числителя и корень из знаменателя.
Свойства корней - при умножении, делении, множественного извлечения, вынесения и внесения множителя под корень
Если я не полностью рассказал про свойства арифметических корней? Напиши в комментариях Надеюсь, что теперь ты понял что такое свойства арифметических корней, вынесение множителя под корень, вынесение множителя под корень и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но содержательно про свойства арифметических корней
Комментарии