Лекция
Привет, мой друг, тебе интересно узнать все про функция действительного аргумента, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое функция действительного аргумента , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Целые положительные числа 1,2,3,┘ называются натуральными.
Добавив к натуральным числам все дробные числа и нуль, а также рассматривая не только положительные числа, но и отрицательные, получим рациональные числа. Каждое рациональное число может быть записано в виде конечной десятичной или бесконечной периодической десятичной дроби.
Иррациональными числами называются бесконечные непериодические дроби.
Действительными (или вещественными) числами называется совокупность рациональных и иррациональных чисел.
δ - окрестностью точки xo называется множество точек, задаваемое неравенством 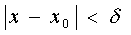 или интервалом
или интервалом 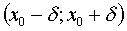 .
.
Возьмем некоторое множество значений переменной величины x и обозначим его через D. Если каждому значению x из множества D по какому-нибудь правилу поставлено в соответствие одно или несколько определенных значений другой величины y, то говорят, что величина есть функция величины x. При этом величина x называется аргументом функции y, а множество D - областью определения функции y.
Функция задается выражением 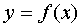 , которое означает, что для нахождения значения y над x необходимо выполнить некоторые действия.
, которое означает, что для нахождения значения y над x необходимо выполнить некоторые действия.
Функция, определенная на множестве натуральных чисел, называется числовой последовательностью.
Элементарной функцией называется функция, которую можно задать одной формулой, составленной из основных элементарных функций и постоянных при помощи конечного числа арифметических действий и конечного числа операций взятия функции от функции.
Основными элементарными функциями являются следующие функции.
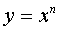 , где n - действительное число.
, где n - действительное число. , где
, где 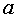 - положительное число и
- положительное число и 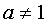 .
. , где основание логарифма
, где основание логарифма 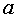 - положительное число и
- положительное число и 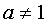 .
.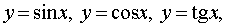
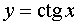
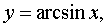
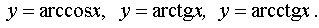
Функция 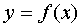 называется четной, если при изменении знака у любого значения аргумента значение функции не изменяется:
называется четной, если при изменении знака у любого значения аргумента значение функции не изменяется: 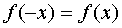 .
.
Функция 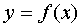 называется нечетной, если при изменении знака у любого значения аргумента изменяется только знак значения функции, а абсолютная величина этого значения остается без изменения:
называется нечетной, если при изменении знака у любого значения аргумента изменяется только знак значения функции, а абсолютная величина этого значения остается без изменения: 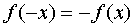 .
.
Функция 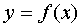 называется периодической, если существует такое постоянное число
называется периодической, если существует такое постоянное число 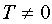 , что от прибавления его к любому значению аргумента значение функции не изменяется:
, что от прибавления его к любому значению аргумента значение функции не изменяется: 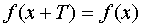 .
.
Тебе нравиться функция действительного аргумента? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое функция действительного аргумента и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но содержательно про функция действительного аргумента
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление