Лекция
Привет, Вы узнаете о том , что такое деление на ноль, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое деление на ноль , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
деление на ноль в математике — деление, при котором делитель равен нулю. Такое деление может быть формально записано как , где a — делимое.
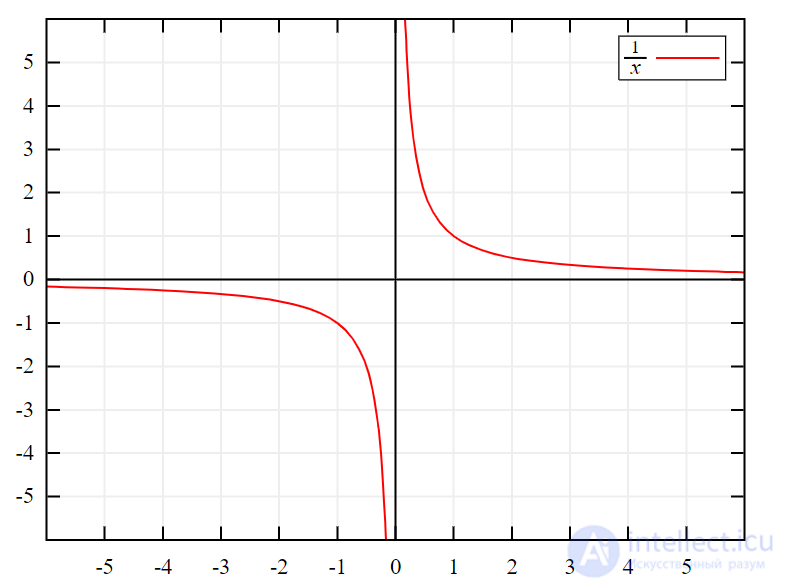
Функция y = 1⁄x . Когда x идет к нулю справа, y стремится к бесконечности. Когда x идет к нулю слева, y направляется к минус бесконечности.
В арифметике с вещественными числами данное выражение не имеет смысла, так как:
Исторически одна из первых ссылок на математическую невозможность присвоения значения а⁄0 содержится в критике Джорджа Беркли исчисления бесконечно малых.
Деление на ноль недопустимо во многих алгебраических структурах (например, в полях, кольцах). Об этом говорит сайт https://intellect.icu . Однако понятие кольца можно расширить так, чтобы деление на ноль было возможным. Получившаяся структура называется колесо.
В то же время, согласно определению делимости целых чисел, если для некоторого целого числа a и целого числа b
существует такое целое число q
, что a=qb
, то говорят, что число a
делится нацело на b (обозначается
) или что b делит a (обозначается b∣a).
В соответствии с этим определением выполняются следующие свойства:
0⋮a,
и частное (при a≠0) равно нулю.
a⋮0 ⇒ a=0,
причем частное в этом случае не определено.
Поскольку при умножении любого числа на ноль в результате мы всегда получаем ноль, при делении обеих частей выражения x × 0 = y × 0, верного вне зависимости от значения x и y, на 0 получаем неверное в случае произвольно заданных переменных выражение x = y. Поскольку ноль может быть задан не явно, но в виде достаточно сложного математического выражения, к примеру в форме разности двух значений, сводимых друг к другу путем алгебраических преобразований, такое деление может быть достаточно неочевидной ошибкой. Незаметное внесение такого деления в процесс доказательства с целью показать идентичность заведомо разных величин, тем самым доказывая любое абсурдное утверждение, является одной из разновидностей математического софизма .
В программировании, в зависимости от языка программирования, типа данных и значения делимого, попытка деления на ноль может приводить к различным последствиям. Принципиально различны последствия деления на ноль в целой и вещественной арифметике:
Случайное деление на ноль в компьютерной программе порой становится причиной дорогих или опасных сбоев в работе управляемого программой оборудования. К примеру, 21 сентября 1997 года в результате деления на ноль в компьютеризированной управляющей системе крейсера USS Yorktown (CG-48) Военно-морского флота США произошло отключение всего электронного оборудования в системе, в результате чего силовая установка корабля прекратила свою работу.
Исследование, описанное в статье про деление на ноль, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое деление на ноль и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но содержательно про деление на ноль
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление