Примеры решения задач к разделу пределы и производная. дифференциальое исчисление

Привет, мой друг, тебе интересно узнать все про ы решения задач к разделу пределы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ы решения задач к разделу пределы, производная дифференциальое исчисление , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

Пример N 1

Вычислить: . 

Решение.

Числитель и знаменатель дроби неограниченно возрастают при  .  В этом случае говорят, что имеет место неопределенность типа 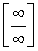   . Разделим числитель и знаменатель дроби на старшую степень переменной  x  , в нашем случае - на  x²  :

 . 

 

Так как при    каждая из дробей    .

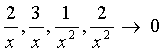Ответ:  3

Пример N 2

Вычислить:   .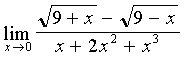

Решение.

Числитель и знаменатель дроби при    также стремятся к нулю. В этом случае имеет место неопределенность типа 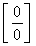 .  Умножим числитель и знаменатель дроби на    :

  

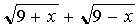Знаменатель дроби    при    , следовательно    .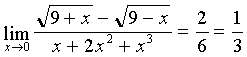

Ответ:    .

Пример N 3

Вычислить:  .

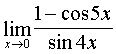Решение.

Воспользуемся тригонометрической формулой 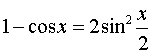   и заменим числитель и знаменатель дроби эквивалентными бесконечно малым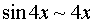и    и    :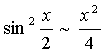

  

Ответ:  0.

Пример N 4

Вычислить:   .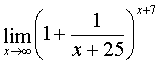

Решение.

При    выражение 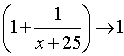   , а  (x +7)  неограниченно возрастает. 
В этом случае имеет место неопределенность типа 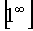   . Об этом говорит сайт https://intellect.icu . Рекомендуется использовать второй замечательный предел  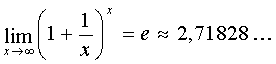  или следствие из него: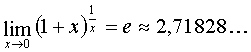  

Так как 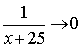   при    , то 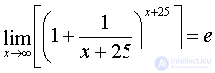   . Учитывая, что  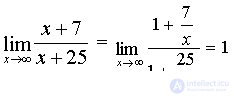  (см. пример N1), окончательно получаем   

Ответ:   .

Пример N 5

Вычислить:   .

Решение.

Так как при    выражение    , имеет место неопределенность типа 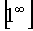   . Преобразуем функцию так, чтобы использовать второй замечательный предел. Выделим целую часть из дроби (для этого к числителю дроби прибавим и отнимем 3):   , тогда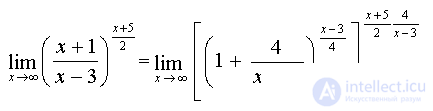 
  

Так как 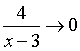   при    , то    .

Учитывая, что 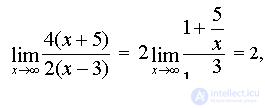   окончательно получим: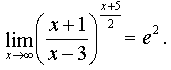  

Ответ:   .

Пример N 6

Исследовать функцию 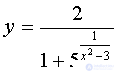   на непрерывность и построить схематически ее график.

Решение.

Данная функция терпит разрыв в точках    и 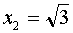  , так как при этих значениях знаменатель дроби    обращается в нуль. Исследуем характер разрыва в каждой из этих точек.

Для этого найдем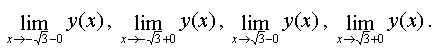   

Для точки    :

  

Так как
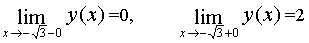   и    , то в точке    функция имеет разрыв первого рода или скачок.

Для точки    :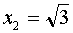

  

Таким образом, для точк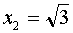и        и 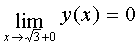     , значит, и при  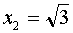  функция также терпит разрыв первого рода или скачок. Для схематического построения графика исследуем поведение функции при   

  

Следовательно, при    график функции находится около прямой  y = 1  . Найдем точку пересечения графика с осью ОУ:

  .

Ответ:  Схематический график функции (рис. 8):

Рис. 8

Пример N 7

Найти производную функции    .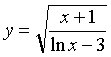

Решение.

Преобразуем квадратный корень в степень: .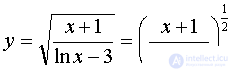 

Данная функция - сложная, используем последовательно формулы: производная степенной функции, производная дроби, производная логарифма.

  

Ответ:    .

Пример N 8

Вычислить производную функции    .

Решение.

Данная функция относится к виду показательно - степенной функции 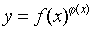 .  Для нахождения ее производной прологарифмируем данную функцию:    .

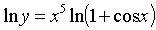Дифференцируя левую и правую часть этого равенства, получаем

  

Ответ:   . 

Тебе нравиться ы решения задач к разделу пределы? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое ы решения задач к разделу пределы, производная дифференциальое исчисление и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление

Из статьи мы узнали кратко, но содержательно про ы решения задач к разделу пределы