2.6.7. Производная по направлению, градиент

Привет, мой друг, тебе интересно узнать все про производная по направлению градиент, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое производная по направлению градиент , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.

Градиентом функции    в точке  M(x, y)  называется вектор с началом в точке  М, имеющий своими координатами частные производные функции  z,  . Для обозначения градиента часто используют символ  . Градиент указывает направление наибыстрейшего роста функции в данной точке.

Производной функции    в точке  M(x, y)  в направлении вектора    называется  .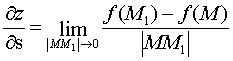

Если функция    дифференцируема, то производная в данном направлении вычисляется по формуле 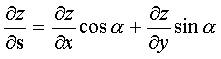 , где  α  - угол между вектором  s  и осью  OX.

Пользуясь определением градиента, формуле для производной по направлению можно придать вид:  , где вектор  s_o  - орт вектора  s, т.е. Об этом говорит сайт https://intellect.icu . производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления.

Производная 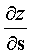   в направлении градиента имеет наибольшее значение, равное  .

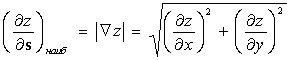Тебе нравиться производная по направлению градиент? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое производная по направлению градиент и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление