Лекция
Сразу хочу сказать, что здесь никакой воды про дифференциальные уравнения, и только нужная информация. Для того чтобы лучше понимать что такое дифференциальные уравнения , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Дифференциальное уравнение — уравнение, в которое входят производные функции и могут входить сама функция, независимая переменная и параметры. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или могут отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, 
не является дифференциальным уравнением
В отличие от алгебраических уравнений, в результате решения которых ищется число (несколько чисел), при решении дифференциальных уравнений ищется функция (семейство функций).
Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного дифференциального уравнения.
Современные быстродействующие ЭВМ эффективно дают численное решение обыкновенных дифференциальных уравнений, не требуя получения его решения в аналитическом виде. Это позволило некоторым исследователям утверждать, что решение задачи получено, если ее удалось свести к решению обыкновенного дифференциального уравнения.
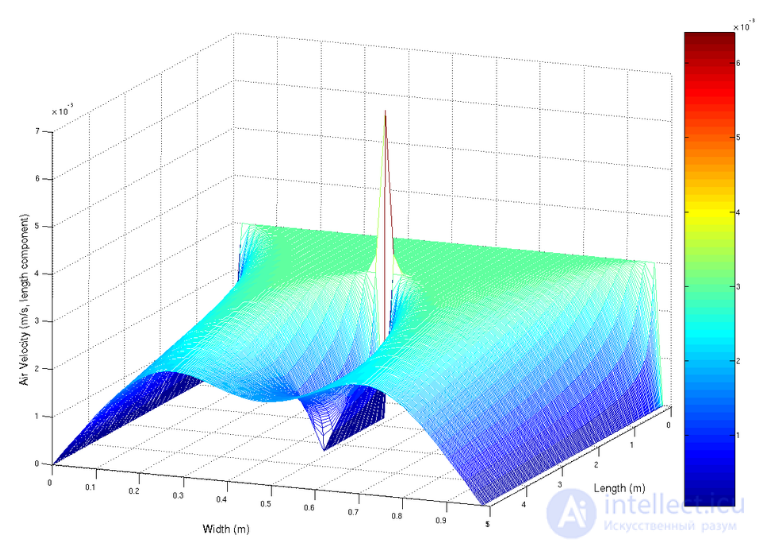
Визуализация воздушного потока, рассчитанная решением уравнения Навье-Стокса
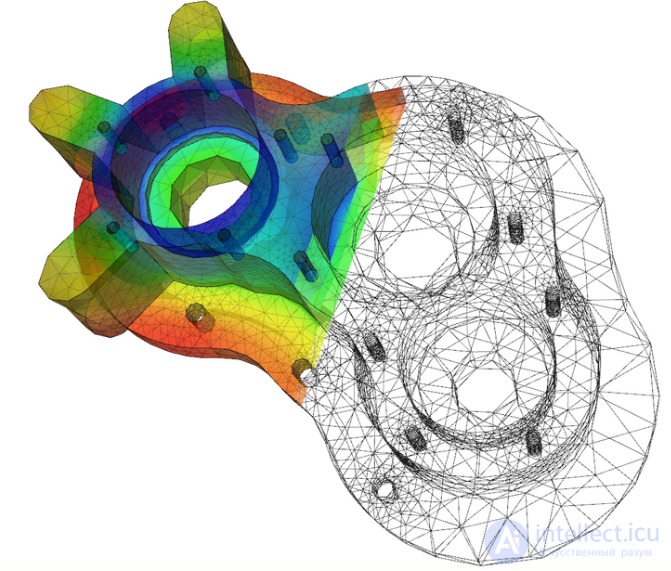
Визуализация теплообмена в корпусе насоса, созданная путем решения уравнения теплопроводности
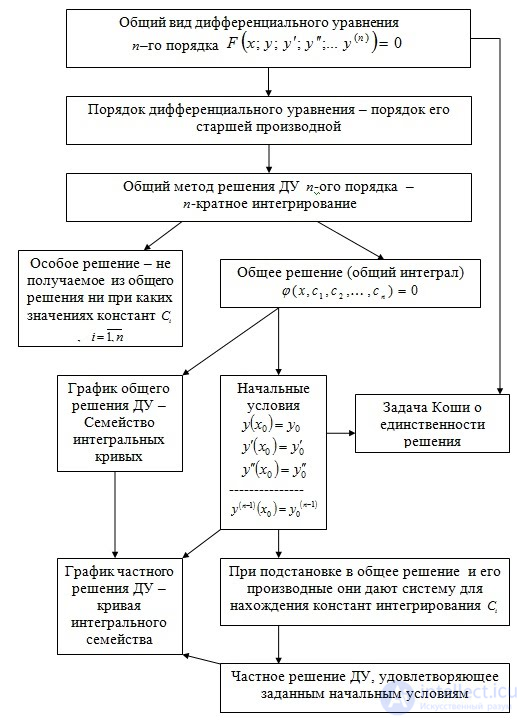
Порядок дифференциального уравнения — наивысший порядок производных, входящих в него интегралов.
Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется степенью дифференциального уравнения. Так, например, уравнение 
является уравнением второго порядка, четвертой степени .
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные 
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решенной, если нахождение неизвестной функции 
удается привести к квадратуре, (т. е. к виду 
, где 
— элементарная функция) независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных .
Важнейшим вопросом для дифференциальных уравнений является существование и единственность их решения. Разрешение этого вопроса дают теоремы существования и единственности, указывающие необходимые и достаточные для этого условия. Для обыкновенных дифференциальных уравнений такие условия были сформулированы Липшицем (1864). Для уравнений в частных производных соответствующая теорема была доказана С. В. Ковалевской (1874).
Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределенных функций решения становятся частными.
Поиск решений обыкновенных дифференциальных уравнений привел к установлению класса специальных функций — часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т. д.
Развитие теории дифференциальных уравнений позволило в ряде случаев отказаться от требования непрерывности исследуемых функций и ввести обобщенные решения дифференциальных уравнений.
Исаак Ньютон
Готфрид Лейбниц
Леонард Эйлер
Жозеф-Луи Лагранж
Пьер-Симон Лаплас
Жозеф Лиувилль
Анри Пуанкаре
Софья Ковалевская
Первоначально дифференциальные уравнения возникли из задач механики, в которых требовалось определить координаты тел, их скорости и ускорения, рассматриваемые как функции времени при различных воздействиях. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи.
Основой теории дифференциальных уравнений стало дифференциальное исчисление, созданное Лейбницем и Ньютоном (1642—1727). Сам термин «дифференциальное уравнение» был предложен в 1676 году Лейбницем.
Из огромного числа работ XVIII века по дифференциальным уравнениям выделяются работы Эйлера (1707—1783) и Лагранжа (1736—1813). В этих работах была прежде развита теория малых колебаний, а следовательно — теория линейных систем дифференциальных уравнений; попутно возникли основные понятия линейной алгебры (собственные числа и векторы в n-мерном случае). Вслед за Ньютоном Лаплас и Лагранж, а позже Гаусс (1777—1855) развивают также методы теории возмущений.
Когда была доказана неразрешимость алгебраических уравнений в радикалах, Жозеф Лиувилль (1809—1882) построил аналогичную теорию для дифференциальных уравнений, установив невозможность решения ряда уравнений (в частности таких классических, как линейные уравнения второго порядка) в элементарных функциях и квадратуре. Позже Софус Ли (1842—1899), анализируя вопрос об интегрировании уравнений в квадратурах, пришел к необходимости подробно исследовать группы диффеоморфизмов (получившие впоследствии имя групп Ли) — так по теории дифференциальных уравнений возникла одна из самых плодотворных областей современной математики, дальнейшее развитие которой было тесно связано совсем с другими вопросами (алгебры Ли еще раньше рассматривали Симеон-Дени Пуассон (1781—1840) и, особенно, Карл Густав Якоб Якоби (1804—1851)).
Новый этап развития теории дифференциальных уравнений начинается с работ Анри Пуанкаре (1854—1912), созданная им «качественная теория дифференциальных уравнений» вместе с теорией функций комплексных переменных легла в основу современной топологии. Качественная теория дифференциальных уравнений, или, как теперь ее чаще называют, теория динамических систем, сейчас активно развивается и имеет важные применения в естествознании.
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, зависящие от одной независимой переменной; они имеют вид
или 
где 
— неизвестная функция (возможно, вектор-функция; в таком случае часто говорят о системе дифференциальных уравнений), зависящая от независимой переменной {\displaystyle x,}
штрих означает дифференцирование по 
Число 
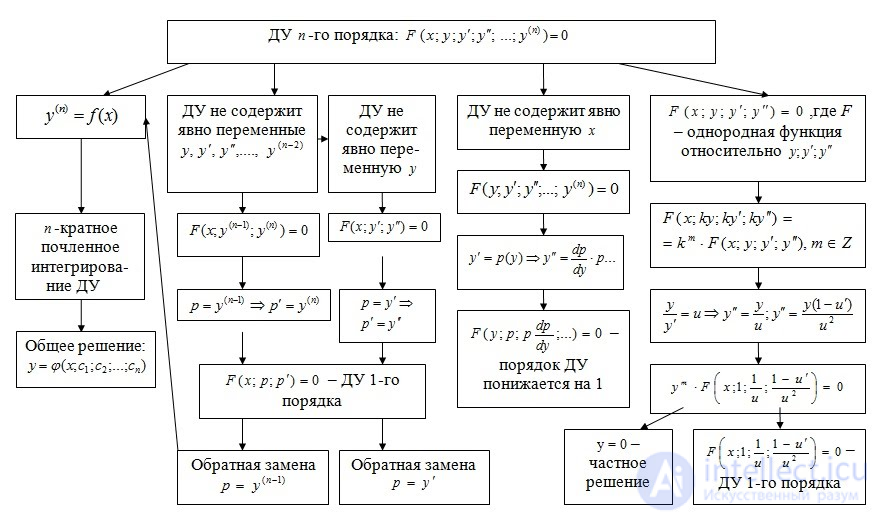
называется порядком дифференциального уравнения. Об этом говорит сайт https://intellect.icu . Наиболее практически важными являются дифференциальные уравнения первого и второго порядка.
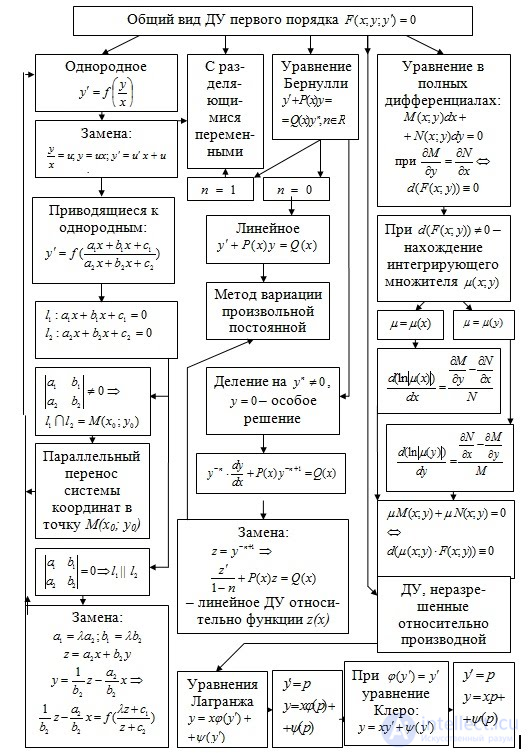
Простейшие дифференциальные уравнения первого порядка — класс дифференциальных уравнений первого порядка, наиболее легко поддающихся решению и исследованию. К нему относятся уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные уравнения первого порядка и линейные уравнения первого порядка. Все эти уравнения можно проинтегрировать в конечном виде.
Отправной точкой изложения будет служить дифференциальное уравнение первого порядка, записанное в т. н. симметричной форме:
где функции 
и 
определены и непрерывны в некоторой области 
.
Дифференциальные уравнения в частных производных (УРЧП) — это уравнения, содержащие неизвестные функции от нескольких переменных и их частные производные. Общий вид таких уравнений можно представить в виде:
где {\displaystyle x_{1},x_{2},\dots ,x_{m}}
— независимые переменные, а 
— функция этих переменных. Порядок уравнений в частных производных может определяется так же, как для обыкновенных дифференциальных уравнений. Еще одной важной классификацией уравнений в частных производных является их разделение на уравнения эллиптического, параболического и гиперболического типа, в особенности для уравнений второго порядка.
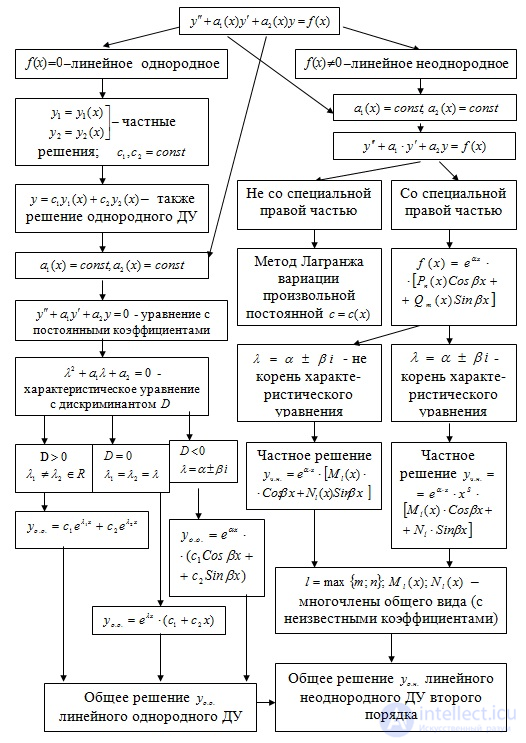
Как обыкновенные дифференциальные уравнения, так и уравнения в частных производных можно разделить на линейные и нелинейные. Дифференциальное уравнение является линейным, если неизвестная функция и ее производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Для таких уравнений решения образуют аффинное подпространство пространства функций. Теория линейных ДУ развита значительно глубже, чем теория нелинейных уравнений. Общий вид линейного дифференциального уравнения n-го порядка:
где pi(x) — известные функции независимой переменной, называемые коэффициентами уравнения. Функция r(x) в правой части называется свободным членом (единственное слагаемое, не зависящее от неизвестной функции). Важным частным классом линейных уравнений являются линейные дифференциальные уравнения с постоянными коэффициентами.
Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r(x) = 0. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
Нелинейные дифференциальные уравнения в общем случае не имеют разработанных методов решения, кроме некоторых частных классов. В некоторых случаях (с применением тех или иных приближений) они могут быть сведены к линейным. Например, линейное уравнение гармонического осциллятора {\displaystyle {\frac 
может рассматриваться как приближение нелинейного уравнения математического маятника 
для случая малых амплитуд, когда y ≈ sin y.
— однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением является семейство функций 
, где 
и 
— произвольные константы, которые для конкретного решения определяются из задаваемых отдельно начальных условий. Это уравнение, в частности, описывает движение гармонического осциллятора с циклической частотой 3.
где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.
Его решениями являются так называемые цилиндрические функции — функции Бесселя, Неймана, Ганкеля.
В следующей группе примеров неизвестная функция u зависит от двух переменных x и t или x и y.
— отклонение струны в точке с координатой x в момент времени t, а параметр a задает свойства струны: 
Некоторые дифференциальные уравнения имеют решения, что можно подать точной формуле. Такие классы уравнений представлены ниже.
В таблице, H ( x ), Z ( x ), H ( y ), Z ( y ) или H ( x , y ), Z ( x , y ) - произвольные интегрируемые функции от x или y (или от обоих параметров ), a A , B , C , I , L , N , M - константы. В общем A , B , C, I , L , являются действительными числами, а N , M , P и Q могут быть комплексными. Дифференциальные уравнения представлены в альтернативной форме, позволяющей их решить методом интегрирования.
| дифференциальные уравнения | общее решение | |
|---|---|---|
| 1 | 
|
 |
| 2 | 
|
 |
| 3 | 
|
 |
| 4 | 
|
 |
| 5 | } |
решением может быть скрытая Фунция от x и y , полученная вычислением приведенного интеграла используя замену переменных |
| 6 |  |
 |
|
Если ДР является точным, то есть 
тогда решение задается формулой: где Если уравнение не является точным, из функций H ( x , y ) и Z ( x , y ) можно определить интегральный множитель , после умножения уравнения на который оно решается аналогично точного. |
|
| 8 |  |
если тогда если тогда если тогда |
| 9 |  |
где |
Заметьте, что 3 и 4 являются частными случаями 7, они довольно распространены и представлены для полноты.
Также 8 уравнение является частным случаем 9, но 8 достаточно распространенная форма уравнений, особенно в простых физических и инженерных задачах.
,
где }
- масса тела, 
- его координата, 
- сила, действующая на тело с координатой в момент времени 
. Его решением является траектория движения тела под действием указанной силы.
,
где - отклонение струны в точке с координатой в момент времени , параметр 
задает свойства струны.
: 
,
где }
- вертикальные прогибы пластины, 
- цилиндрическая жесткость пластины при изгибе.
А как ты думаешь, при улучшении дифференциальные уравнения, будет лучше нам? Надеюсь, что теперь ты понял что такое дифференциальные уравнения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Математический анализ. Дифференциальное исчисление
и 
- определенные функции, зависящие от интегралов, позволяющие корректно определить функцию 
hold.
- d розвьзкы полинома степени d :
Комментарии
Оставить комментарий
Математический анализ. Дифференциальное исчисление
Термины: Математический анализ. Дифференциальное исчисление