Лекция
Привет, Вы узнаете о том , что такое логическая операция, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое логическая операция , настоятельно рекомендую прочитать все из категории Логика.
В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, с использованием уже существующих. В более узком смысле, понятие логической операции используется в математической логике и программировании.
В логике , А логическая связка (также называемый логический оператор , пропозициональной связкой , или сентенциальная оператор ) является логическим константа используется для соединения двух или более формул. Например , в синтаксисе из логики , в бинарной связке можно использовать для соединения двух атомарных формул
а также
, отображая сложную формулу
.
Общие связки включают отрицание , дизъюнкцию , союз и импликацию . В стандартных системах классической логики эти связки интерпретируются как функции истинности , хотя они получают множество альтернативных интерпретаций в неклассической логике . Их классические интерпретации аналогичны значениям выражений естественного языка, таких как английское «не», «или», «и», и «если», но не идентичны.композиционная семантика с устойчивой прагматикой .
Логическая связка похожа, но не эквивалентна синтаксису, обычно используемому в языках программирования, называемому условным оператором .
Логические операции с понятиями — такие мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
К операциям, которые связаны преимущественно с изменением содержания понятий, относятся:
К операциям, которые связаны преимущественно с объемами понятий, относятся:
Данные операции могут быть записаны математически с помощью теории множеств.
Переход же к математической логике связан с понятием суждений и установлением операций над ними с целью получения сложных суждений.
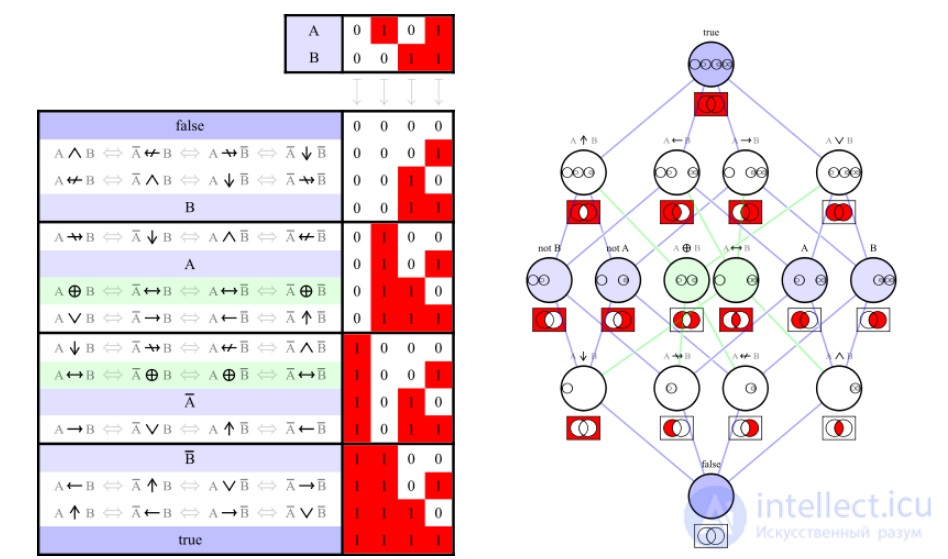
логическая операция (логический оператор, логическая связка, пропозициональная связка) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых .
В качестве основных обычно называют конъюнкцию ( или &), дизъюнкцию (
), импликацию (
), отрицание (
). В смысле классической логики логические связки могут быть определены через алгебру логики. В асинхронной секвенциальной логике определена логико-динамическая связка в виде операции венъюнкции (
).
Логическая операция — в программировании операция над выражениями логического (булевского) типа, соответствующая некоторой операции над высказываниями в алгебре логики. Как и высказывания, логические выражения могут принимать одно из двух истинностных значений — «истинно» или «ложно». Логические операции служат для получения сложных логических выражений из более простых. В свою очередь, логические выражения обычно используются как условия для управления последовательностью выполнения программы.
В некоторых языках программирования (например, в языке Си) вместо логического типа или одновременно с ним используются числовые типы. В этом случае считается, что отличное от нуля значение соответствует логической истине, а ноль — логической лжи.
Значение отдельного бита также можно рассматривать как логическое, если считать, что 1 означает «истинно», а 0 — «ложно». Это позволяет применять логические операции к отдельным битам, к битовым векторам покомпонентно и к числам в двоичном представлении поразрядно. Такое одновременное применение логической операции к последовательности битов осуществляется с помощью побитовых логических операций. Побитовые логические операции используются для оперирования отдельными битами или группами битов, применяются для наложения битовых масок, выполнения различных арифметических вычислений.
Среди логических операций наиболее известны конъюнкция (&&), дизъюнкция (||), отрицание (!). Их нередко путают с битовыми операциями, хотя это разные вещи. Например, следующий код на языке Си:
if (action_required && some_condition())
{
/* какие-то действия */
}
не выполнит вызов подпрограммы some_condition(), если значение логической переменной action_required ложно. Об этом говорит сайт https://intellect.icu . При такой операции второй аргумент операции «&&» вообще не будет вычислен.
В следующей таблице для некоторых языков программирования приведены встроенные операторы и функции, реализующие логические операции.
| Язык | НЕ | И | ИЛИ | Искл. ИЛИ | Эквив. | Не экв. | Другие |
|---|---|---|---|---|---|---|---|
| C++ | ! | && | || | ^ | == | != | |
| Fortran | .NOT. | .AND. | .OR. | .XOR. | .EQV. | .NEQV. | |
| Java | ! | && | || | ^ | == | != | |
| Pascal | not | and | or | xor | = | <> | |
| PL/I | ¬ | & | | | ¬ | = | ¬= | BOOL |
| ^ | ^ | ^= | |||||
| Prolog | \+ | , | ; | ||||
| Python | not | and | or | xor | == | != | |
| Turbo Basic | NOT | AND | OR | XOR | EQV | <> | IMP |
Стандартные логические связки классической логики имеют грубые эквиваленты в грамматиках естественных языков. В английском языке , как и во многих других языках, такие выражения обычно представляют собой грамматические союзы . Однако они также могут принимать форму дополнений , суффиксов глаголов и частиц . В денотатах естественных языка связок являются основной темой исследований в формальной семантике , поле , которое изучает логическую структуру естественных языков.
Значения связок естественного языка не совсем идентичны их ближайшим эквивалентам в классической логике. В частности, дизъюнкция может получить исключительную интерпретацию на многих языках. Некоторые исследователи приняли этот факт как доказательство того, что естественный язык семантика является неклассической . Однако другие поддерживают классическую семантику, постулируя прагматические объяснения исключительности, которые создают иллюзию неклассичности. В таких случаях исключительность обычно рассматривается как скалярная импликатура . Связанные головоломки, включающие дизъюнкцию, включают в себя выводы свободного выбора , ограничение Херфорда и вклад дизъюнкции вальтернативные вопросы .
Другие очевидные несоответствия между естественным языком и классической логикой включают парадоксы материального значения , анафору осла и проблему контрфактических условий . Эти явления были взяты в качестве мотивации для идентификации обозначений условных выражений естественного языка с логическими операторами, включая строгие условные , переменно строгие условные , а также различные динамические операторы.
В следующей таблице показаны стандартные классически определяемые приближения для английских связок.
| Английское слово | Соединительный | Символ | Логические ворота |
|---|---|---|---|
| нет | отрицание | "¬" | НЕТ |
| а также | соединение | "∧" | А ТАКЖЕ |
| или же | дизъюнкция | "∨" | ИЛИ ЖЕ |
| если ... то | материальное значение | «→» | ПОДРАЗУМЕВАТЬ |
| ...если | обратное следствие | «←» | |
| если и только если | двухусловный | "↔" | XNOR |
| не оба | альтернативное отрицание | «↑» | NAND |
| ни ни | совместное отрицание | «↓» | НИ |
| но нет | материальное непонимание | "↛" | ПРОСТО |
Некоторые логические связки обладают свойствами, которые могут быть выражены в теоремах, содержащих связку. Вот некоторые из свойств, которыми может обладать логическая связка:
Ассоциативность
В выражении, содержащем две или более одинаковых ассоциативных связки подряд, порядок операций не имеет значения, пока последовательность операндов не изменяется.
Коммутативность
Операнды связки можно поменять местами, сохраняя логическую эквивалентность исходному выражению.
Распределительность
Связка, обозначенная ·, распределяется по другой связке, обозначенной как +, если a · ( b + c ) = ( a · b ) + ( a · c ) для всех операндов a , b , c .
Идемпотентность
Когда операнды операции совпадают, соединение логически эквивалентно операнду.
Абсорбция
Пара связок ∧, ∨ удовлетворяет закону поглощения, если для всех операндов a , b .
Монотонность
Если f ( a 1 , ..., a n ) ≤ f ( b 1 , ..., b n ) для всех a 1 , ..., a n , b 1 , ..., b n ∈ {0 , 1} такие, что a 1 ≤ b 1 , a 2 ≤ b 2 , ..., a n ≤ b n . Например, ∨, ∧, ⊤, ⊥.
Близость
Каждая переменная всегда имеет значение для истинности операции или никогда не имеет значения. Например, ¬, ↔, , ⊤, ⊥.
Двойственность
Прочитать присвоение значений истинности для операции сверху вниз по ее таблице истинности - это то же самое, что выполнить дополнение к чтению таблицы той же или другой связки снизу вверх. Не прибегая к таблицам истинности, его можно сформулировать как g̃ (¬ a 1 , ..., ¬ a n ) = ¬ g ( a 1 , ..., a n ) . Например, ¬.
Сохраняющий правду
Составной частью всех этих аргументов являются тавтологии - это сама тавтология. Например, ∨, ∧, ⊤, →, ↔, ⊂ (см. Справедливость ).
Сохраняющий ложь
Все эти аргументы состоят в противоречиях, и это противоречие само по себе. Например, ∨, ∧,, ⊥, ⊄, ⊅ (см. Справедливость ).
Инволютивность (для унарных связок)
е ( е ( а )) = а . Например, отрицание в классической логике.
Для классической и интуиционистской логики символ «=» означает, что соответствующие импликации «… →…» и «… ←…» для логических соединений могут быть доказаны как теоремы, а символ «≤» означает, что «… →…» для логические соединения являются следствием соответствующих связок «… →…» для пропозициональных переменных. Некоторые многозначные логики могут иметь несовместимые определения эквивалентности и порядка (следствия).
И конъюнкция, и дизъюнкция ассоциативны, коммутативны и идемпотентны в классической логике, большинстве разновидностей многозначной логики и интуиционистской логике. То же верно и для распределения конъюнкции по дизъюнкции и дизъюнкции по конъюнкции, а также для закона поглощения.
В классической логике и некоторых разновидностях многозначной логики конъюнкция и дизъюнкция двойственны, а отрицание самодвойственно, последнее также самодвойственно в интуиционистской логике.
Чтобы уменьшить количество необходимых скобок, можно ввести правила приоритета : ¬ имеет более высокий приоритет, чем ∧, ∧ выше, чем ∨, и ∨ выше, чем →. Так, например, это сокращение от
.
Вот таблица, которая показывает обычно используемый приоритет логических операторов. [18]
Однако не все компиляторы используют один и тот же порядок; например, также использовался порядок, в котором дизъюнкция имеет более низкий приоритет, чем импликация или двойная импликация. [19] Иногда приоритет между соединением и дизъюнкцией не указан, и требуется указать его явно в данной формуле с круглыми скобками. Порядок приоритета определяет, какая связка является «основной связкой» при интерпретации неатомарной формулы.
Функциональный подход к логическим операторам реализован в виде логических вентилей в цифровых схемах . Практически все цифровые схемы (главным исключением является DRAM ) построены из NAND , NOR , NOT и шлюзов передачи ; более подробную информацию см. в разделе « Функция истины в информатике» . Логические операторы над битовыми векторами (соответствующие конечным булевым алгебрам ) являются побитовыми операциями .
Но не каждое использование логической связки в компьютерном программировании имеет булеву семантику. Например, ленивое вычисление иногда реализуется для P ∧ Q и P ∨ Q , поэтому эти связки не коммутативны, если одно или оба выражения P , Q имеют побочные эффекты . Кроме того, условное выражение , которое в некотором смысле соответствует материальной условной связке, по существу не является логическим, потому что для if (P) then Q;, консеквент Q не выполняется, если антецедент P является ложным (хотя соединение в целом является успешным - «истина» в таком случае). Это ближе к интуиционистским и конструктивистским взглядам на материальные условности, а не к взглядам классической логики.
Исследование, описанное в статье про логическая операция, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое логическая операция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Логика
Термины: Логика