Лекция
Привет, Вы узнаете о том , что такое законы логики, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое законы логики, закон тождества, закон контрапозиции, законы де моргана, модус, поненс, толленс, утверждающе-отрицающий модус, отрицающе-утверждающий модус, конструктивная дилемма, деструктивная дилемма, закон клавия, дилемма, правила де моргана, законы де моргана, закон де моргана, доказательство по случаям , настоятельно рекомендую прочитать все из категории Логика.
Законы двойного отрицания позволяют снимать и вводить такое отрицание. Их можно выразить так:если неверно, что не-А, то А; если А, то неверно, что не-А.Например: «Если неверно, что Аристотель не знал закона двойного отрицания, то Аристотель знал этот закон» и наоборот.
Закон тождества — принцип постоянства или принцип сохранности предметного и смыслового значений суждений (высказываний) в некотором заведомо известном или подразумеваемом контексте (в выводе, доказательстве, теории) . Является одним из законов классической логики.
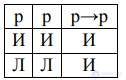
Рис 1 Закон тождества
Согласно закону тождества, всякое высказывание об одном и том же предмете в одно и то же время и в одном и том же отношении должно быть тождественно самому себе, сколько бы раз не воспроизводилось. Закон тождества может быть выражен формулой p→p (рис. 1).
Самый простой из всех логических законов — это, пожалуй, закон тождества. Он говорит: если утверждение истинно, то оно истинно, «если А, то А». Например, если Земля вращается, то она вращается, и т.п. Чистое утверждение тождества кажется настолько бессодержательным, что редко кем употребляется.
Древнекитайский философ Конфуций поучал своего ученика: «То, что знаешь, считай, что знаешь, то, что не знаешь, считай, что не знаешь». Здесь не просто повторение одного и того же: знать что-либо и знать, что это знаешь, не одно и то же.
Закон тождества кажется в высшей степени простым и очевидным. Однако и его ухитрялись истолковывать неправильно. Заявлялось, например, будто этот закон утверждает, что вещи всегда остаются неизменными, тождественными самим себе. Это, конечно, недоразумение. Закон ничего не говорит об изменчивости или неизменности. Он утверждает только, что если вещь меняется, то она меняется, а если она остается одной и той же, то она остается той же.
В процессе рассуждения каждое понятие, суждение должно употребляться в одном и том же смысле. Предпосылкой этого является возможность различения и отождествления тех объектов, о которых идет речь. . Мысль о предмете должна иметь определенное, устойчивое содержание, сколько бы раз она ни повторялась. Важнейшее свойство мышления — его определенность — выражается данным логическим законом .
Впервые закон тождества сформулирован Аристотелем в трактате «Метафизика» следующим образом:
«…иметь не одно значение — значит не иметь ни одного значения; если же у слов нет значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности — и с самим собой; ибо невозможно ничего мыслить, если не мыслить что-нибудь одно»
— Аристотель, «Метафизика»
В формальной логике закон тождества принято выражать формулой: есть
, или
, где под
понимается любая мысль.
Символическая логика при построении исчислений высказываний оперирует формулами (читается как «
влечет
») и
≡
(читается как «
равнозначно
»), где:
Эти формулы соответствуют закону тождества.
В логике предикатов закон тождества выражается формулой , то есть для всякого
верно, что если
имеет свойство
, то
имеет это свойство.
Любой наш знакомый изменяется с каждым годом, но мы все же отличаем его от других знакомых и незнакомых нам людей (имеется возможность различения), потому что он сохраняет основные черты, которые выступают как те же самые на всем протяжении жизни нашего знакомого (имеется возможность отождествления). То есть, в соответствии с законом Лейбница (определяющим понятие тождество) мы утверждаем, что наш знакомый изменился. Однако в соответствии с законом тождества мы утверждаем, что это один и тот же человек, поскольку в основе определения лежит понятие личность. Закон тождества требует, чтобы для описания одного и того же понятия мы всегда использовали одно и то же выражение (имя). Таким образом, мы одновременно рассматриваем один объект (знакомого) на двух различных уровнях абстракции. Возможность различения и отождествления определяется в соответствии с законом достаточного основания. В данном случае в качестве достаточного основания используется наше чувственное восприятие (см. опознание).
Под тождественностью мысли самой себе в формальной логике понимается тождественность ее объема . Это означает, что вместо логической переменной в формулу «
есть
» могут быть подставлены мысли различного конкретного содержания, если они имеют один и тот же объем. Вместо первого
в формуле «
есть
» мы можем подставить понятие «животное; обладающее мягкой мочкой уха», а вместо второго — понятие «животное, обладающее способностью производить орудия труда» (обе эти мысли с точки зрения формальной логики считаются равнозначными, неразличимыми, так как они имеют один и тот же объем, а именно — признаки, отраженные в этих понятиях, относятся лишь к классу людей), и при этом получается истинное суждение «Животное, обладающее мягкой мочкой уха, есть животное, обладающее способностью производить орудия труда».
В математической логике законом тождества называется тождественно истинная импликация логической переменной с самой собой .
В алгебре понятие арифметического равенства чисел рассматривается как особый случай общего понятия логического тождества. Однако имеются математики, которые, в противоположность данной точке зрения, не отождествляют символа «», встречающегося в арифметике, с символом логического тождества; они не считают, что равные числа непременно тождественны, и поэтому рассматривают понятие числового равенства как специфически арифметическое понятие. То есть полагают, что сам факт наличия или отсутствия особого случая логического тождества, должен определяться в рамках логики.[10].
Когда закон тождества нарушается непроизвольно, по незнанию, тогда возникают логические ошибки, которые называются паралогизмами; но когда этот закон нарушается преднамеренно, с целью запутать собеседника и доказать ему какую-нибудь ложную мысль, тогда появляются ошибки, называемые софизмами .
При нарушении закона тождества возможны следующие ошибки:
«Закон контрапозиции» — это общее название для ряда логических законов, позволяющих с помощью отрицания менять местами основание и следствие условного высказывания.
Закон контрапозиции — закон классической логики, утверждающий, что в том случае, если некая посылка A влечет некое следствие B, то отрицание этого следствия (то есть «не B») влечет отрицание этой посылки (то есть «не A»).
Как и всякое общезначимое импликативное утверждение, может служить также и правилом вывода.
В виде формулы алгебры высказываний закон контрапозиции имеет вид . Также являются тавтологиями следующие похожие формулы:
,
. При подстановке вместо
произвольных формул также получаются тавтологии.
Закон контрапозиции доказуем в исчислении высказываний, но при этом формула невыводима в интуиционистском исчислении высказываний, где p, q - пропозициональные переменные.
Один из этих законов, называемый иногда законом простой контрапозиции, звучит так: если первое влечет второе, то отрицание второго влечет отрицание первого.
Например: «Если верно, что число, делящееся на шесть, делится на три, то верно, что число, не делящееся на три, не делится на шесть».
Другой закон контрапозиции говорит: если верно, что если не-первое, то не-второе, то верно, что если второе, то первое.
Например: «Если верно, что рукопись, не получившая положительного отзыва, не публикуется, то верно, что публикуемая рукопись имеет положительный отзыв». Или другой пример: «Если нет дыма, когда нет огня, то если есть огонь, есть и дым».
Еще два закона контрапозиции:
• если дело обстоит так, что если Л, то не-В, то если В, то не-А, например: «Если квадрат не является треугольником, то треугольник не квадрат»;
• если верно, что если не-А, то В, то если не-В, то А; например: «Если не являющееся очевидным сомнительно, то не являющееся сомнительным очевидно».
Законы де Моргана ( правила де моргана ) — логические правила, связывающие пары логических операций при помощи логического отрицания. Названы в честь шотландского математика Огастеса де Моргана. В краткой форме звучат так:
Отрицание конъюнкции есть дизъюнкция отрицаний.
Отрицание дизъюнкции есть конъюнкция отрицаний.
«Противоречащая противоположность дизъюнктивного суждения — конъюнктивное суждение, составленное из противоречащих противоположностей частей дизъюнктивного суждения (The contradictory opposite of a disjunctive proposition is a conjunctive proposition composed of the contradictories of the parts of the disjunctive proposition)» (Уильям Оккам, Summa Logicae).
Именем английского логика XIX в. А. де Моргана называются логические законы, связывающие с помощью отрицания высказывания образованные с помощью союзов «и» или «или». Один из этих законов можно выразить так: отрицание высказывания «Л и В» эквивалентно высказыванию «не-А илине-В».
Другой закон: неверно, что Ли В если и только если неверно Л и неверно В. 11апример: «Неверно, что ученик знает арифметику или знает геометрию, если и только если он не знает ни арифметики, ни геометрии».
На основе этих законов, используя отрицание, связку «и» можно определить через «или», и наоборот:
«А и В» означает «неверно, что не-А или не-В»,
«А и В» означает «неверно, что не-А и не-В».
Например: «Идет дождь и идет снег» означает «Неверно, что нет дождя или нет снега»; «Сегодня холодно или сыро» означает «Неверно, что сегодня не холодно и не сыро».
Огастес де Морган первоначально заметил, что в классической пропозициональной логике справедливы следующие соотношения:
не (a и b) = (не a) или (не b)
не (a или b) = (не a) и (не b)
В математике это выглядит так:
или по-другому:
В теории множеств:
или по-другому:
Эти правила также действительны для множества элементов (семейств):
и
.
В исчислении предикатов:
Следствия:
Используя законы де Моргана, можно выразить конъюнкцию через дизъюнкцию и три отрицания. Об этом говорит сайт https://intellect.icu . Аналогично можно выразить дизъюнкцию:
В виде теоремы:
Если существует суждение, выраженное операцией логического умножения двух или более элементов, т. е. операцией «и»: , то для того, чтобы найти обратное
от всего суждения, необходимо найти обратное от каждого элемента и объединить их операцией логического сложения, т. е. операцией «или»:
. Закон работает аналогично в обратном направлении:
.
Законы де Моргана применяются в таких важных областях, как дискретная математика, электротехника, физика и информатика; например, используются для оптимизации цифровых схем посредством замены одних логических элементов другими.
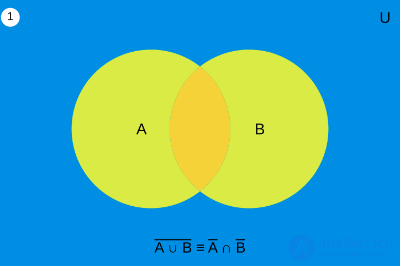
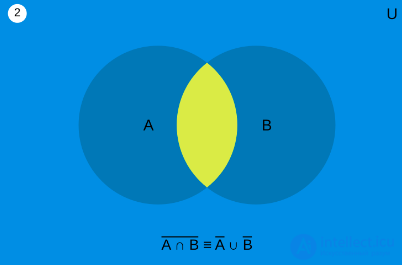
Диаграммы Венна, описывающие законы де Моргана
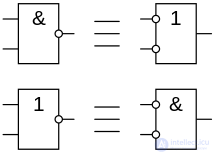
Представление правил де Моргана через логические элементы
«Модусом» в логике называется разновидность некоторой общей формы рассуждения. Далее будут перечислены четыре близких друг другу модуса, известных еще средневековым логикам.
Modus ponens («правило вывода»): если и
— выводимые формулы, то
также выводима.
Форма записи: , где
— любые формулы.
Правило вывода модус поненс, обычно называемое правилом отделения или гипотетическим силлогизмом, позволяет от утверждения условного высказывания и утверждения его основания
(антецедента) перейти к утверждению следствия
(консеквента). Например, металлы — проводники тока, цинк — металл, значит цинк проводит ток. Обратное утверждение не всегда верно: никель и морская вода проводят ток, но никель — металл, а морская вода не металл. Итого, если из
следует
, и
— истинно, то
может быть как истинно, так и ложно.
Modus ponens — правило вывода в исчислении высказываний. Является частным случаем правила резолюций.
Модус поненс, называемый иногда гипотетическим силлогизмом, позволяет от утверждения условного высказывания и утверждения его основания перейти к утверждению следствия этого высказывания:

Здесь высказывания «если А, то В» и «А» — посылки, высказывание «В» заключение.
Горизонтальная черта стоит вместо слова «следовательно».
Другая запись: Если А, то В. А. Следовательно, В.
Благодаря этому модусу от посылки «если А, то В», используя посылку «А», мы как бы отделяем заключение «В». На этом основании данный модус иногда называется «правилом отделения».
Например: Если у человека диабет, он болен. У человека диабет. Человек болен.
Рассуждение по правилу отделения идет от утверждения основания истинного условного высказывания к утверждению его следствия. Это логически корректное движение мысли иногда путается со сходным, но логически неправильным ее движением от утверждения следствия истинного условного высказывания к утверждению его основания.
Например, правильным является умозаключение:
Но внешне сходное с ним умозаключение:
Если бы электролит был металлом, он проводил бы электрический ток. Электролит проводит электрический ток.
Электролит — металл логически некорректно. Рассуждая по последней схеме, можно прийти от истинных посылок к ложному заключению. Против смешения правила отделения с этой неправильной схемой рассуждения предостерегает совет: от подтверждения основания к подтверждению следствия рассуждать допустимо, от подтверждения следствия к подтверждению основания — нет.
Modus tollens — рассуждение от противного (латинское «modus tollendo tollens» означает «путь исключения исключением»).
Форма записи: .
Например, — «золотая монета»,
— «несминаема зубами» , тогда modus tollens позволяет из свойства: «золотые монеты несминаемы зубами» сделать вывод, что если монета сминаема зубами, то она не золотая.
Модусом толленсом называется следующая схема рассуждения:
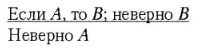
Здесь высказывания «если A, то В» и «неверно В» являются посылками, а высказывание «неверно A» — заключением. Другая запись:
Если А, то В. Не-В. Следовательно, не-А.
Посредством этой схемы от утверждения условного высказывания и отрицания его следствия осуществляется переход к отрицанию основания. Например: «Если гелий — металл, он электропроводен. Гелий неэлектропроводен. Следовательно, гелий — не металл».
По схеме модус толленс идет процесс фальсификации, установления ложности теории или гипотезы в результате ее эмпирической проверки. Из проверяемой теории T выводится некоторое эмпирическое утверждение A, т.е. устанавливается условное высказывание «если T, то A». Посредством эмпирических методов познания (наблюдения, измерения или эксперимента) предложение A сопоставляется с реальным положением дел.
Выясняется, что A ложно и истинно предложение не-А.Из посылок «если T то A» и «не-А» следует «не-T», т.е. ложность теории T".
С модусом толленсом нередко смешивается внешне сходное с ним умозаключение:
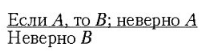
В последнем умозаключении от утверждения условного высказывания и отрицания его основания осуществляется переход к отрицанию его следствия, что является логически некорректным шагом. Рассуждение по такой схеме может привести от истинных посылок к ложному заключению.
Например:
Все металлы пластичны, и если бы глина была металлом, она также являлась бы пластичной. Однако глина не является металлом. Но из этого очевидным образом не вытекает, что глина не пластична. Кроме металлов, есть и другие пластичные вещества, и глина в их числе.
Против смешения модуса толленса с данной некорректной схемой рассуждения предостерегает совет: от отрицания следствия условного высказывания заключать к отрицанию основания этого высказывания можно, а от отрицания основания к отрицанию следствия — нет.
В утверждающе‑отрицающем модусе (modus ponendo tollens) меньшая посылка, категорическое суждение, утверждает один член дизъюнкции, заключение – также категорическое суждение – отрицает другой ее член. Напр.: Облигации могут быть предъявительскими (р) или именными (q).
Данная облигация предъявительская (p). Данная облигация не является именной (q).
Схема утверждающе-отрицающего модуса:
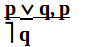
Заключение по этому модусу всегда достоверно, если соблюдается правило: большая посылка должна быть исключающе-раздели-тельным суждением, или суждением строгой дизъюнкции. Если это правило не соблюдается, достоверного заключения получить нельзя. В самом деле, из посылок «Кражу совершил К. или Л.» и «Кража совершена К.» заключение «Л. кражу не совершал» с необходимостью не следует. Возможно, что Л. также причастен к совершению кражи, является соучастником К.
Утверждающе-отрицающим модусом именуются следующие схемы рассуждения:
Либо А. либо В: А
Неверно В
и
Либо А. либо В: В
Неверно А
Другая запись:
Либо А, либо В. А.Следовательно, не-В.
Либо А, либо В. В. Следовательно, не-А.
Посредством этих схем от утверждения двух взаимоисключающих альтернатив и установления того, какая из них имеет место, осуществляется переход к отрицанию второй альтернативы: либо первое, либо второе, но не оба вместе; есть первое; значит, нет второго. Например:
Лермонтов родился в Москве либо в Петербурге. Он родился в Москве.
Неверно, что Лермонтов родился в Петербурге.

Связка «либо, либо», входящая в утверждающе-отрицающий модус , является исключающей, она означает: истинно первое или истинно второе, но не оба вместе. Такое же рассуждение, но с неисключающим «или» (имеет место первое или второе, но возможно, что и первое и второе) логически неправильно. От истинных посылок оно может вести к ложному заключению. Например:
На Южном полюсе был Амундсен или был Скотт. Па Южном полюсе был Амундсен.
Неверно, что там был Скотт.
Обе посылки истинны: и Амундсен, и Скотт достигли Южного полюса, заключение же ложно. Правильным является умозаключение:
На Южном полюсе первым был Амундсен или Скотт. На этом полюсе первым был Амундсен.
Неверно, что там первым был Скотт.

В отрицающе‑утверждающем модусе (modus tollendo ponens) меньшая посылка отрицает один дизъюнкт, заключение утверждает другой. Напр.: Облигации могут быть предъявительскими (р) или именными (q). Данная облигация не является предъявительской (⌉р). Данная облигация именная (q).
Схема отрицающе-утверждающего модуса:
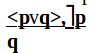
Утвердительный вывод получен посредством отрицания: отрицая один дизъюнкт, мы утверждаем другой.
Заключение по этому модусу всегда достоверно, если соблюдается правило: в большей посылке должны быть перечислены все возможные суждения — дизъюнкты, иначе говоря, большая посылка должна быть полным (закрытым) дизъюнктивным высказыванием.
Отрицающе-утверждающим модусом называется разделительно-категорическое умозаключение: первое или второе; не-первое; значит, второе. Первая посылка — высказывание с «или»; вторая — категорическое высказывание, отрицающее один из членов первого сложного высказывания; заключением является второй член этого высказывания.
А или В: неверно А
В
или
А или В; неверно В
А
Другая форма записи:
А или В. Не-А. Следовательно, В.
А или В. Не-В. Следовательно, А.
Например:
Множество является конечным или оно бесконечно. Множество не является конечным.
Множество бесконечно.
Средневековые логики называли утверждающе-отрицающий модус модусом понендо толленс, а отрицающе-утверждающий модус — модусом толлендо поненс.
дилемма ми называются рассуждения, посылками которых являются, по меньшей мере, два условных высказывания (высказывания с «если, то») и одно разделительное высказывание (высказывание с «или»).
Дилемма - это условно-категорическое УМЗ, где одна посылка состоит из 2-х или более условных суждений, а другая является разделительным суждением и если разделительное суждение содержит 2 члена.
Простая конструктивная дилемма - состоит из 2-х посылок. В 1-й утверждается, что из 2-х разных оснований вытекает одно следствие. Во 2-й утверждаются, что оба этих основания истинны. В заключении утверждается следствие. “Если я пойду по мосту - меня заметят. Если я пойду вброд - меня заметят. Я могу идти по мосту или вброд. Меня заметят. “.
Сложная конструктивная дилемма. Два основания в 1-й посылке, во 2-й посылке утверждается истинность одного или другого основания, в заключении утверждается истинность одного или другого следствия. “Если я ебну бомбу в городе, то завалю много народа. Если я ебну бомбу в лесу, то завалю себя одного. Я могу ебнуть бомбу в городе и в лесу. Я могу завалить много народа или я могу убить только себя.”. Простая деструктивная дилемма - 1-я условная посылка указывает на то, что из одного и того же основания вытекают 2 различных следствия, 2-я посылка это отрицания обоих этих следствий, а в заключении отрицается основание. “Если у человека столбняк, то через 1 день он сдохнет. Через один день человек не сдох. У этого человека нет столбняка”.
Сложная деструктивная дилемма - 1 посылка состоит из 2-х условных суждений с разными основаниями и разными следствиями, 2-я посылка - это отрицание обоих следствий. “Если Петров честен, он сделает задание сегодня, а если Петров добросовестен, то он сделает задание завтра. Но Петров не сделал задание сегодня и не сделал его завтра. Петров не честен и не добросовестен.
Выделяются следующие разновидности дилеммы.
Простая конструктивная (утверждающая) дилемма:
Если А, то С.
Если В, то С.
А или В.
С
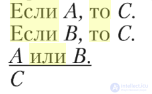
Рассуждение этого типа в математике принято называть доказательством по случаям. Однако число случаев, перебираемых последовательно в математическом доказательстве, обычно превышает два, так что дилемма приобретает вид:
Если бы было справедливо первое допущение, теорема была бы верна; при справедливости второго допущения теорема также была бы верна; при верном третьем допущении теорема верна; если верно четвертое допущение, теорема верна; справедливо или первое, или второе, или третье, или четвертое допущение.
Значит, теорема верна.
Сложная конструктивная дилемма :
Если А, то В. Если С, то D.
A или С.
В или D.

Например: «Если будет дождь, мы пойдем в кино; если будет холодно, пойдем в театр; будет дождь или будет холодно; следовательно, мы пойдем в кино или пойдем в театр».
Простая деструктивная (отрицающая) дилемма:
Если А, то В. Если А, то С.
Неверно В или неверно С. Неверно А.
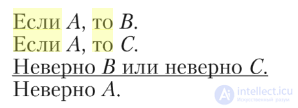
Например: «Если число делится на 6, то оно делится на 3; если число делится на б, то оно делится на 2; рассматриваемое число не делится на 2 или не делится па 3; следовательно, число не делится на 6».
Сложная деструктивная дилемма :
Если А, то В. Если С, то D. Не-В или не-Р. Не-А или не-С.
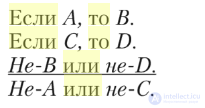
Например: «Если поеду на север, то попаду в Тверь; если поеду на юг, то попаду в Тулу; но не буду в Твери или не буду в Туле; следовательно, не поеду на север или не поеду на юг».
Этот закон можно передать так: если из отрицания некоторого высказывания вытекает само это высказывание, то оно является истинным. Или, короче: высказывание, вытекающее из своего собственного отрицания, истинно.

Если неверно, что А.то А.
А.
Например: если условием того, чтобы машина не работала, является ее работа, то машина работает.
Закон назван именем Клавия — ученого-иезуита, жившего в XVI в., одного из создателей григорианского календаря. Клавий обратил внимание на этот закон в своем комментарии к «Началам» Евклида. Одну из своих теорем Евклид доказал из допущения, что она является ложной.
Закон Клавия лежит в основе рекомендации, касающейся доказательства: если хочешь доказать А,выводи А из допущения, что верным является не-А. Например, нужно доказать утверждение «Трапеция имеет четыре стороны». Отрицание этого утверждения: «Неверно, что трапеция имеет четыре стороны». Если из этого отрицания удается вывести утверждение, то последнее будет истинно.
В романе И. С. Тургенева «Рудин» есть такой диалог:
— Стало быть, по-вашему, убеждений пет?
— Нет — и не существует.
— Это ваше убеждение? -Да.
- Как же вы говорите, что их нет? Вот вам уже одно на первый случай.
Ошибочному мнению, что никаких убеждений нет, противопоставляется его отрицание: есть, по меньшей мере, одно убеждение, а именно убеждение, что убеждений нет. Отсюда следует, что убеждения существуют.
К закону Клавия близок по своей логической структуре другой закон, отвечающий этой же общей схеме: если из утверждения вытекает его отрицание, то последнее истинно. Например, сети условием того, что поезд придет вовремя, будет его опоздание, то поезд опоздает.
Схема этого рассуждения :
Если А. то не-А.
Не-А.
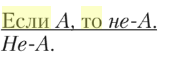
Эту схему однажды использовал древнегреческий философ Демокрит в споре с софистом Протагором. Последний утверждал:
«Истинно все то, что кому-либо приходит в голову».
На это Демокрит ответил, что из положения
«Каждое высказывание истинно» вытекает истинность и его отрицания: «Не все высказывания истинны».
И значит, это отрицание, а не положение Протагора на самом деле истинно.
1. Опираясь на закон тождества, установите, в каком случае сохраняется тождество суждений, если выделенное понятие заменить другим: Преступник, скрываясь от преследования, свернул в безлюдный переулок.
2. Закон противоречия нарушен в следующем высказывании:
Закон противоречия гласит: два высказывания, находящиеся в отношении отрицания, не могут быть одновременно истинными, по крайней мере одно из них ложно. Для того чтобы закон противоречия действовал, надо рассуждать об одном и том же предмете, в одно и то же время в одном и том же отношении. Закон противоречия может быть выражен формулой ┐(pר┐p) (рис. 2)
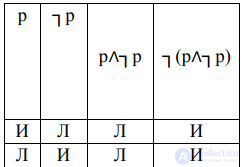
рис 2 Закон противоречия
3. В этом шуточном четверостишии
Мы ходили по Неглинной,
Заходили на бульвар,
Нам купили синий-синий,
Презеленый, красный шар.
(С.В. Михалков)
преднамеренно нарушен закон
4. Два противоположных суждения о двух разных предметах
5. Два противоречащих суждения об одном предмете предметах должны быть
6. Опираясь на закон непротиворечия и исключенного третьего, установите, какие из пар суждений могут быть одновременно ложными.
Закон исключенного третьего: два противоречащих друг другу высказывания не могут быть ни одновременно истинными, ни одновременно ложными, одно из них истинно, другое – ложно, третьего не дано. Закон исключенного третьего в виде формулы записывается следующим образом: pڀ┐p (рис. 3).
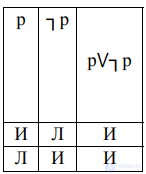
Рис 3 Закон исключенного третьего
7. Укажите, какой из формальных законов логики нарушен в следующем рассуждении: «Этот человек не болен, ведь у него не повышена температура».
1. Определите, являются ли высказываниями следующие предложения:
2. Определите вид простого высказывания по характеру предиката.
3. Запишите высказывания в правильной логической форме, выделите субъект и предикат.
4. Определите вид атрибутивного высказывания по качеству и количеству, установите субъект, предикат, связку и кванторное слово.
5. Определите вид атрибутивного высказывания по объединенной классификации, установите субъект и предикат, изобразите отношения
между терминами при помощи круговых схем, установите распределенность терминов в высказывании.
6. Подберите собственные примеры общеутвердительных, частноутвердительных, общеотрицательных и частноотрицательных высказываний.
7. Составьте высказывания с предложенными субъектом и предикатом в соответствии со следующими условиями распределенности терминов:
а) S- P+; б) S+ P+; в) S- P-; г) S+ P- и скажите, какие из полученных высказываний истинные, а какие – ложные:
8. В значении каких логических союзов употреблены следующие грамматические союзы:
9. Переведите сложные высказывания на язык логики.
10. Формализуйте следующие рассуждения.
11. Постройте таблицы истинности для следующих формул и определите тип формулы (тождественно-истинная, тождественно-ложная, нейтральная):
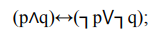
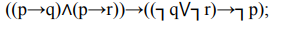
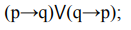
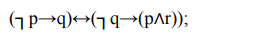
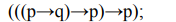
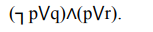
12. Преобразуйте следующие простые высказывания с внешним отрицанием в высказывания без внешнего отрицания.
13. Даны высказывания. Опираясь на логический квадрат, выведите высказывания, подчиняющее, подпротивное и противоречащее исходному.
Установите истинность выведенных высказываний, если по условию исходное высказывание – истинно.
14. Дана пара высказываний.
Ответьте на следующие вопросы:
15. Проверьте правильность рассуждений, построенных на основе «логического квадрата», укажите, в каких примерах допущены ошибки и в
чем они заключаются.
16. Являются ли равнозначными следующие пары высказываний (если нет, установите вид отношений между их логическими формами)?
17. Найдите среди перечисленных сложных высказываний противоречащие и эквивалентные.
18. С помощью таблиц истинности установите, соответствуют ли логическим законам следующие рассуждения:
19. Какой из основных законов мышления нарушен?
20. Анекдоты основаны на нарушении основных логических законов.
Например:
Студенты решают, что им делать накануне экзамена. Решают бросить монету.
Требования какого закона нарушаются в этом анекдоте? Если можете, приведите свои примеры
Чисто условное умозаключение
В общем, мой друг ты одолел чтение этой статьи об законы логики. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое законы логики, закон тождества, закон контрапозиции, законы де моргана, модус, поненс, толленс, утверждающе-отрицающий модус, отрицающе-утверждающий модус, конструктивная дилемма, деструктивная дилемма, закон клавия, дилемма, правила де моргана, законы де моргана, закон де моргана, доказательство по случаям и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Логика
Термины: Логика