Лекция
Сразу хочу сказать, что здесь никакой воды про суждение, и только нужная информация. Для того чтобы лучше понимать что такое суждение, абстрактная мысль , настоятельно рекомендую прочитать все из категории Логика.
суждение - это абстрактная мысль , в которой что-либо утверждается или отрицается. Схема простого суждения выглядит так: S есть (не есть) Р, где S - субъект суждения, т.е. логическое подлежащее, то, о чем судят, Р - предикат суждения, т.е. логическое сказуемое, то, что присуждается субъекту. Строго говоря, связка "быть" с отрицанием или без него тоже входит в состав предиката, но, чтобы показать, что простое суждение - это отношение двух понятий, одно из которых играет роль субъекта, а другое - предиката, связку преподносят как самостоятельный элемент формы.
Суждения делят на виды по качеству и количеству. Качеством простого суждения называется его утвердительность или отрицательность. Его количество определяется по характеру субъекта. Если судят о чем-то единичном, суждение называют единичным, если о любом элементе какого-то множества - общим, если о части элементов множества - частным. Единичные и общие суждения часто объединяют в один вид, рассуждая примерно так: разница между первыми и вторыми всего лишь в том, что в первых множество, о котором судят, состоит из единственного элемента. Оставив всего два вида по количеству (единичные плюс общие, с одной стороны, и частные - с другой), проводят объединенное деление простых суждений по количеству и качеству и получают четыре вида категорических суждений.

Логический квадрат
Знакомиться с видами категорических суждений удобно с помощью так называемого "логического квадрата": надо нарисовать квадрат, а в вершинах его поставить латинские буквы A, E, I и O, которыми обозначаются виды суждений. Чтобы легче было запомнить эти буквенные обозначения, слева от квадрата следует написать латинское слово "affirmo" ("утверждаю"), а справа - "nego" ("отрицаю"). Расположение этих слов не случайно. Дело в том, что в левой части квадрата размещаются буквы для двух видов утвердительных суждений, а в правой части - для двух видов отрицательных. При этом в верхней части квадрата записывают виды общих плюс единичных суждений, а в нижней - частных.
Поскольку первая гласная в каждом из указанных латинских слов дает буквенное обозначение общему (единичному) суждению, а вторая - частному, получается, что А - это общее или единичное утверждение, Е - общее или единичное отрицание, I - частное утверждение, а О - частное отрицание.
Теперь дадим примеры категорических суждений, используя стандартную форму записи.
А: Всякий кашалот есть кит (общее утверждение). Марс есть планета (единичное утверждение).
Е: Ни один кот не есть кит (общее отрицание). Марс не есть звезда (единичное отрицание).
I: Некоторые коты суть (есть) черные.
О: Некоторые коты не суть (не есть) черные.
Изучающие логику часто недоумевают по поводу стандартной формы выражения суждений, и иногда доходит до резких выступлений против ее использования в какой бы то ни было практической деятельности. Заявляют, что эта форма - совершенно искусственная, что ее применение - насилие над русским языком, что если кто-то так говорит, то только потому, что к этому принуждают преподаватели логики.
Несмотря на явную неумеренность обвинений, подобные претензии не стоит игнорировать, ибо в них есть рациональное зерно: говорить стандартно всегда и везде - глупо. В повседневном общении мы обычно высказываем суждения короче и изящнее по сравнению с тем, что предлагает логика, но очень часто жертвой этой краткости и изящности становится точность выражения мыслей: фразы получаются расплывчатыми, двусмысленными, а иногда и многозначными. Если дело не требует максимальной точности общения, почему бы и не пренебречь ею? Но в некоторых случаях (например, в научных дискуссиях, при судебном разбирательстве и т.п.) нужно выражать свои мысли предельно четко, недвусмысленно. Вот для таких случаев и разработана стандартная форма выражения суждений.
Стандартная форма выражения суждений нужна для того, чтобы высказывание было точным.
|
|
Ее особенность, которая сразу бросается в глаза, - обязательное использование глагола-связки "быть". Наличие этого глагола значительно упрощает логический анализ суждения, так как, во-первых, легко определить качество последнего (есть отрицательная частица перед связкой - отрицание, нет - утверждение), а во-вторых - легко назвать понятия, играющие роль субъекта и предиката (Например, перейдя от нестандартной формы выражения "Щенку холодно" к стандартной "Щенок есть испытывающий холод", гораздо проще грамотно указать субъект и предикат данного суждения: это - понятия "щенок" и "испытывающий холод" соответственно).
|
Основные особенности стандартной формы выражения суждений: 1) наличие глагола-связки "быть" и 2) использование стандартных кванторных выражений.
|
Вторая особенность стандарта для категорических суждений - строго определенное начало соответствующих им высказываний (исключение - единичные суждения). Об этом говорит сайт https://intellect.icu . Стандартно начинают со следующих кванторных (определяющих количество суждения, т.е. количественно характеризующих субъект) выражений: общее утверждение - с кванторного слова "всякий" (варианты: "каждый", "любой"), общее отрицание - со словосочетания "ни один", частные суждения - со слова "некоторые".
В учебниках общее утверждение, как правило, предлагают высказывать, начиная со слова "все", однако оно логически ущербно в силу своей двусмысленности: в одних случаях "все" означает абстрактный охват элементов данного множества (элементы автономны), в других случаях - конкретный (элементы связаны в целое). Пример: "Все мои товарищи - студенты" и "Все мои товарищи - дружная компания".
Что касается частных суждений, то здесь следует отметить следующее: формальная логика использует кванторное выражение "некоторые" в смысле "хотя бы один, а может, и все", но этот смысл редко встречается в повседневном общении. Гораздо чаще "некоторые" означает "два или больше, но не все".
Как относятся друг к другу категорические суждения разных видов? Прежде чем ответить на этот вопрос, введем ряд определений.
1. Суждение вида А совместимо (не совместимо) с суждением вида В по истине (лжи), если имеется (не имеется) такая пара конкретных суждений этих видов про одно и то же, что оба они истинны (ложны). Здесь в одной фразе даны четыре определения: совместимости по истине, несовместимости по истине, совместимости по лжи и несовместимости по лжи.
2. Из суждения вида А следует суждение вида В, если при истинном суждении первого вида всегда истинно суждение второго вида про то же самое.
3. Отношение подчинения: из суждения вида А следует суждение вида В, но из суждения вида В не следует суждение вида А.
4. Отношение контрарности (противоположности): совместимость по лжи и несовместимость по истине.
5. Отношение субконтрарности: совместимость по истине и несовместимость по лжи.
6. Отношение контрадикторности: несовместимость как по истине, так и по лжи.
|
|
Теперь вернемся к категорическим суждениям. По вертикалям "логического квадрата" (между видами А и I, с одной стороны, и видами Е и О - с другой) имеет место отношение подчинения, по диагоналям (пары А - О и I - Е) - отношение контрадикторности, верхняя сторона квадрата (виды А и Е) - отношение контрарности, нижняя (виды I и О) - отношение субконтрарности.
|
Между категорическими суждениями разного вида существуют разного вида отношения.
|
От простых суждений перейдем к сложным, т.е. к тем, в которых имеются хотя бы две части, в свою очередь представляющие собой суждения. Сложные суждения различают по логическим связям между их частями. При этом выделяют четыре основных вида:
1) Соединительные (конъюнктивные) суждения. Пример: "Идет дождь, и светит солнце". Союза "и" между частями может и не быть, но, если его можно поставить, высказывание выражает соединительное суждение. Пример: "Идет дождь, светит солнце".
2) Разделительные (дизъюнктивные) суждения. Здесь два подвида: а) нестрогие разделительные (Пример: "Петр шашист или шахматист") и б) строго разделительные (Пример: "Или Петр шашист, или шахматист").
3) Условные суждения. Здесь тоже две разновидности: а) импликативные (связь только по истинностным значениям) и б) каузальные (причинно-следственные). Обе разновидности условных суждений обычно высказывают, используя оборот "если …, то", но смысл этого оборота для каждого подвида свой. Возьмем для сравнения две фразы: "Если Москва - столица России, то Париж - столица Франции" и "Если Москва - столица России, то она центр российской политической жизни". Первая фраза выражает импликативное суждение (связь абстрактная, по истинностным значениям), вторая - каузальное (связь конкретной причины с конкретным следствием). Символическая запись: для импликативного суждения - А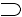 В, для каузального - А
В, для каузального - А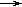 В.
В.
4) Отождествляющие суждения (суждения об эквивалентности). Стандартно их высказывают с оборотом "если и только если …, то". Пример: "Если и только если этот месяц - февраль, то он самый короткий".
|
|

Отношения между суждениями
по "логическому квадрату"
По наличию оценки информации со стороны того, кто судит, суждения делят на два типа: ассерторические (в них такой оценки информации нет) и модальные (такая оценка есть). Из ассерторического суждения всегда можно получить модальное, введя модальное понятие, т.е. понятие какой-то оценки. Например, вместо ассерторического суждения "Земля круглая", можно получить модальные суждения "Хорошо, что Земля круглая", "Необходимо, что Земля круглая" и т.п. По характеру оценки различают виды модальности.
Рассмотрим алетическую модальность. Алетическим называется суждение с модальным понятием "необходимо", "возможно" или "случайно". Алетические суждения с разными модальными понятиями могут быть эквивалентны друг другу. Если необходимость обозначить прямоугольником, возможность ромбом, случайность треугольником, буквой "А" - ассерторическое суждение, а символом "~" - эквивалентность суждений, то схемы эквивалентности алетических суждений будут выглядеть так:
1)  А ~
А ~ 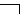
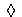 А (Пример: суждению "В наше время необходимо изучать логику" эквивалентно суждение "В наше время невозможно не изучать логику").
А (Пример: суждению "В наше время необходимо изучать логику" эквивалентно суждение "В наше время невозможно не изучать логику").
2) 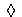 А ~
А ~ 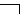
 А (Пример: суждению "Здесь можно ошибиться" эквивалентно суждение "Не является необходимым, чтобы здесь не возникло ошибки").
А (Пример: суждению "Здесь можно ошибиться" эквивалентно суждение "Не является необходимым, чтобы здесь не возникло ошибки").
3)  А ~
А ~ 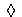 А
А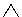
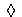
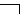 А (Пример: суждению "Ружье выстрелило случайно" эквивалентно суждение "Ружье могло выстрелить, а могло и не выстрелить").
А (Пример: суждению "Ружье выстрелило случайно" эквивалентно суждение "Ружье могло выстрелить, а могло и не выстрелить").
Отрицание суждения - это логическая операция, в ходе которой истинностное значение суждения меняется на противоположное. Обычно отрицают ложь, а истину отрицают лишь по недоразумению, поэтому, приводя пример отрицания суждения, следует исходить из лжи.
При отрицании категорического суждения количество и качество последнего меняют на противоположные. Уточнение: для единичного суждения количество не меняется. Пример: в результате отрицания суждения "Всякий кит есть рыба" получается суждение "Некоторые киты не суть рыбы". У тех, кто помнит, что в формальной логике "некоторые" означает "хотя бы один, а может, и все", сомнений в истинности полученного суждения не возникает. Если же в данном примере мы объявим результатом отрицания суждение "Ни один кит не есть рыба", то произойдет логическая ошибка: мы выполним отрицание неправильно (не по правилу формальной логики).
Схемы отрицания некоторых сложных суждений:
1) Отрицание соединительного суждения. 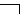 (А
(А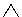 В) ~
В) ~ 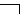 А
А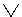
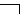 В. Пример: в результате отрицания суждения "Сейчас пасмурно и дождливо" получается "Сейчас не пасмурно или не дождливо".
В. Пример: в результате отрицания суждения "Сейчас пасмурно и дождливо" получается "Сейчас не пасмурно или не дождливо".
2) Отрицание нестрогого разделительного суждения. 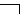 (А
(А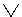 В) ~
В) ~ 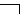 А
А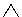
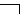 В. Пример: отрицая суждение "Сейчас светит солнце или идет дождь", получаем суждение "Сейчас не светит солнце и не идет дождь".
В. Пример: отрицая суждение "Сейчас светит солнце или идет дождь", получаем суждение "Сейчас не светит солнце и не идет дождь".
3) Отрицание каузального суждения. 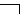 (А
(А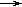 В) ~
В) ~ 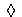 (А
(А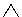
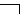 В). Пример: отрицая суждение "Если студент отличник, то он любит логику", получаем суждение "Студент может быть отличником, но при этом не любить логику".
В). Пример: отрицая суждение "Если студент отличник, то он любит логику", получаем суждение "Студент может быть отличником, но при этом не любить логику".
|
|
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про суждение Надеюсь, что теперь ты понял что такое суждение, абстрактная мысль и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика