Лекция
Привет, Вы узнаете о том , что такое отношения между понятиями, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое отношения между понятиями, ограничение понятия, обобщение понятия, объем понятия , настоятельно рекомендую прочитать все из категории Логика.
Содержание понятия — совокупность тех свойств, которые присущи всем предметам, обозначаемым данным понятием, и только им.
К примеру, склероз — это, как известно, уплотнение каких-либо органов, вызванное гибелью специфических для этих органов элементов и заменой их соединительной тканью. Перечисленные свойства составляют содержание понятия «склероз». Они позволяют относительно любой ситуации решить, можно ли назвать происшедшие в органе изменения склерозом или нет. Содержание понятия «стул» составляют свойства быть предметом мебели, предназначенным для сидения, и иметь ножки, сиденье и спинку. Этими свойствами, относящимися к функциям стула и его строению, обладает каждый стул и не обладает ничто иное. Если изъять из числа структурных частей стула, скажем, спинку, получим содержание уже иного понятия («табурет»). В содержание понятия «стол» входят признаки быть предметом мебели, предназначенным для сидения за ним, и иметь ножки и крышку.
Помимо содержания, или смысла, понятие имеет также объем.
объем понятия — совокупность, или класс, тех предметов, которые обладают признаками, входящими в содержание понятия.
Например, в объем понятия «склероз» входят все случаи склеротического изменения органов, в частности склероз мозга. Объем понятия «стул» включает все стулья, объем понятия «стол» — все столы. Нетрудно заметить, что объемы даже таких простых понятий, как «стул» и «стол», являются неопределенными, размытыми, а значит, сами эти имена относятся к неточным.
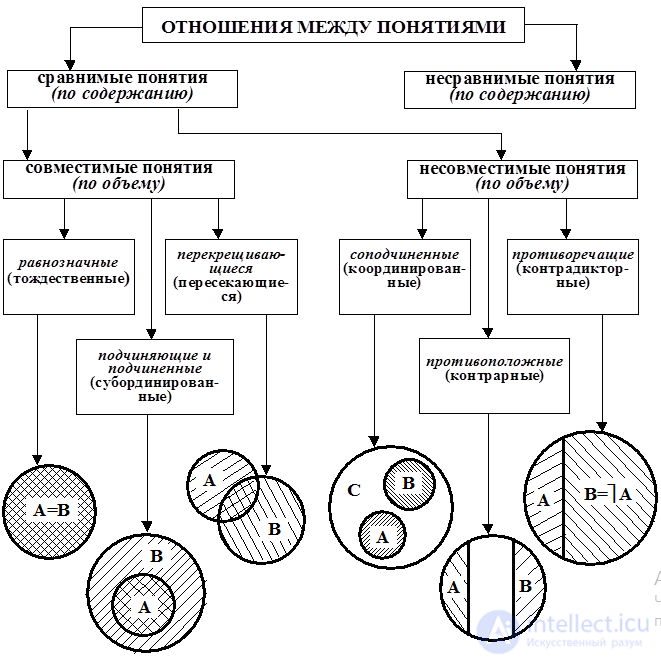
Понятия находятся в различных отношениях друг к другу. Между объемами двух произвольных понятий, которые есть какой-то смысл сопоставлять друг с другом, имеет место одно и только одно из следующих отношений: равнозначность, пересечение, подчинение (два варианта) и исключение.
Равнозначность — отношение между понятиями, объемы которых полностью совпадают.
Иными словами, равнозначные понятия отсылают к одному и тому же классу предметов, но делают это разными способами. Равнозначны, к примеру, понятия «квадрат» и «равносторонний прямоугольник»: каждый квадрат является равносторонним прямоугольником, и наоборот.
Равнозначность означает совпадение объемов двух понятий, но не их содержаний. Например, объемы понятий «сын» и «внук» совпадают (каждый сын есть чей-то внук и каждый внук — чей-то сын), но содержания их различны.
Отношения между объемами понятий можно геометрически наглядно представить с помощью круговых схем. Они называются по имени русского математика XVIII в. Л. Эйлера «кругами Эйлера». Каждая точка круга представляет один предмет, входящий в объем рассматриваемого понятия. Точки вне круга представляют предметы, не подпадающие под это понятие.
Логические операции с понятиями, – и на это обратим особое внимание , – часто дополняются и усиливаются специальным приемом, получившим название метода диаграмм Эйлера-Венна . Эти диаграммы иногда называют "круговыми диаграммами". С помощью такого приема можно наглядно изобразить отношения между объемами сравниваемых понятий. Впервые этот метод систематически стал применять в логике знаменитый математик Л. Эйлер (1707-1783) , но сами круговые изображения объемов понятий уже применялись в VI в. н.э. в афинской неоплатоновской школе математиком Филопоном .
Суть этого метода состоит в том, что изображаемый круг условно включает в себя предметы, отображаемые каким-либо понятием, а каждый из этих предметов обозначается внутри этого круга точкой . Данный круг может включать в себя другой круг, меньшего диаметра, и это означает, что родовое понятие (больший круг) включает в себя видовое понятие (меньший круг).
В дальнейшем английским логиком Джоном Венном (1834-1923) данный метод был распространен на все виды логических отношений, а сами изображения стали фиксироваться не только в виде кругов, но и в виде, скажем, эллипсов.
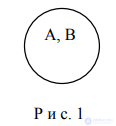
Объемы родового и видового понятий могут как совпадать друг с другом (см. рис. 1), так и не совпадать друг с другом (см. рис. 2). Иллюстрациями здесь соответственно могут служить следующие высказывания: "Каждый человек (A) имеет право на гражданство (B) " (см. рис. 1) и "Все следователи (A) – юристы (B) " (см. рис. 2).
В тех случаях, когда объемы двух понятий совпадают лишь частично, отношение между объемами таких понятий изображается посредством перекрещивающихся кругов (см. рис. 3). Например : "Многие участники Великой Отечественной войны (A) награждены боевыми орденами (B) ". На диаграмме (см. рис. 3) этому высказыванию соответствует заштрихованная часть, являющаяся общей для субъекта и предиката суждения.
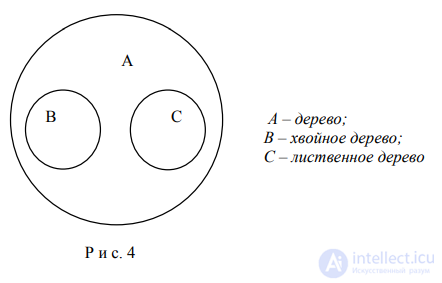
Приведенные случаи являются случаями совместимости понятий по объему. Однако понятия могут быть и несовместимыми по объему. Например , в высказывании – "Несовершеннолетние (A) не имеют права голоса (B) " – A и B несовместимы. На круговой диаграмме это отображается так, как показано на рис.4. Нетрудно видеть, что и A , и B могут входить в общий для них род (C) .
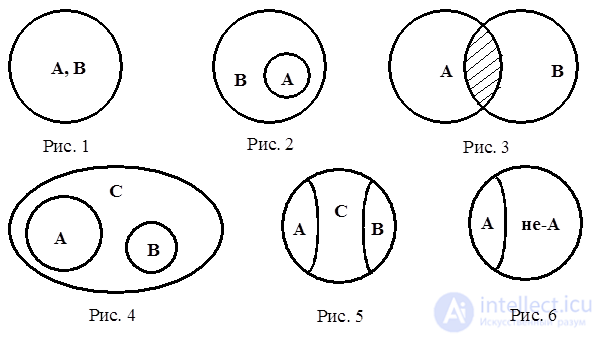
В тех случаях, когда между понятиями имеются отношения противоположности , отношения между объемами таких понятий отображаются посредством одного круга (см. рис. 5). Например : "Все, что имеет начало (A) , имеет и конец (B) " (см. рис. 5). Видно, что в случае наличия противоположных понятий имеется еще и понятие-посредник (C – (A + B )). Если же такой "средней" части не имеется, то данное отношение считается противоречием (см. рис. 6). Например : "Ни один невиновный (A) не должен квалифицироваться как виновный (B) ".
Диаграммы Эйлера-Венна своим наглядным графическим изображением не только облегчают запоминание структуры различных сочетаний мыслей, но и помогают решению ряда логических задач, возникающих в различных областях человеческой деятельности .
Отношения между двумя равнозначными понятиями изображаются в виде двух полностью совпадающих кругов.
.
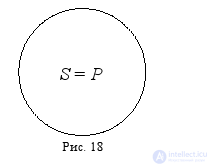
В суждении: «Все квадраты – это равносторонние прямоугольники», – субъект «квадраты» и предикат «равносторонние прямоугольники» находятся в отношении равнозначности, потому что представляют собой равнозначные понятия (квадрат – это обязательно равносторонний прямоугольник, S = P а равносторонний прямоугольник – это обязательно квадрат) (рис. 18).
1. В отношении равнозначности (рис.1) находятся понятия, в которых мыслится один и тот же предмет.
Объемы этих понятий полностью совпадают.
Например:
А – самый большой город Татарстана,
В – столица Татарстана.
2. В отношении пересечения (рис. 2) находятся понятия, имеющие некоторые общие признаки, т,е, объем одного из них частично входит в объем другого:
А – студент; В – спортсмен.
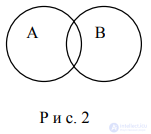
Пересечение — отношение между понятиями, объемы которых частично совпадают.
В суждении:
«Некоторые писатели – это американцы», – субъект «писатели» и предикат «американцы» находятся в отношении пересечения, т. к. являются пересекающимися понятиями (писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть) (рис. 19).
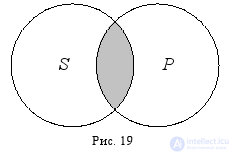
Пересекаются, например, понятия «летчик» и «космонавт»: некоторые летчики являются космонавтами; некоторые летчики — некосмонавты; некоторые космонавты — нелетчики.
Подчинение — отношение между понятиями, объем одного из которых полностью входит в объем другого.
В суждении:
«Все тигры – это хищники», – субъект «тигры» и предикат «хищники» находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия (тигр – это обязательно хищник, но хищник не обязательно тигр). Так же в суждении: «Некоторые хищники являются тиграми», – субъект «хищники» и предикат «тигры» находятся в отношении подчинения, будучи родовым и видовым понятиями. Итак, в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката (рис. 20, a), или наоборот (рис. Об этом говорит сайт https://intellect.icu . 20, б).

3. В отношении подчинения (рис. 3) находятся понятия, одно из которых полностью входит в объем другого:
А – населенный пункт;
В – город.
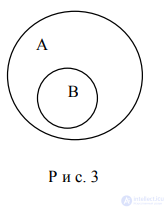
Р и с. 3
Понятие с бóльшим объемом А называется подчиняющим, понятие с меньшим объемом В – подчиненным. Если в отношении подчинения находятся общие понятия, то подчиняющее понятие называется родом, подчиненное – видом. Отношение «род» - «вид» широко используется в логических операциях, выполняемых над понятиями, - обобщение, ограничение, определение, деление.
В отношении подчинения находятся, к примеру, понятия «треугольник» и «прямоугольный треугольник»: каждый прямоугольный треугольник является треугольником, но не каждый треугольник - прямоугольный.
В этом же отношении находятся имена «дедушка» и «внук»: каждый дедушка есть чей-то внук, но не каждый внук является дедушкой. «Внук» — подчиняющее имя, «дедушка» — подчиненное.
Подчиняющее понятие называется родом, а подчиненное — видом. Понятие «треугольник» есть род для вида «прямоугольный треугольник», а понятие «внук» — род для вида «дедушка».
Исключение — отношение между понятиями, объемы которых полностью исключают друг друга.
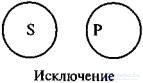
4. Два понятия находятся в отношении соподчинения к третьему (рис. 4), если они не имеют общих элементов объема и это третье понятие является подчиняющим для каждого из них: А – дерево; В – хвойное дерево; С – лиственное дерево
Исключают друг друга понятия «трапеция» и «пятиугольник», «человек» и «планета», «белое» и «красное» и т.п.
Можно выделить два интересных вида исключения:
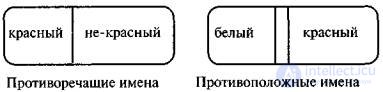
Исключающие объемы дополняют друг друга так, что в сумме дают весь объем рода, видами которого они являются. Понятия, таким образом исключающие друг друга, называютсяпротиворечащими.
Противоречащими являются, например, понятия «умелый» и «неумелый», «стойкий» и «нестойкий», «красивый» и «некрасивый» и т.н. Противоречат друг другу также понятия «простое число» и «число, не являющееся простым», исчерпывающие объем родового понятия «натуральное число», имена «красный» и «не являющийся красным», исчерпывающие объем родового понятия «предмет, имеющий цвет», и т.п.
Исключающие понятия, составляющие в сумме только часть объема того рода, видами которого они являются, называются противоположными.
5. В отношении противоречия (рис. 5) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки отрицает, не заменяя их другими признаками: А – черный; В – не черный
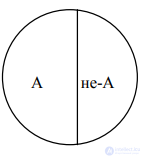
Рис.5
6. В отношениях противоположности (рис. 6) находятся понятия, одно из которых содержит некоторые признаки отрицает, заменяя их исключающими признаками: А – черный; В – белый.
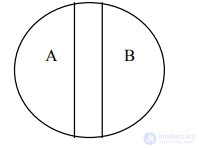
Р и с. 6
К противоположным относятся, в частности, понятия «простое число» и «четное число», не исчерпывающие объема родового понятия «натуральное число», понятия «красный» и «белый», не исчерпывающие объема родового понятия «предмет, имеющий цвет» и т.п.
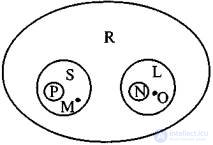
Круговые схемы могут применяться для одновременного представления объемных отношений более чем двух понятий. Такова, к примеру, приводимая на рисунке схема, представляющая отношения между объемами понятий «планета» (Б), «планета Солнечной системы» (Р), «Земля» (Л/), «спутник» (Ь), «искусственный спутник» (М), «Луна» (О) и «небесное тело» (/?). Согласно этой схеме существуют, в частности, небесные тела, не являющиеся ни планетами, ни их спутниками; планеты, не входящие в Солнечную систему; спутники, не являющиеся искусственными, и т.д. Объемы единичных имен представляются точками.
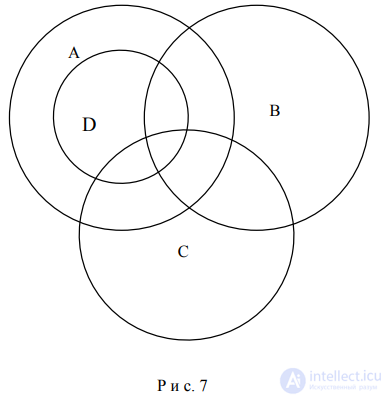
7. При изображении отношений более чем двух понятий сначала определяются отношения каждого с каждым, а затем вычерчивается общая схема, отображающая эти отношения. Например, отношения между объемами понятий А – «студент», В – «волонтер», С – А В А не-А 7 «спортсмен», D – «студент ЕГПУ» можно изобразить схемой, представленной на рис. 7:
Как правило, все суждения подразделяют на три вида:
1. Атрибутивные суждения (от лат. attributum – атрибут) – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение: «Все воробьи – это птицы», – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта: быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей). Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении: «Некоторые птицы – это воробьи» (как видим, по сравнению с вышеприведенным примером, субъект и предикат поменялись местами), субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.
2. Экзистенциальные суждения (от лат. existentia – существование) – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение: «Вечных двигателей не бывает», – является экзистенциальным, т. к. его предикат «не бывает» свидетельствует о несуществовании субъекта (вернее –предмета, который обозначен субъектом).
3. Релятивные суждения (от лат. relativus – относительный) – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение: «Москва основана раньше Санкт-Петербурга»,– является релятивным, потому что его предикат «основана раньше Санкт-Петербурга» указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.
Итак, в логике выделяется шесть вариантов отношений между понятиями. Для удобства их запоминания они представлены в табл. 2.
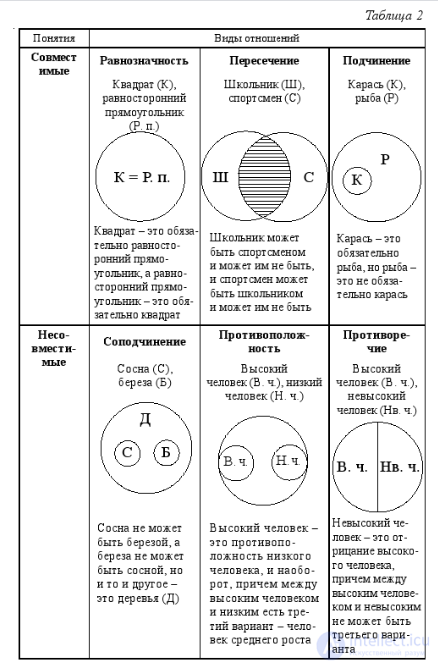
Любые два сравнимых понятия обязательно находятся в одном из шести указанных случаев отношений. Например, понятия «писатель» и «россиянин» находятся в отношении пересечения, «писатель» и «человек» – подчинения, «Москва» и «столица России» – равнозначности, «Москва» и «Санкт-Петербург» – соподчинения, «мокрая дорога» и «сухая дорога» – противоположности, «Антарктида» и «материк» – подчинения, «Антарктида» и «Африка» – соподчинения и т. д. Надо обратить внимание на то, что если два понятия обозначают часть и целое, например «месяц» и «год», то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год.
Однако если бы понятия «месяц» и «год» были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий «карась» и «рыба»: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия «месяц» и «год», так же, как и понятия «книга» и «страница книги», «автомобиль» и «колесо автомобиля», «молекула» и «атом», находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, но это можно сделать и с большим числом понятий.
Например, отношения между понятиями «боксер» (Б), «норвежец» (Н) и «человек» (Ч) изображаются следующей схемой Эйлера (рис. 7).
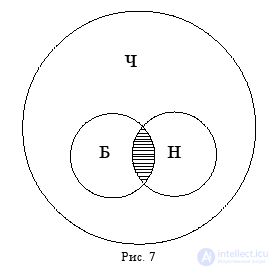
Взаимное расположение кругов показывает, что понятия «боксер» и «норвежец» находятся в отношении пересечения: боксер может быть норвежцем и может им не быть, а норвежец также может быть боксером и может им не быть, а понятия «боксер» и «человек», так же как понятия «норвежец» и «человек», находятся в отношении подчинения: любой боксер и любой норвежец– это обязательно человек, но человек может не быть ни боксером, ни норвежцем.
Рассмотрим отношения между понятиями «дедушка» (Д), «отец» (О), «мужчина» (М), «человек» (Ч) с помощью схемы Эйлера (рис. 8).
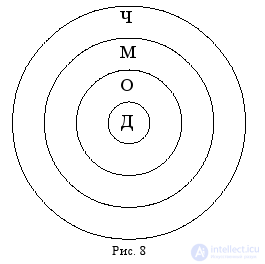
Указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина.
Отношения между понятиями «хищник» (Х), «рыба» (Р), «акула» (А), «пиранья» (П), «щука» (Щ), «живое существо» изображаются следующей схемой Эйлера (рис. 9).
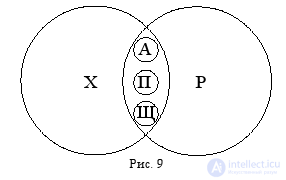
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая все сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того чтобы можно было установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными.
Видовые и родовые понятия тесно связаны между собой логическими операциями ограничения и обобщения.
ограничение понятия – это логическая операция перехода от родового понятия к видовому с помощью прибавления к его содержанию какого-либо признака (или нескольких признаков).
Вспомним об обратном отношении между объемом и содержанием понятия: чем больше объем, тем меньше содержание, и наоборот. Ограничение понятия, или переход от родового понятия к видовому – это уменьшение его объема, а значит – увеличение содержания. Вот почему при добавлении каких-либо признаков к содержанию понятия автоматически уменьшается его объем. Например, если к содержанию понятия «физический прибор» (Ф. п.) прибавить признак «измерять напряжение электрического тока», то оно превратится в понятие «вольтметр» (В), которое будет видовым по отношению к исходному родовому понятию «физический прибор» (рис. 10).
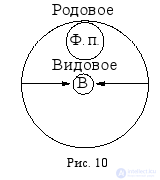
Так же, если к содержанию понятия «геометрическая фигура» (Г. ф.) прибавить признак «иметь равные стороны и прямые углы», то оно превратится в понятие «квадрат» (К), которое будет видовым по отношению к исходному родовому понятию «геометрическая фигура» (рис. 11).

Обобщение понятия – это логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания какого-либо признака (или нескольких признаков). Содержание понятия, лишенное каких-то признаков, уменьшается, но при этом автоматически увеличивается объем понятия, которое из видового становится родовым или обобщается. Например, если от содержания понятия «биология» (Б) отбросить признак «изучать различные формы жизни», то оно превратится в понятие «наука» (Н), которое будет родовым по отношению к исходному видовому понятию «биология» (рис. 12).
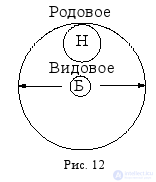
Так же, если от содержания понятия «атом водорода» (А. в.) отбросить признак «иметь один электрон», то оно превратится в понятие «атом химического элемента» (А. х. э.), которое будет родовым по отношению к исходному видовому понятию «атом водорода» (рис. 13).
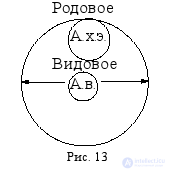
Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие «Солнце», то получится следующая цепочка: Солнце → звезда →небесное тело→ → физическое тело → форма материи. В этой цепочке понятие «звезда» является родовым по отношению к понятию «Солнце», но видовым по отношению к понятию «небесное тело»; так же понятие «небесное тело» является родовым по отношению к понятию «звезда», но видовым по отношению к понятию «физическое тело» и т. д. Движение по нашей цепочке от понятия «Солнце» к понятию «форма материи» представляет собой серию последовательных обобщений, а движение в обратном направлении – серию ограничений. Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький будет обозначать понятие «Солнце», а самый большой – «форма материи».
Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие (см. раздел 1.1.), а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие, например: объект мироздания, форма материи или форма бытия.
Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некого целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия «цветок» предлагают понятие «стебель». Действительно, стебель – это часть цветка, но ограничить понятие – значит подобрать не часть для целого, а вид для рода. Следовательно, правильным ограничением понятия «цветок» будет понятие «ромашка», или «тюльпан», или «хризантема» и т. п. В качестве обобщения понятия «дерево» нередко предлагают понятие «лес». Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – значит подобрать не целое для части, а род для вида. Следовательно, правильным обобщением понятия «дерево» будет понятие «растение», или «объект флоры», или «живой организм» и т. п.
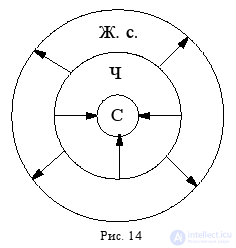
Итак, почти любое понятие (за исключением единичных и широких, философских) можно как ограничить, так и обобщить. Другими словами, подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия «человек» (Ч) будет понятие «спортсмен» (С) или «писатель», или «мужчина», или «молодой человек» и т. п., а его обобщением будет понятие «живое существо» (Ж. с.) (рис. 14).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
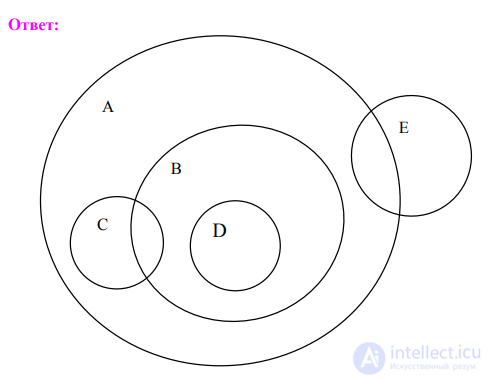
П р и м е р 1. Представьте с помощью круговой схемы Эйлера отношения между следующими понятиями:
Игрушка ( А), заводная игрушка ( В), кукла ( С), заводной автомобиль (D), пистолет (E)
2. Представьте с помощью круговой схемы отношения между следующими понятиями: Молния (А), поджог ( В), причина пожара (С), пожар (D), взрыв
атомной бомбы (Е).
П р и м е р 3. Представьте с помощью круговой схемы отношения между следующими понятиями: Планета (A), планета Солнечной системы (B), Земля (C), спутник ( D), искусственный спутник (E), Луна (F), небесное тело (G).
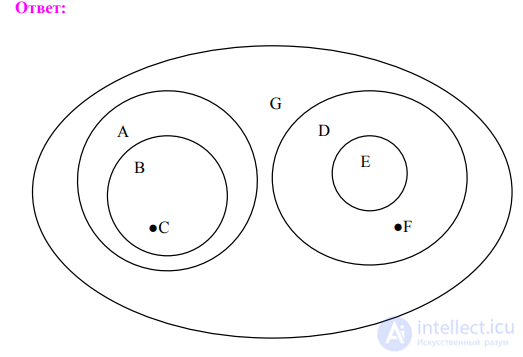
П р и м е р 4. Найдите понятия, отношения между которыми удовлетворяли бы приведенной круговой схеме:
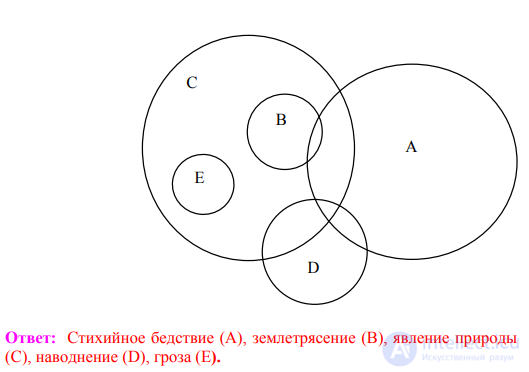
Ответ: Стихийное бедствие (А), землетрясение (В), явление природы (С), наводнение (D), гроза (Е).
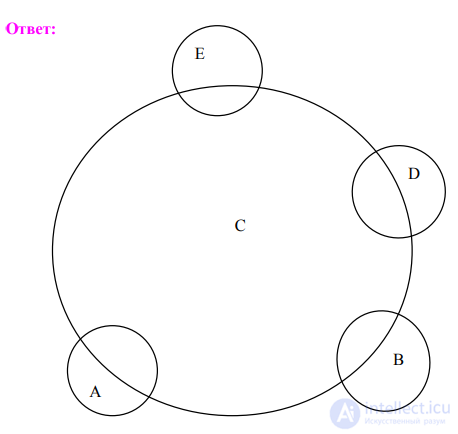
П р и м е р 5. Найдите понятия, отношения между которыми удовлетворяли бы приведенной круговой схеме:
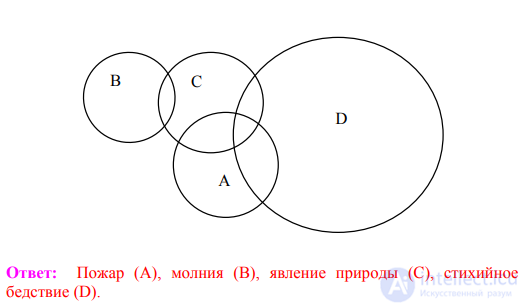
Ответ: Пожар (А), молния (В), явление природы (С), стихийное бедствие (D).
1. Что такое ограничение понятия?
2. Что представляет собой логическая операция обобщения понятия?
3. Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?
4. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом.
5. Всякое ли понятие можно подвергнуть ограничению или обобщению? Какие понятия не поддаются этим логическим операциям?
6. Подберите десять любых понятий и проделайте с ними ограничение и обобщение, т. е. подберите для каждого как видовое, так и родовое понятие, иллюстрируя эти операции схемами Эйлера.
7. Суждение: «Бога нет», – является:
8. Атрибутивным является суждение:
9. Субъект и предикат находятся в отношении пересечения в суждении:
10. Релятивным является суждение: выберите один или несколько ответов:
11 Термин простого атрибутивного суждения является нераспределенным, если в этом суждении:
12 Суждения: «Все хищники – животные», «Тигры – это животные», – находятся в отношении:
14. Отношения между понятиями изображаются:
15 Деление понятия раскрывает его:
Прочтение данной статьи про отношения между понятиями позволяет сделать вывод о значимости данной информации для обеспечения качества и оптимальности процессов. Надеюсь, что теперь ты понял что такое отношения между понятиями, ограничение понятия, обобщение понятия, объем понятия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Комментарии
Оставить комментарий
Логика
Термины: Логика