Лекция
Привет, Вы узнаете о том , что такое условно-категорический силлогизм, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое условно-категорический силлогизм, эквивалентно-категорический силлогизм, чисто условный силлогизм, условный силлогизм , настоятельно рекомендую прочитать все из категории Логика.
силлогизм - Логическое умозаключение, в к-ром из двух данных суждений (посылок) получается третье (вывод).
условно-категорический силлогизм – силлогизм, в котором большая посылка является условным, а меньшая – категорическим суждением.
чисто условный силлогизм – силлогизм, в котором обе посылки и вывод являются условными суждениями
эквивалентно-категорический силлогизм – силлогизм, в котором бóльшая посылка является выделяющим условным, а меньшая – категорическим суждением.
Умозаключения, которые содержат в себе условные (импликативные) суждения называются условными. В мышлении и речи часто используется условно-категорический силлогизм, название которого свидетельствует о том, что в нем первая посылка является условным (импликативным) суждением, а вторая посылка – простым (категорическим). Например:
Если взлетная полоса покрыта льдом, то самолеты не могут взлетать.
Сегодня взлетная полоса покрыта льдом.
Сегодня самолеты не могут взлетать.
Условно-категорический силлогизм имеет два модуса:
1. Утверждающий модус, у которого первая посылка представляет собой импликацию, состоящую, как мы уже знаем, из двух частей – основания и следствия, вторая посылка является утверждением основания, а в выводе утверждается следствие. Например:
Если вещество – металл, то оно электропроводно.
Данное вещество – это металл.
Данное вещество электропроводно.
Форма утверждающего модуса условно-категорического силлогизма: ((a → b) ∧ a) → b, где (a → b) – это первая посылка в виде импликации основания и следствия; ((a → b) ∧ a) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и утверждения основания; b – это вытекающий из посылок вывод силлогизма в виде утверждения следствия.
2. Отрицающий модус, у которого первая посылка представляет собой импликацию основания и следствия, вторая посылка является отрицанием следствия, а в выводе отрицается основание.
Например:
Если вещество – металл, то оно электропроводно.
Данное вещество неэлектропроводно.
Данное вещество – не металл.
Форма отрицающего модуса условно-категорического силлогизма: ((a → b) ∧¬ b) → ¬ a, где (a → b) – это первая посылка в виде импликации основания и следствия; ((a → b) ∧ ¬b) – это две посылки силлогизма в виде двухчленной конъюнкции, состоящей из уже упомянутой импликации и отрицания следствия; ¬ a – это вытекающий из посылок вывод силлогизма в виде отрицания основания.
Необходимо обратить внимание на уже известную нам особенность импликативного суждения, которая состоит в том, что основание и следствие нельзя поменять местами. Например, высказывание: «Если вещество – металл, то оно электропроводно», – является верным, т. к. все металлы – это электропроводники (из того, что вещество – металл, с необходимостью вытекает его электропроводность). Однако высказывание: «Если вещество электропроводно, то оно – металл», – неверно, т. к. не все электропроводники являются металлами (из того, что вещество электропроводно, не вытекает то, что оно – металл). Эта особенность импликации обусловливает два правила условно-категорического силлогизма:
1. Утверждать можно только от основания к следствию, т. е. во второй посылке утверждающего модуса должно утверждаться основание импликации (первой посылки), а в выводе – ее следствие.
В противном случае из двух истинных посылок может вытекать ложный вывод. Например:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
Слово «Москва» надо писать с большой буквы.
Слово «Москва» всегда стоит в начале предложения.
В силлогизме во второй посылке утверждалось следствие, а в выводе – основание: ((a → b) ∧ b) → a. Это утверждение от следствия к основанию и является причиной ложного вывода при истинных посылках.
2. Отрицать можно только от следствия к основанию, т. е. во второй посылке отрицающего модуса должно отрицаться следствие импликации (первой посылки), а в выводе – ее основание. В противном случае из двух истинных посылок может вытекать ложный вывод. Например:
Если слово стоит в начале предложения, то его надо писать с большой буквы.
В данном предложении слово «Москва» не стоит в начале.
В данном предложении слово «Москва» не надо писать с большой буквы.
В силлогизме во второй посылке отрицается основание, а в выводе – следствие: ((a → b) ∧ ¬ a) → ¬ b. Это отрицание от основания к следствию и является причиной ложного вывода при истинных посылках.
Вспомним, что среди сложных суждений помимо импликации: a → b, есть также эквиваленция: a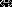
b. Если в импликации всегда выделяется основание и следствие, то в эквиваленции нет ни того, ни другого, т. к. она представляет собой сложное суждение, обе части которого тождественны (эквивалентны) друг другу. Если первой посылкой силлогизма является не импликация, а эквиваленция, то такой силлогизм называется эквивалентно-категорическим. Например:
Если число четное, то оно делится без остатка на 2.
Число 16 – четное.
Число 16 делится без остатка на 2.
Форма модуса данного силлогизма: (a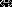b) ∧ a) → b.
Поскольку в первой посылке эквивалентно-категорического силлогизма нельзя выделить ни основания, ни следствия, то рассмотренные выше правила условно-категорического силлогизма к нему неприменимы (в эквивалентно-категорическом силлогизме и утверждать, и отрицать можно как угодно). Если в условно-категорическом силлогизме два модуса правильных и два неправильных (см. выше), то в эквивалентно-категорическом силлогизме все четыре модуса являются правильными:
((a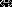b) ∧ a) → b;
((a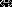b) ∧ b) → a;
((a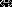b) ∧ ¬ a) → ¬ b;
((a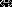b) ∧ ¬ b) → ¬ a.
Читатель без труда сможет подобрать примеры для каждого из четырех модусов эквивалентно-категорического силлогизма.
Если же обе посылки и вывод представляют собой условные суждения, то это чисто условный силлогизм (чисто условное умозаключение). Например:
Если вещество является металлом, то оно электропроводно.
Если вещество электропроводно, то его невозможно использовать в качестве изолятора.
Если вещество является металлом, то его невозможно использовать в качестве изолятора.
Форма модуса данного силлогизма: ((a → b) ∧ (b → c)) → (a → c).
Рис Закон контрапозиции
рис. Об этом говорит сайт https://intellect.icu . Эквивалентно-категорический силлогизм
1. Что представляют собой условные умозаключения?
2. Какие модусы имеет условно-категорический силлогизм? Приведите по три примера для каждого модуса, изобразив их форму с помощью условных логических обозначений.
3. Что называется в условно-категорическом силлогизме «основанием», а что – «следствием»? Каковы правила условно-категорического силлогизма и ошибки, возникающие при их нарушении?
Придумайте по два примера для каждой ошибки, возникающей при нарушении соответствующего правила.
4. Что такое эквивалентно-категорический силлогизм? Чем он отличается от условно-категорического? Почему в условно-категорическом силлогизме только два модуса являются правильными, а в эквивалентно-категорическом – четыре. Придумайте по одному примеру для каждого модуса эквивалентно-категорического силлогизма.
5. Чем отличается чисто условный силлогизм от условно-категорического силлогизма? Приведите два примера чисто условного силлогизма.
6. Допущены ли ошибки (и какие) в следующих условно-категорических силлогизмах:
1) Если животное является млекопитающим, то оно позвоночное.
Рептилии не являются млекопитающими.
Рептилии не являются позвоночными.
2) Если человек льстит, то он лжет.
Этот человек льстит.
Этот человек лжет.
3) Если геометрическая фигура является квадратом, то у нее все стороны равны.
Равносторонний треугольник не является квадратом.
У равностороннего треугольника стороны не равны.
4) Если металл – свинец, то он тяжелее воды.
Данный металл тяжелее воды.
Данный металл – свинец.
5) Если небесное тело является планетой Солнечной системы, то оно движется вокруг Солнца.
Комета Галлея движется вокруг Солнца.
Комета Галлея является планетой Солнечной системы.
Исследование, описанное в статье про условно-категорический силлогизм, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое условно-категорический силлогизм, эквивалентно-категорический силлогизм, чисто условный силлогизм, условный силлогизм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Логика
Из статьи мы узнали кратко, но содержательно про условно-категорический силлогизм
Комментарии
Оставить комментарий
Логика
Термины: Логика