Привет, Вы узнаете о том , что такое дефиниция, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
дефиниция, инфиниция , настоятельно рекомендую прочитать все из категории Логика.
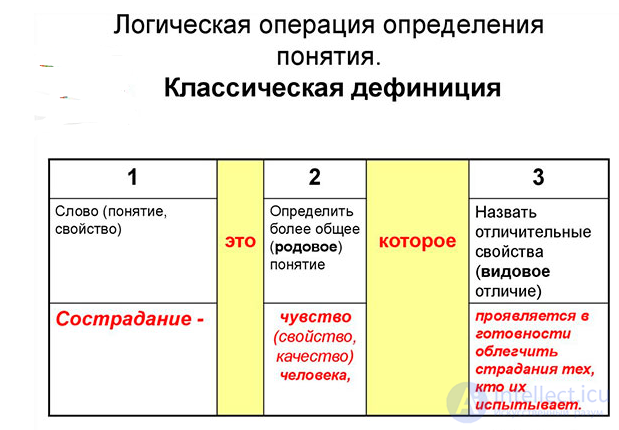
дефиниция , или определение — это логическая операция: 1) раскрывающая содержание (смысл) имени посредством описания существенных и отличительных признаков предметов или явлений, обозначаемых данным именем (денотата имени); 2) эксплицирующая значение термина языка, или понятия.
Дефиниция (образовано от латинского слова: definitio — предел, граница).
Определить термин — значит установить границы его применения. Строгая его дефиниция состоит из двух частей: дефиниендума (dfd) — определяемого имени, и дефиниенса (dfn) — определяющего выражения, раскрывающего смысл определяемого имени либо устанавливающего значение термина. Дефиниендум и дефиниенс должны находиться в отношении тождества, то есть иметь один и тот же денотат, и быть взаимозаменяемыми.
Дефиниции делят по разным основаниям, в частности по способу раскрытия содержания — на явные (указываются признаки, присущие предмету или явлению) и неявные (выявляются отношения, в которых находится определяемый предмет, явление с другими предметами, явлениями).
инфиниция — это понятие постфилософского дискурса, обозначающее отсроченную дефиницию, которая определяет некоторое понятие и вместе с тем демонстрирует его неопределимость.

Инфинициями изобилуют писания Лао-цзы, Чжуан-цзы и других даосистских мыслителей; сочинения по апофатической теологии, в частности, трактаты Псевдо-Дионисия Ареопагита; работы Жака Деррида и других последователей деконструкции. Инфинировать (to infine) — «беспределять», снимать предел, откладывать определение, простирать его в бесконечность. Например, обычно инфинируются (а не дефинируются) такие понятия как «дао», «диферанс», «деконструкция»…
Примеры указанных инфиниций:
«Дао производит полноту и пустоту, но не есть ни полнота, ни пустота; оно производит увядание и упадок, но не есть ни увядание, ни упадок. Оно производит корни и ветви, но не есть ни корень, ни ветвь»
[…] Не-Начало сказало: Дао нельзя услышать: то, что можно услышать, не Оно. Дао нельзя увидеть: то, что можно увидеть, не Оно. Дао нельзя выразить в словах: то, что можно выразить в словах, не Оно. Знаем ли мы Бесформенное, которое дает форму форме? Таким же образом Дао не допускает быть названным».
Чжуан-цзы.
Явные дефиниции могут быть представлены в виде равенства, в котором определяемая часть эквивалентна по объему определяющей части. Они задаются лингвистической конструкцией вида: A ↔ B. Каждая такая конструкция содержит четыре части: A называется определяемой частью, B — определяющей частью, знак «↔» указывает, что выражение A означает то же самое, что и выражение B. В случаях конкретных явных определений вместо знака «↔» пишется либо знак «Df» (читается: «равно по дефиниции»), либо знак «≡ Df» (читается: «эквивалентно по дефиниции»). Первый знак употребляется в том случае, когда определяемая часть A является именной конструкцией, а второй в том случае, когда A — высказывательная конструкция. В определяемой части A, которое может быть сложным выражением, всегда присутствует некоторый термин, который и является целью определения. Этот термин называется определяемым термином. В явных определениях определяемым термином является та минимальная часть определяемого выражения A, которая не встречается в определяющей части.
Явные дефиниции делятся по разным основаниям на несколько видов. В зависимости от того, к какой языковой категории относится определяемый термин, различают их следующие виды:
Атрибутивно-реляционные дефиниции, в которых указывается ближайшее родовое отличие и видовой признак, присущий только данному виду (например, «квадрат — это ромб с прямыми углами»).
Генетические дефиниции, в которых указывается происхождение или способ конструирования объекта, обозначаемого определяемым именем (например, «сфера — пространственная поверхность, которую описывает полуокружность при вращении ее вокруг диаметра»).
Целевые дефиниции, в которых указывается на то, как используется определяемый объект, какие функции он выполняет, для достижения каких целей он применяется.
Квалифицирующие дефиниции, в которых фиксируются, что определяемый объект представляет собой, то есть фиксируются какие-то его структурные особенности, атрибуты, а также особенности внешнего вида.
Перечислительные дефиниции, в которых просто перечисляются те объекты, которые подпадают под определяемый термин.
Операциональные дефиниции, в которых, в качестве видовой характеристики объектов выступает указание на некоторую операцию, посредством которой эти объекты могут быть обнаружены и обозначено их отличие от других предметов (например, «кислота — вещество, окрашивающее лакмус в красный цвет»).
Явные дефиниции обладают одним важным свойством — определяемые и определяющие части могут в любом контексте замещаться друг на друга, то есть для них верно правило замены по дефиниции.
Неявные дефиниции не имеют четко выраженной структуры, вследствие чего отсутствует способ элиминации дефиниендума из того или иного контекста (например, матричное определение логических операций в исчислении высказываний и другие). Они задаются лингвистической конструкцией вида: A есть то, что удовлетворяет условиям: B1, В2, … Βn.
Правила дефиниции
- Правило недопустимости круга — определяющее не должно содержать в себе определяемое. Иными словами: запрещено объяснять значение термина через него самого.
Логика — это наука о логическом мышлении. Физические законы — это законы, которые существуют в физике.
Такие определения не проясняют ситуацию. Мы как не понимали исходный термин, так и не понимаем.
- Правило соразмерности — определяемое должно быть равно определяющему. Термин не должен трактоваться слишком узко или широко.
Пример широкого определения: «Компот — это жидкость».
Существуют тысячи видов жидкостей, и эта дефиниция не позволяет понять, чем компот отличается от них.
Или вот слишком узко: «Художник — это человек, который рисует натюрморты».
Но ведь художник может создавать портреты или пейзажи.
- Ясность — значение должно раскрываться при помощи слов и выражений, понятных для окружающих. Об этом говорит сайт https://intellect.icu . Каждая дефиниция рассчитана на свою аудиторию. Вот мы объясняем маленькому ребенку, что такое черная дыра. Это определение будет отличаться от того, которое бы мы зачитали в рамках доклада на конференции астрофизиков.
Бывает, читаешь и ничего не понятно: «Сингулярность — это точка в пространстве-времени, через которую нельзя гладко продолжить входящую в нее геодезическую линию».
Что еще за геодезическая линия, как ее «гладко продолжить»? Если сложный термин раскрывается при помощи еще более заумных выражений, принцип ясности нарушен.
- Недопустимость метафор и фразеологизмов. Определение должно четко формулировать, чем является объект, без шуток, прибауток и абстрактных рассуждений.
Высказывания «лев — это царь зверей», «хлеб — это всему голова» не соответствуют правилам.
- Определение не должно быть негативным. Отрицание характеристик объекта не дает сформировать о нем полноценное представление.
Вода не считается твердым веществом, а теорема — это не гипотеза.
Здесь понятно, чем не является объект, но все равно неясно, что он собой представляет.
Виды дефиниций
- Интенсиональные. Они выделяют нужный объект из некоего набора. Такая дефиниция может содержать отличительные черты предмета, правила выделения из множества, ссылку на близкие по смыслу предметы.
- Экстенсиональные. Представляют собой перечисление всех объектов, которые попадают под рассматриваемое понятие.
Например, выражение «мировые религии» определяется перечнем крупных религиозных учений.
Эти дефиниции используются, если множество объектов конечно и не слишком велико. Попробуйте пояснить, что такое «животное», перечислением всех видов животных — уйдут недели.
- Генетические. Объект описывается путем указания на способ его создания: «Вода — вещество, которое образуется в результате горения водорода в кислороде».
- Аксиоматические. Объясняют значение слова через набор аксиом (что это?), в которые он входит. В евклидовой геометрии понятия «точка», «прямые», «параллельность» раскрываются через систему постулатов.
- Предписывающие. Они устанавливают, как правильно использовать и трактовать определенные термины.
Вот Уголовный кодекс РФ говорит, что под мошенничеством нужно понимать причинение имущественного ущерба путем обмана или злоупотребления доверием.
Это требование, которому следует вся судебная и правоохранительная система.
- Предметные и семантические. Предметные дефиниции описывают сами объекты и их признаки.
Прямоугольник — это четырехугольник, у которого все стороны равны.
Семантические определения объясняют значения словесных выражений как совокупности знаков.
Под термином «прямоугольник» будем понимать четырехугольник с равными сторонами.
К числу неявных дефиниций относятся:
Аксиоматические дефиниции. Посредством аксиоматических дефиниций некоторый термин определяется путем указания той совокупности аксиом, в которой он содержится. С этой точки зрения аксиомы любой системы являются синтетическими определениями тех терминов, которые в них входят. Так, в научном поиске с помощью аксиоматических определений смысл исходных (примитивных) терминов научной теории задается посредством введения системы постулатов, содержащих данные термины и формулирующих те условия, которым обязаны удовлетворять обозначаемые терминами объекты. В математической логике примером аксиоматической дефиниции может служить определение формулы в исчислении высказываний.
Индуктивные дефиниции. Примером индуктивной дефиниции является определение натурального числа в математике:
- 0 есть натуральное число;
- если n- натуральное число, то nʹ — натуральное число;
- ничто иное не есть натуральное число.
Суть таких дефиниций состоит в следующем. Если требуется задать класс предметов, подпадающих под некоторый термин, то мы прямо объявляем некоторые предметы элементами этого класса. Данный пункт определения называется базисом индукции. После этого все остальные предметы, входящие в класс, порождаются с помощью некоторых процедур. Такой пункт определения называется индуктивным шагом. Третий пункт определения ограничивает класс натуральных чисел только теми объектами, которые задаются первыми двумя пунктами. В общем случае в пункте, задающем базис индукции, может указываться не один предмет, а много предметов, и даже бесконечное их число. С другой стороны, в пунктах, задающих индуктивные шаги, может использоваться не одна порождающая операция, как это имеет место в приведенном примере, а несколько операций. Именно такая ситуация имеет место в индуктивном определении формул логики высказываний. Здесь в базисе индукции любая пропозициональная переменная, а их число бесконечно, объявляется формулой. Порождающими же процедурами в этом случае являются процедуры применения логических констант ¬, &, ∨, ⊃ к ранее построенным формулам.
Рекурсивные дефиниции. Они похожи на индуктивные, но применяются для задания не классов предметов, а некоторых функций. Примером рекурсивной дефиниции может служить определение математического ряда чисел Фибоначчи посредством рекурсивной (возвратной) функции, в котором каждое последующее число равно сумме двух предыдущих чисел: 1, 1, 2, 3, 5, 8 и так далее. Другим примером является следующее определение сложения: 1) x + 0 = х; 2) x + yʹ = (x + y)ʹ. Суть этого определения такова. Понимание некоторой функции состоит в знании ее значений для определенных значений аргументов. Именно это и позволяет установить рекурсивное определение сложения. Действительно, первый пункт, который называется базисом рекурсии, говорит, что значение функции x + y равно x, если y = 0. Второй пункт, который называется рекурсией, говорит, что если мы хотим вычислить значение x + yʹ, где yʹ — число, следующее за y, то надо вычислить для этого y, чему равно x + y, и взять число, следующее за x + y.
Контекстуальные дефиниции, позволяющие, например, возможность выяснить содержание понятия, не прибегая к толковому словарю, а через предлагаемый контекст). В этом случае говорят о некоторой контекстной зависимости определяемого термина. Определяемый термин помещается в некоторый языковой контекст, а ему приравнивается по смыслу другой контекст, не содержащий данного термина. При этом сам термин «контекстная зависимость» понимается в двух различных смыслах. С одной стороны, речь идет о получении некоторого неявного знания об интересующем нас термине из рассмотрения некоторого конкретного контекста, в состав которого он входит. В этом случае понимание смысла контекста позволяет предположить и возможное значение соответствующего термина. С другой стороны, речь вдет об определении термина посредством определения всех контекстов, в состав которых он входит. Чтобы задать эти контексты, используют соответствующий метаязык. В первом случае говорят об определении через контекст; во втором — о контекстуальном определении.
Для всех неявных дефиниций имеют место следующие особенности:
Условия B1, В2, … Βn представляют собой предложения.
Определяемый термин — это то минимальное выражение, которое входит в каждое определяющее условие B1, В2, … Βn, что не влечет тем не менее тавтологичности дефиниций, так как в дефинициях этого сорта определяющая часть (условия B1, В2, … Βn) не приравнивается выражению A.
В силу сказанного для неявных дефиниций не действует правило замены по дефиниции.
В зависимости от выполняемой функции дефиниции делятся на:
1. Реальные дефиниции, определяющие предметы и явления. Определение считается реальным, если значением определяемого термина являются реально (материально) существующие предметы или их характеристики (свойства и отношения). Реальное определение решает задачу образования понятия о предметах, входящих в объем определяемого термина, то есть задачу выделения общего и отличительного признаков этих предметов.
2. Номинальные дефиниции, вводящие новые языковые формы — термины. Определение считается номинальным (образовано от латинского слова: nomen — название, имя), если значением определяемого термина являются предметы реально (материально) не существующие, а также их характеристики. Оно используется в ситуациях, когда термин вводится в языковой контекст как сокращенное название для объектов определенного типа или же когда существует несколько смысловых трактовок определяемого термина и необходимо договорится, какая из них принимается в данном контексте.
В зависимости от цели выполняемой процедуры дефиниции делятся на:
1 Регистрирующие дефиниции, фиксирующие (констатирующие) известное значение некоторого термина без изменений.
2 Уточняющие дефиниции, корректирующие (регулирующие) смысл термина путем предписания значения.
3 Постулирующие дефиниции, посредством которой вводятся новые научные термины или обозначаются вновь открытые явления, созданные предметы и так далее.
Почти все дефиниции относятся к числу родо-видовых, то есть к определениям через указание на род и видовое отличие, так как при формальной записи определений почти любая дефиниция содержит некоторые переменные, пробегающие по какому-то универсуму. Последний как раз и является тем родом, внутри которого с помощью видового отличия выделяются определяемые объекты. Однако среди определений имеются и такие, которые нельзя отнести к родо-видовым. Это так называемые фундаментальные индуктивные определения. Дело заключается в том, что характеристика некоторого определения как родо-видового предполагает, что род уже имеется и потому остается только с помощью видового отличия в этом роде выделить класс определяемых предметов. Однако фундаментальные индуктивные определения не предполагают никакого заранее данного универсума, напротив, они сами строят универсум рассуждения. Примером фундаментального определения может служить рассмотренное выше определение натурального числа.
К дефинициям предъявляются различного рода требования, соблюдение которых гарантирует корректность этой логической операции. Дефиниция как логическая операция должна соответствовать четырем основным правилам:
1 Правило соразмерности и согласованности. В корректной дефиниции объемы определяемого и определяющего имен должны совпадать, то есть должно выполняться равенство: dfd ↔ dfn. При нарушении данного правила возможны три разновидности ошибок: а) ошибка «слишком широкой дефиниции» в случае, когда объем определяемого имени меньше объема определяющего имени: dfd ← dfn; б) ошибка «слишком узкой дефиниции» в случае, когда объем определяемого имени больше объема определяющего имени: dfd → dfn; в) ошибка «слишком широкой и слишком узкой дефиниции» в случае, когда объем определяемого имени оказывается одновременно меньше и больше объема определяющего имени. Так, для всех явных дефиниций при их формальной записи на языке, например, исчисления предикатов, должны выполняться также следующие требования согласованности:
- свободные переменные, входящие в A и B, должны быть одинаковыми;
- должны совпадать типы этих переменных (например, одинаковые предикатные переменные должны быть и одинаковой местности);
- тип выражения A должен совпадать с типом выражения B, то есть если A — имя, то и B должно быть именем, если A — высказывательная форма, то и B должно быть высказывательной формой, и так далее.
2 Правило запрета круга. Дефиниция не должна содержать в себе круга. При нарушении данного правила возможны две разновидности ошибки «круг в дефиниции»: а) «порочный круг» (опосредованный круг), когда определяемое имя определяется через определяющее, а определяющее имя может определяться только через определяемое; б) тавтология (непосредственный круг), когда определяемое и определяющее имена выражены одинаковыми терминами.
3 Правило неотрицательности. Дефиниция, если это возможно, не должна содержать в определяющем выражении отрицательных признаков. Однако это требование не всегда осуществимо, поэтому в некоторых случаях допустимы исключения.
4 Правило ясности и точности. Дефиниция должна быть ясной, то есть имена, используемые в определяющем выражении должны иметь четкий смысл, и среди них не должно быть метафор, сравнений и других образных выражений. При нарушении данного правила возникает ошибка «неясная дефиниция». Дефиниция должна раскрывать содержание посредством четко мыслимых признаков. При нарушении данного правила возникает ошибка «определение неизвестного через неизвестное».
В повседневной разговорной практике словарный запас языка обычно используется на интуитивном уровне. Подобная ситуация в силу наличия у людей различной интуиции часто ведет к взаимному недопониманию и даже недоразумениям. Поэтому существует насущная потребность в уточнении значений терминов. Именно эту функцию и выполняют определения, посредством которых термины получают некоторую однозначную стандартную трактовку.
Особенно велико значение четкой и однозначной терминологии в научных исследованиях, где вопросу об определениях уделяется пристальное внимание. Определения являются неотъемлемым элементом научных теорий, так как позволяют сформировать четкий понятийный и терминологический каркас этих систем знания. Они широко используются в процессе построения доказательств теоретических положений, установлении отношений между различными теориями и так далее. При этом для решения различных научных задач одному и тому же термину могут ставиться в соответствие различные смыслы. Так, в повседневной практике смысловые трактовки используемых собеседниками терминов часто строго фиксируются только на момент ведения [аргументативной] беседы и не более того, поскольку именно в аргументативных процессах чрезвычайно важна согласованность «полей аргументации» оппонентов, и прежде всего — смысловых трактовок используемых ими терминов. И даже в сфере науки, где терминам стремятся придать устойчивые, фиксированные смыслы, нередко возникают ситуации, которые требуют уточнения или переопределения уже ранее определенных терминов. Последнее является следствием постоянного развития и уточнения научного знания, в соответствии с чем трансформируются и определения научных терминов.
Всякое определение, независимо от целей и способов его введения, представляет собой констатацию наличия соответствия между языковым выражением и его смыслом. Такого рода констатации всегда являются конвенциями (соглашениями) об употреблении некоторого термина. Поэтому определения не являются предложениями и им нельзя приписывать свойства «быть истинным» или «быть ложным». Можно лишь говорить о том, выполняет ли то или иное определение свою функцию, достигает или не достигает поставленных целей.
Вау!! 😲 Ты еще не читал? Это зря!
Исследование, описанное в статье про дефиниция, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое дефиниция, инфиниция
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Логика


Комментарии
Оставить комментарий
Логика
Термины: Логика